11.Метод искусственного базиса в симплекс-методе.

В каждое уравнение, дающее отрицательную компоненту в базисное решение, нужно ввести искусственную переменную, которая имеет тот же знак, что и коэффициент в правой части уравнения. Все введённые искусственные переменные делаем базисными.

В результате

Если в оптимальном решении все искусственные переменные равны нулю, то есть минимум.

Если y₁ = … = y_k = 0, т.е. minM(y₁+…+y_k) = 0 => T_max = F_max

В задачах на минимум наоборот

Если хотя бы одна из искусственных переменных отлична от нуля в оптимальном решении, исходная система ограничений несовместна и ЗЛП не имеет решения.

12.Двойственные задачи линейного программирования.

Задача 1

Задача 2

Такие задачи называются двойственными.

Если одна из взаимодвойственных задач имеет оптимальное решение, то оптимальные значения в этих задачах равны:

Приведём эти задачи к каноническому виду.

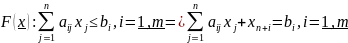
Установим соответствие между исходными переменными исходных задач и дополнительными переменными.

1 задача

Исходные: x₁,x₂…x_n

Дополнительные: x_n+1…x_n+m

2 задача

Исходные: y₁,y₂…y_m

Дополнительные: y_m+1…y_m+n

Положим ненулевым компонентам оптимального решения одной из взаимодвойственных задач соответствующие нулевые компоненты другой задачи.

Аналогично:

13.Антогонистические матричные игры. Примеры игр: поиск, игра на уклонение, типа дуэли. Максимин и минимакс. Выигрыши двух игроков.

(простейшая статическая модель). Множества стратеги двух игроков конечны и выигрыш 1 равен проигрышу 2ого. (игра с нулевой суммой)

Пусть имеются 2 игрока: А и В, и имеют n стратегий:

A: a1 a2 a3….an; n= 1, 2, 3,..N

B: b1 b2 b3…bn; n=1 2 3…N

Обозначим через aij выигрыш игрока А, при выбранной стратегии Ai, B выбрал стратегию Bj.

– матрица платежей. Данной матрицей описываются все антогонистические игры.

Примеры игр:

1. Игра «поиск»

Игрок А может прятаться в одном из двух объектов 1,2, игрок В ищет игорока А и если находит получает штраф 1у.е. , в противном случае платит игроку А 1 у.е.

Необходимо поострить ПМ

Т.к. игрок А может выбрать одну из 2 стратегий, игрок В отвечает тоже 2мя стратегиями:

В1 В2

P=

2. Игра на уклонение

Игроки 1 и 2 выбирают целые числа между 1 и n, при этом игрок 1 выигрывает величину |i—j|.

3. Дискретная игра типа дуэли

Задачами дуэльного типа описывается, например, борьба двух игроков, каждый из которых желает совершить некое единовременное действие и выбирает для этого время. Пусть игроки продвигаются навстречу друг другу на n шагов. После каждого сделанного шага игрок может выстрелить или не выстрелить в противника. Выстрел может быть у каждого только один. Считается, что вероятность попасть в противника, если продвинуться на k шагов, равно k/n. Стратегия игрока 1(2) заключается в принятии решения стрелять на i-ом(j-ом) шаге. Пусть i<j, первый игрок стреляет на i-ом шаге, а игрок 2 – на j-ом шаге. Тогда выигрыш a_ij игрока 1 задается формулой:

Таким образом, выигрыш – это разность вероятностей поражения противника и собственного выживания в дуэли. В случае i>j первым стреляет игрок 2 и a_ij = -a_ji. Если i=j, то полагаем a_ij = 0.

– нижняя цена игры или максимин – гарантированный выигрыш игрока А(если А придерживается максиминной стратегии, то ему при любом поведении противника гарантирован выигрыш, не меньше нижней цены игры).

– верхняя цена игры или минимакс – гарантированный проигрыш игрока B(если B придерживается минимаксной стратегии, то ему при любом поведении противника гарантирован проигрыш не больше верхней цены игры).

Если А придерживает максиминой стратегии, а В – минимаксной, то это принято называть принципом минимакса: .