- •№1. Основные понятия теории принятия решений. Основные модели и методы тпр. Основные этапы процесса пр. Основные понятия теории принятия решений
- •Основные модели и методы тпр.- ????
- •№2. Классификация задача принятия решений.
- •№ 4. Постановка задач линейного программирования(лп). Примеры, различные задач и подходы решения.
- •2. Транспортная задача
- •3. Игра с нулевой суммой
- •Множества решений неравенств, уравнений и их систем в задачах линейного программирования. Допустимые решения. Допустимые базисные решения.
- •№6. Сведения из теории выпуклых множеств. Выпуклые множества в н-мерном пространстве.
- •Тогда точка м (x1… xn) является выпуклой линейной комбинацией м1,…мк:
- •Множество точек выпукло, если оно вместе с произвольными 2 своими точками содержит произвольную выпуклую линейную комбинацию.
- •№7. Задача линейного программирования в канонической форме. Основные теоремы о множествах оптимальных решений этой задачи.
- •8.Геометрический метод решения злп mxn. Пример для задачи mx2 (на минимум и максимум)
- •9.Аналитический метод решения злп mxn (симплекс-метод). Для задач на минимум и максимум.
- •10.Симплекс-таблицы в симплекс-методе для задач на максимум и минимум
- •11.Метод искусственного базиса в симплекс-методе.
- •12.Двойственные задачи линейного программирования.
- •13.Антогонистические матричные игры. Примеры игр: поиск, игра на уклонение, типа дуэли. Максимин и минимакс. Выигрыши двух игроков.
- •14.Ситуация равновесия в игре. Понятие седловой точки. Чистые стратегии двух игроков.
- •15. Смешанные стратегии двух игроков в матричной игре. Выигрыши игроков в игре. Теорема Дж. Фон Неймана о ситуации равновесия.
- •16. Аналитическое решение игры 2х2. Геометрическое решение игры 2x2.
- •17. Лемма о масштабе. Условия эквивалентности смешанных стратегий двух игр.
- •18. Свойства оптимальных смешанных стратегий в матричной игре.
- •19. Графический метод решения матричной игры (2xm)
- •20. Графический метод решения матричной игры (nx2)
- •21. Активные (существенные) стратегии игроков. Теоремы об активных стратегиях.
- •22.. Принцип доминирования стратегий 2х игроков. Теоремы о доминируемых стратегиях.
- •23.. Вполне смешанная игра. Решение матричной игры n*n методом обратной матрицы.
- •24.. Сведение матричной игры n*m к двойственной задаче линейного программирования. Общий подход. Методика решения матричной игры n*m симплекс-методом.
- •25.. Принятие решения в условиях полной неопределённости. Виды неопределённостей. Критерии Байеса, Лапласа, Вальда, Сэвиджа, Гурвица, Ходжа-Лемана, мм-кртерий.
- •26.. Планирование эксперимента в статистических играх в условиях неопределённости.
- •27.. Принятие решения в условиях полной определённости. Типы задач и критериев. Классификация и общая схема решения.
- •28.. Методы решения многокритериальных задач принятия решения. Нормализация критериев.
- •29. Методы равномерной оптимальности, справедливого компромисса, свертывания критериев (аддитивный критерий), главного критерия, идеальной точки, последовательных уступок.
- •30. Принятие решений в условиях риска. Метод ожидаемого значения. Этапы принятия решений. Деревья решений.
- •31. Биматричные неантагонистические игры. Постановка задачи. Функции выигрышей.
- •32. Примеры биматричных игр: борьба за рынки, дилемма узников, семейный спор, студент-преподаватель.
- •33. Принципы доминирования в биматричных играх. Пример для матриц размера 3x3.
- •34. Ситуация равновесия по Нэшу в биматричной игре в произвольной размерности. Свойства ситуаций равновесия. Теорема Дж. Нэша. Ситуация в игре называется ситуацией равновесия по Нэшу, если
- •35. Ситуация равновесия по Нэшу в биматричной игре 2x2. Поиск смешанных стратегий для двух игроков.
- •36. Графическая интерпретация решения в биматричной игре 2x2 по Нэшу.
- •39. Позиционные игры. Дерево принятия решений. Виды позиционных игры.
- •40. Нормализация позиционной игры. Привести пример для двухходовой двухпозиционной игры с полной информацией.
- •41. Сведение позиционной игры к матричной в условиях неполной информации. На примере двухходовых и трехходовых игр.
- •42. Сведение позиционной игры к матричной в условиях полной информации о стратегиях соперника.
33. Принципы доминирования в биматричных играх. Пример для матриц размера 3x3.
Для
игрока А стратегия x’(строго) доминирует
x’’, если HA(x’,y)
(>)
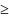 HA(x’’,y),
HA(x’’,y),
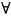 y. Для игрока B: y’(строго) доминирует
y’’, если HB(x,y’)
(>)
HB(x,y’’),
x.
y. Для игрока B: y’(строго) доминирует
y’’, если HB(x,y’)
(>)
HB(x,y’’),
x.
HA(x,y)=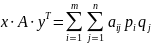
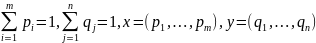
HA(x,y)=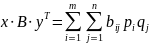 Пример:
A=
Пример:
A=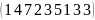 B=
B=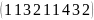 A=
B=
A=
B=
A=
B=
A=
B=
A= B= A= B=
34. Ситуация равновесия по Нэшу в биматричной игре в произвольной размерности. Свойства ситуаций равновесия. Теорема Дж. Нэша. Ситуация в игре называется ситуацией равновесия по Нэшу, если
Ситуацией равновесия
называется такая ситуация, при которой
по отдельности каждому из игроков
невыгодно отклонятся от этой
ситуации.
Ситуация(x*,y*) называется
ситуацией равновесия в смешанных
стратегиях БИ, если
x,y:
HA(x,y*)
HA(x*,y*)
и HB(x*,y)
HB(x*,y*).
Т.е. если один из игроков отклоняется
от своей равновесной стратегии, то его
выигрыш не увеличивается.
Теорема
Нэша: в БИ всегда существует хотя бы
одна ситуация равновесия в смешанных
стратегиях.
Свойства ситуации
равновесия:
1) Чтобы (x*,y*) была ситуацией
равновесия необходимо и достаточно,
чтобы
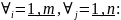

2) Пусть (x*,y*) –
ситуация равновесия, тогда, если
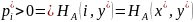 и если
и если
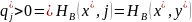
35. Ситуация равновесия по Нэшу в биматричной игре 2x2. Поиск смешанных стратегий для двух игроков.
A: x=(p1,p2)=(p,1-p),
p1=p,
p2=1-p
, B: Y=(q1,q2)=(q,1-q),
q1=q,
q2=1-q
HA(x,y)=HA(p,q),
HB(x,y)=HB(p,q)
HA(p,q)=a11pq+a12p(1-q)+a21(1-p)q+a22(1-p)(1-q),
HB(p,q)=b11pq+b12p(1-q)+b21(1-p)q+b22(1-p)(1-q)
HA=(a11-a12-a21+a22)pq+(a12-a22)p+(a21-a22)q+a22,
HB=(b11-b12-b21+b22)pq+(b12-b22)p+(b21-b22)q+b22
C=a11-a12-a21+a22,
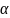 =a22-a12,
D= b11-b12-b21+b22,
=a22-a12,
D= b11-b12-b21+b22,
 =b22-b12
HA(p,q)=Cpq-
p+(a21-a22)q+a22,
HB(p,q)=Dpq-
q+(b12-b22)p+b22
=b22-b12
HA(p,q)=Cpq-
p+(a21-a22)q+a22,
HB(p,q)=Dpq-
q+(b12-b22)p+b22

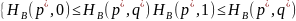 (p*,q*)-ситуация
равновесия в БИ, x*=(p*,1-p*), y*=(q*,1-q*),
HA(p*,q*)=vA,
HB(p*,q*)=vB
(p*,q*)-ситуация
равновесия в БИ, x*=(p*,1-p*), y*=(q*,1-q*),
HA(p*,q*)=vA,
HB(p*,q*)=vB
36. Графическая интерпретация решения в биматричной игре 2x2 по Нэшу.
 =>
=>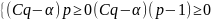
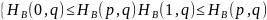 =>
=>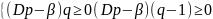 Решение
для игрока А:
1) Если p=0, то
q
Решение
для игрока А:
1) Если p=0, то
q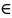 [0,1]:
Cq-
[0,1]:
Cq-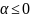 ;
2) Если p=1, то
;
2) Если p=1, то
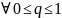 :
Cq-
:
Cq-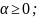 3) Если 0<p<1, то
3) Если 0<p<1, то
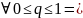 Cq-
Cq- .
Частные случаи для коэффициентов C и
1)
Если C=
=0,
=> p
[0,1],
q
[0,1],
то решением является весь единичный
квадрат. 2) Если C=0,
.
Частные случаи для коэффициентов C и
1)
Если C=
=0,
=> p
[0,1],
q
[0,1],
то решением является весь единичный
квадрат. 2) Если C=0,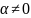 =>
либо p=0, либо p=1, т.е. решение в чистых
стратегиях. 3) C >0, то: 1. Если p=0, q
=>
либо p=0, либо p=1, т.е. решение в чистых
стратегиях. 3) C >0, то: 1. Если p=0, q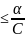 ;
2. Если p=1,
;
2. Если p=1,
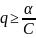 ;
3. Если 0<p<1, q=
;
3. Если 0<p<1, q=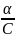 4) C <0, то: 1. Если p=0, q
4) C <0, то: 1. Если p=0, q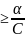 ;
2. Если p=1,
;
2. Если p=1,
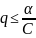 ;
3. Если 0<p<1, q=
;
3. Если 0<p<1, q=
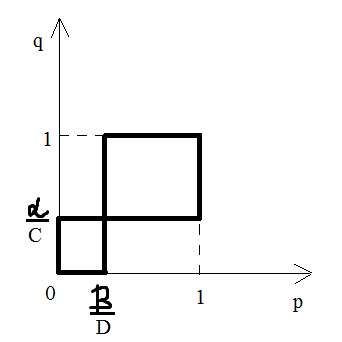
Графическая
интерпретация множества решений:
С>0
C<0
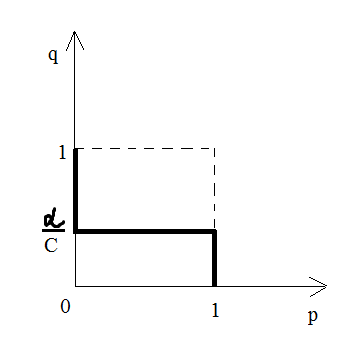

Решение для игрока
В:
1) Если q=0, то
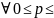 1:
Dp-
1:
Dp-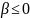 ;
2) Если q=1, то
;
2) Если q=1, то
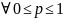 :
Dp-
:
Dp-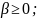 3) Если 0<q<1, то
3) Если 0<q<1, то
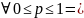 Dp-
Dp-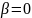 .
Частные случаи для коэффициентов D и
1)
Если D=
=0,,
то решением является весь единичный
квадрат. 2) Если D=0,
.
Частные случаи для коэффициентов D и
1)
Если D=
=0,,
то решением является весь единичный
квадрат. 2) Если D=0,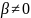 =>
либо q=0, либо q=1, т.е. решение в чистых
стратегиях. 3) D >0, то: 1. Если q=0, p
=>
либо q=0, либо q=1, т.е. решение в чистых
стратегиях. 3) D >0, то: 1. Если q=0, p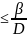 ;
2. Если q=1,
;
2. Если q=1,
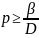 ;
3. Если 0<q<1, p=
;
3. Если 0<q<1, p=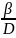 4) D <0, то: 1. Если q=0, p
4) D <0, то: 1. Если q=0, p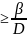 ;
2. Если q=1,
;
2. Если q=1,
 ;
3. Если 0<q<1, p=
;
3. Если 0<q<1, p=
Графическая
интерпретация множества решений:
D>0
D<0
 D>0
C>0 D<0 C>0
D>0
C>0 D<0 C>0
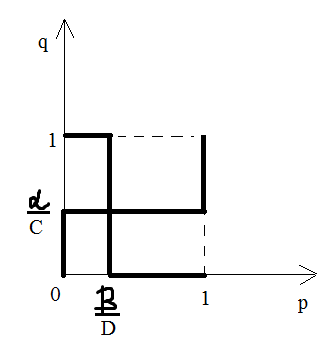 Точки
пересечения – ситуации равновесия.
(p*,q*)=(
Точки
пересечения – ситуации равновесия.
(p*,q*)=( )
)