segaee

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра Промышленной электроники (ПрЭ)

Переходные процессы

ОТЧЕТ

Индивидуальное задание

по дисциплине «Электроника и электротехника»

Студент гр. 368-1

_________С.Б. Жанаева

Старший преподаватель каф ПрЭ

_______В.Н. Башкиров

____________ «__» __ 2020

Томск 2020

Содержание

1. Индивидуальное задание…………………………………………………..3

2. Основная часть……………………………………………………………..5

Индивидуальное задание

Приведено 10 схем для расчета.

Номер варианта состоит из трех цифр.

Первая цифра – номер схемы (Номера приведены слева и обведены)

Вторая цифра - номер строки с параметрами индуктивностей и емкостей в таблице 1

Третья цифра – номер строки с параметрами сопротивлений и источников ЭДС в таблице 2

В таблицах приводится больше данных, чем необходимо для схемы, поэтому выбираются только необходимые параметры.

Содержание задания у всех одинаковое.

Для заданных линейной электрической цепи и её параметров рассчитать и построить кривые переходных процессов тока и напряжения на накопителях энергии (конденсаторах и ёмкостях).

Отчет по выполнению ИЗ должен включать:

- составленная схема, согласно заданию;

- расчет граничных значений для схемы (ННУ, ЗНУ, КУ);

- расчеты классическим методом;

- расчеты операторным методом;

- построение и сравнение временных характеристик напряжения и тока на накопителях энергии, полученные в разных методах расчета;

- выводы по результатам расчета.

Для расчетов можно применять различные математические пакеты.

R1, Ом	R2, Ом	R3, Ом	L1, Гн	L4, Гн	C3, мкФ	E, В
40	8	30	0,2	0,1	25	120

2 Основная часть

1. Расчёт граничных значений

1.1. Независимые начальные условия.

Рисунок 2.1 - Схема и направления токов до коммутации

Рассчитаем значения токов при времени t = 0-

Ток i3 = 0, так как ток на конденсаторе при наших условиях не протекает, отсюда следует, что в данной схеме все остальные токи равны между собой.

Рассчитаем значение напряжений при t = 0-

1.2. Зависимые начальные условия.

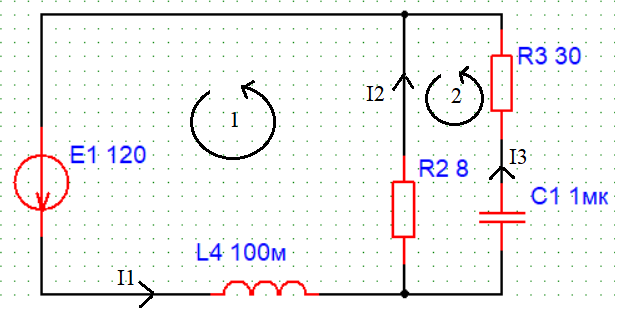
Рисунок 2.2 – Схема, токи и обход контуров после коммутации

По законам коммутации:

I_L(0-)= I_L(0+)= I₁(0-)

U_c(0-) = U_c(0+)

Составим систему уравнений по первому и второму закону Кирхгофа, для нахождения токов. По первому закону у нас будет 1 уравнение, так как у нас 2 узла, по второму закону у нас будет 2 уравнения, так как мы имеем 2 контура.

Найдём значения токов и напряжений при t = 0+

i1-i2-i3=0;

R2*i2+U_L = E;

R3*i3-R2*i2+U_c = 0;

Вычислим значения токов и напряжения на катушке, подставив значения в матрицу

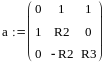
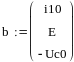
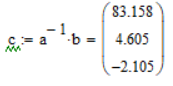
1.3. Конечные условия

Рисунок 2.3 – Схема после коммутации.

Рассчитаем значения токов и напряжений при t =∞

так как переходный процесс прошёл и ток на конденсаторе стал равен нулю

Найдём напряжение на конденсаторе:

2. Найдём корни характеристического уравнения, методом входного сопротивления:

В электротехнике доказано, что характеристическим уравнением является числитель входного сопротивления ЭТЦ после коммутации, найденного в операторной форме.

3. Расчёт значений классическим методом:

3.1. Расчёт значений для конденсатора:

где A1, A2 – постоянные интегрирования;

p1, p2 – корни характеристического уравнения, которые были рассчитаны ранее

Определим постоянные интегрирования, взяв систему уравнения, при t=0:

Подставим значения в матрицу и найдём постоянные интегрирования:

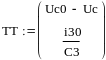
Составим уравнения для напряжения и тока:

В конечном виде получим зависимости тока от времени и напряжения от времени, для конденсатора:

Uck(t)=120 + 89.221*exp(-10³*t) + (-99.221)*exp(-81.412*t)

Ick(t) = 25*10^-6*(120 + 89.221*exp(-10³*t) + (-99.221)*exp(-81.412*t))d/dt

3.2. Расчёт значений для катушки индуктивности:

где B1, B2 – постоянные интегрирования;

p1, p2 – корни характеристического уравнения, которые были рассчитаны ранее.

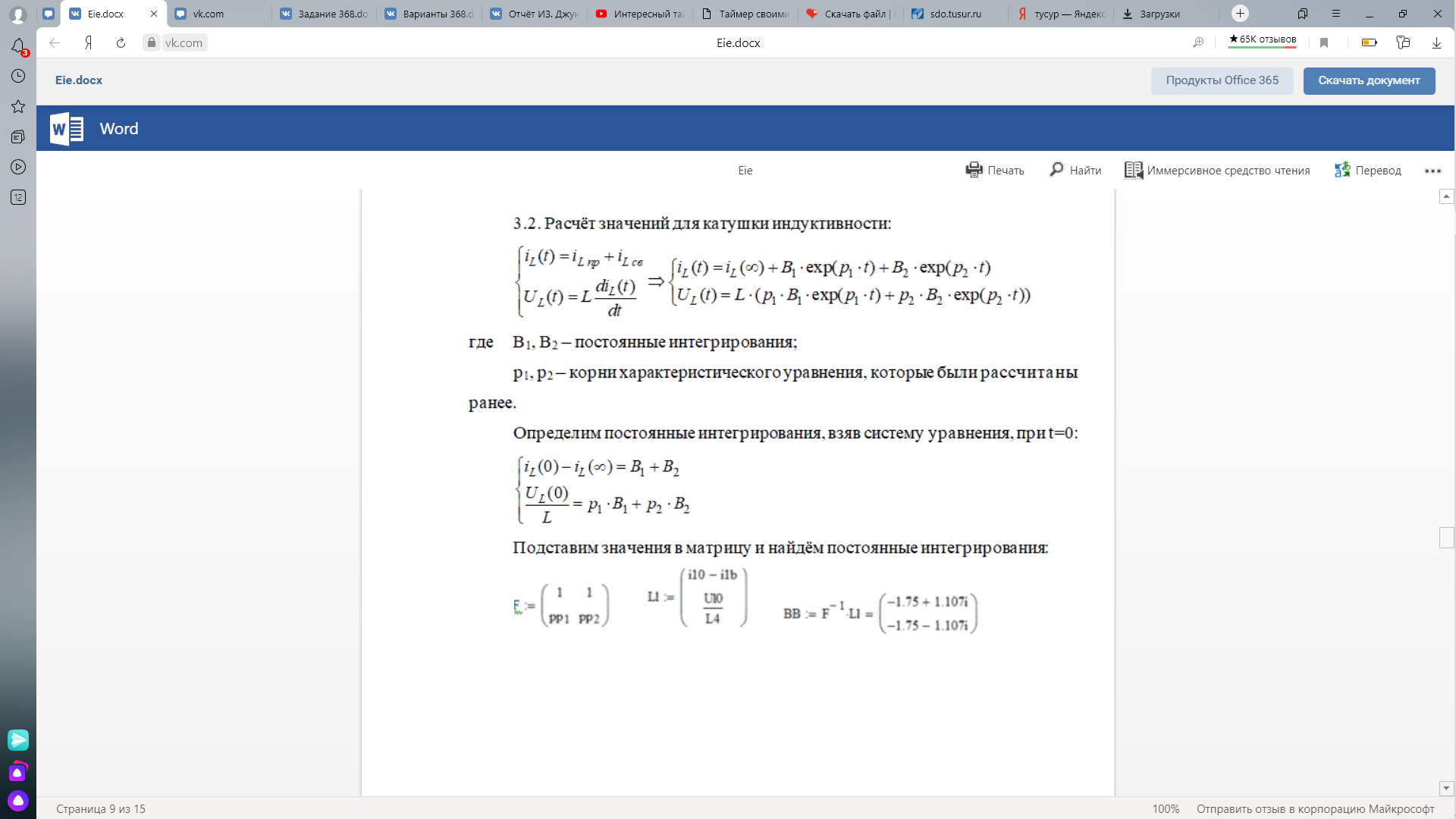
Определим постоянные интегрирования, взяв систему уравнения, при t=0:

Подставим значения в матрицу и найдём постоянные интегрирования:

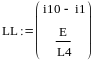
Составим уравнения для напряжения и тока:

В конечном виде получим зависимости тока от времени и напряжения от времени, для катушки индуктивности:

Ilk(t) = 15 – 0.191*exp(-10³*t) – 12.309* exp(-81.412*t)

Ulk(t) = 0.1*(15 – 0.191*exp(-10³*t) – 12.309* exp(-81.412*t))d/dt

4. Расчёт значений операторным методом:

Рисунок 2.4 – схема, токи, обходы контуров, для расчёта операторным методом

По законам Кирхгофа составим уравнения

Составим матрицу для решения системы

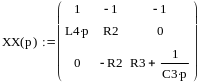
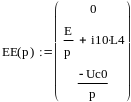
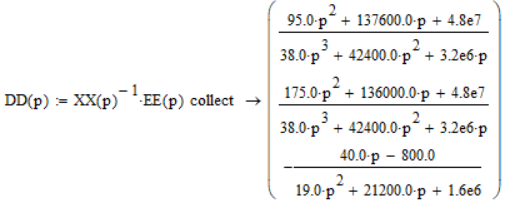
Возьмем знаменатель вида B(p) для решения характеристического уравнения

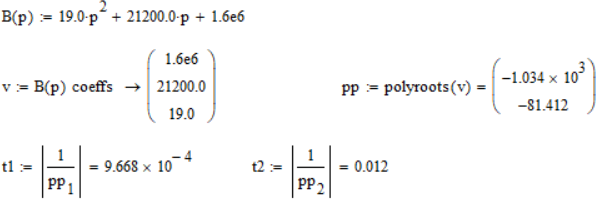
Корни характеристического уравнения совпали, с корнями, найденными методом входного сопротивления.

Возьмём время переходного процесса, как 5 наибольших постоянных времени:

Для дальнейшего решения найдём производную от характеристического уравнения:

Запишем напряжение на конденсаторе и напряжение на катушке индуктивности, как функции от изображения, вида F(p):

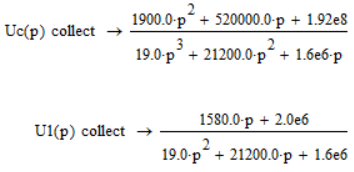
Составим функции числителей для токов и напряжений:

Составим функции переходного процесса для токов и напряжений, перейдя от изображения к оригиналу:

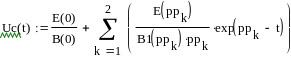
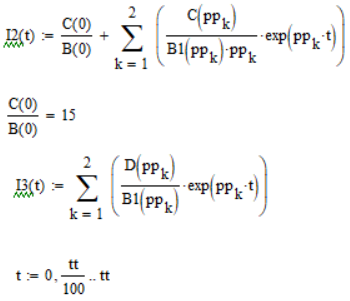
Зависимости токов и напряжений, полученные операторным методом, совпадают с зависимостями, рассчитанными классическим методом.

5. Построение и сравнение временных характеристик напряжение и тока, разными методами вычисления

На рисунке 2.5 представлены графики сравнения напряжений на конденсаторе и катушке индуктивности, рассчитанные классическим методом и операторным методом:

Рисунок 2.5 – изменение напряжений со временем протекания переходного процесса.

Из графика видно, что изменения напряжений, рассчитанные классическим и операторным методами, совпали, следовательно, результаты измерений верны.

На рисунке 2.6 представлены графики сравнения токов, рассчитанные классическим методом и операторным методом:

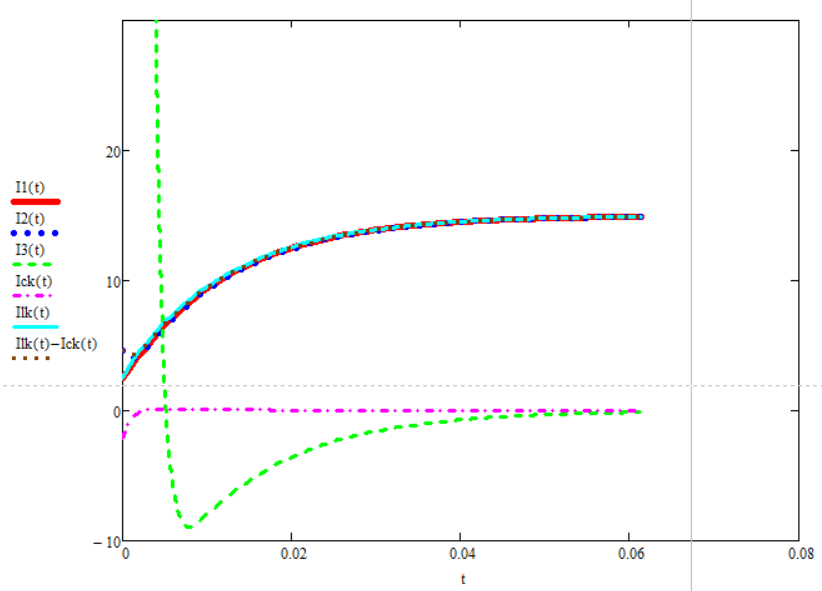
Рисунок 2.6 – изменение токов со временем протекания переходного процесса

График тока i3 в классическом методе представлен как разница токов на катушке и конденсаторе, по первому закону Кирхгофа.

Из графика видно, что изменение тока, рассчитанное классическим методом, совпадает с изменением тока, рассчитанным операторным методом, из этого следует, что расчёты верны.