LR1_OTH_backup
.docxМинистерство образования и науки
Российской Федерации
Федеральное государственное бюджетное образовательное
учреждение высшего профессионального образования
ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ
СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)
Кафедра промышленной электроники (ПрЭ)
Лабораторная работа № 1
Моделирование и
исследование характеристик типовых
динамических звеньев систем автоматического
управления
Студент гр. 368-1
____________ В.В.Никифоров
Научный руководитель:
___________ Ю.М.Лебедев
Томск 2020
Задание
Исходные данные для индивидуального варианта:
Вариант |
k |
T, с |
20 |
2 |
0,12 |
1. Исследование инерционного (апериодического) звена
Рисунок 1 – Модель инерционного звена
1.1.
Собрать схему модели апериодического
(инерционного) звена (рис. 1), установить
значения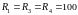
кОм. По формулам
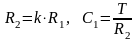рассчитать параметры остальных элементов
в соответствии с исходными данными для
индивидуального варианта.
1.2.
Напряжение питания источника принять
равным
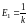В.
1.3.
Получить переходную характеристику и
опреде-лить время переходного процесса
.
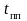1.4.
Получить экспериментальные ЛАЧХ и
ЛФЧХ, замерить частоту среза
и значение фазы
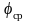на этой частоте.
1.5. Увеличить значения постоянной времени Т звена в два, три, и четыре раза и повторить выполнение заданий по п.п. 1.3 и 1.4.
1.6.
Построить графики зависимосте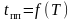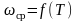й
,
и
.
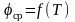1.7. Оценить влияние величины постоянной времени на характеристики апериодического (инерционного) звена.
2. Исследование инерционного форсирующего (упругого) звена
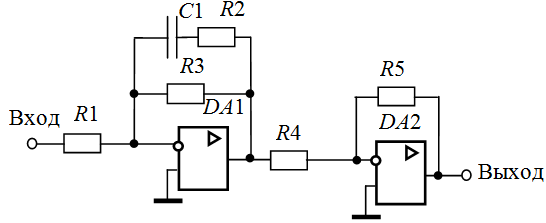
Рисунок 2 – Модель инерционного форсирующего звена
2.1.
Собрать схему электронной модели
инерционного форсирующего (упругого)
звена (рис. 2). Принять
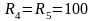кОм,
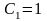мкФ. Для заданного варианта из табл.
4.1
выбрать значение постоянной времени
,
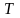принять постоянную времени и коэффициент
передачи звена
.
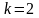По формулам
,
,
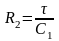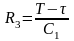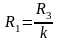рассчитать параметры остальных элементов
модели. Напряжение
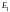источника питания электронной модели
принять равным 0,5 В.
2.2.
Снять переходную характеристику и
определить величину скачка
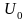переходной характеристики при
,
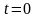установившееся значение
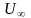и время переходного процесса
.
Рассчитать параметр
.
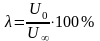2.3. Получить экспериментальные ЛАЧХ и ЛФЧХ, замерить частоту среза и значение фазы на этой частоте.
2.4.
Установить соотношения значений
постоянных времени
,
,
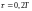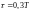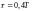и повторить выполнение заданий п.п. 2.2
и 2.3, пересчитав параметры модели в
соответствии с п. 2.1.
2.5.
Построить графики зависимостей
,
,
,
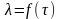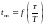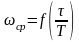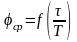и сравнить их с аналогичными зависимостями,
полученными в п. 1.5.
2.6. Оценить влияние постоянной времени инерционного форсирующего звена на его характеристики.
3. Исследование звеньев второго порядка
Рисунок 3 – Модель второго порядка
3.1.
Собрать схему модели звена второго
порядка в соответствии с рис. 3. Приняв
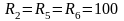кОм,
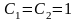мкФ,
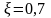и, выбрав значения постоянной времени
и коэффициента передачи
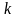согласно индивидуальному варианту,
рассчитать значения остальных параметров
модели по формулам:
,
,
.
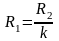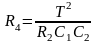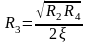3.2.
Установить напряжение питания модели,
равное
,
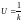снять переходную характеристику и
определить время переходного процесса
,
фиксируя при этом осциллографом
максимальное
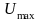значение выходного напряжения.
3.3. Рассчитать перерегулирование
,
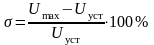где
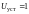В. При правильном расчете параметров
электронной модели колебательного
звена перерегулирование не должно
превышать 5%.
4.3.4.
Получить экспериментальные ЛАЧХ и
ЛФЧХ, замерить частоту среза
,
значение фазы
на
частоте среза и определить запас
устойчивости по фазе
.
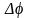3.5.
Установить значения
,
,
,
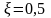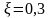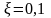а также
,
,
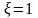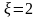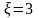и повторить выполнение п.п. 4.3.2 – 4.3.4.
3.6.
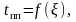
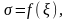
Построить графики зависимосте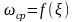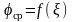й
,
и
.
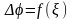3.7. Оценить влияние коэффициента демпфирования на характеристики звеньев второго порядка.
Выполнение
1. Исследование инерционного (апериодического) звена
1.1 Экспериментальная модель
1.2 Номиналы элементов и параметры звена
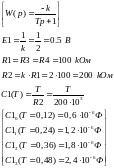
1.3 Осциллограммы
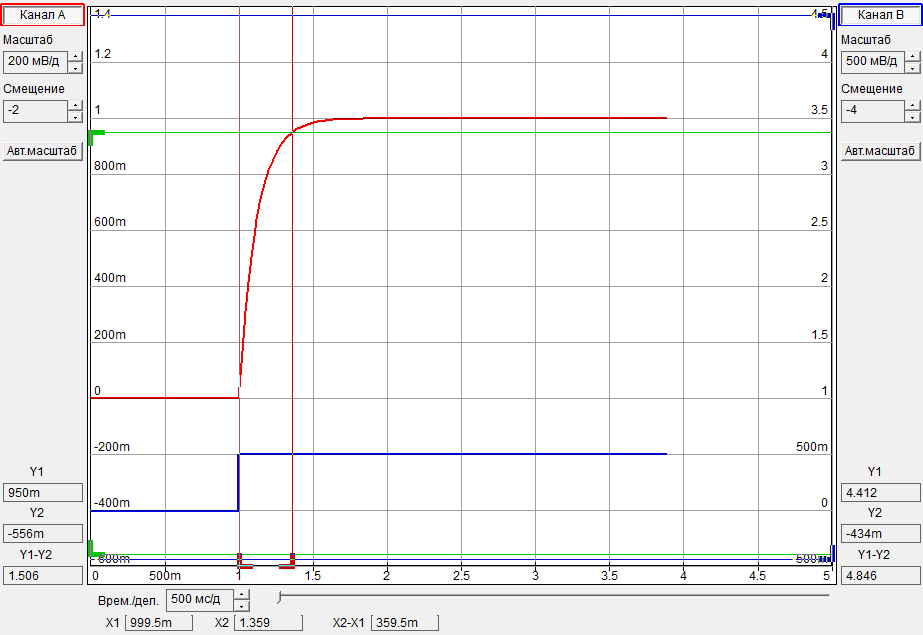
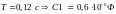
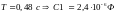
1.4 Графики Боде
1.5 Исследование зависимостей
1.5.1 Таблица полученных значений
T, c |
∆t, c |
fср, Гц |
ωср, рад/с |
φ,° |
0,12 |
0,36 |
2,292 |
14,394 |
-60 |
0,24 |
0,72 |
1,150 |
7,226 |
-60 |
0,36 |
1,1 |
0,766 |
4,813 |
-60 |
0,48 |
1,45 |
0,575 |
3,613 |
-60 |
1.5.2 Графики зависимости
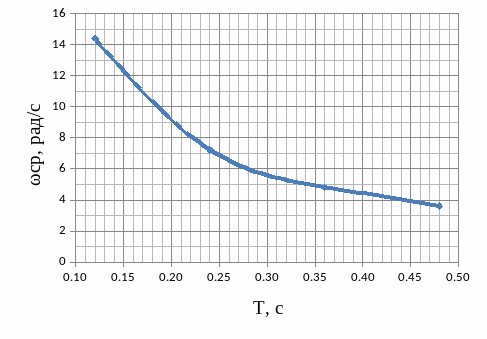
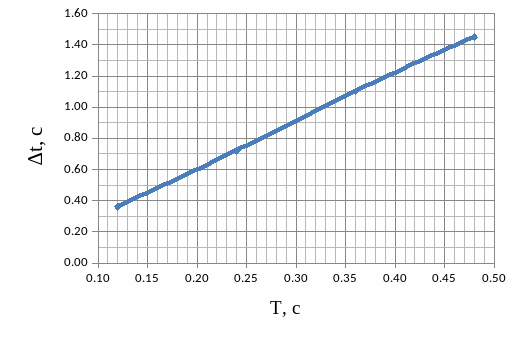
1.6 Краткий анализ
При увеличении постоянной времени T инерционного звена:
А) Время переходного процесса ∆t линейно возрастает, из за чего система дольше переходит в стационарный режим;
Б) Частота среза уменьшается по экспоненциальному закону, что уменьшает область устойчивости системы.
2. Исследование инерционного форсирующего (упругого) звена
2.1 Экспериментальная модель
2.2 Номиналы элементов и параметры звена
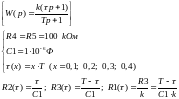
τ(x), c |
R1(τ), Ом |
R2(τ), Ом |
R3(τ), Ом |
0,012 |
5,4∙104 |
1,2∙104 |
10,8∙104 |
0,024 |
4,8∙104 |
2,4∙104 |
9,6∙104 |
0,036 |
4,2∙104 |
3,6∙104 |
8,4∙104 |
0,048 |
3,6∙104 |
4,8∙104 |
7,2∙104 |
2.3 Осциллограммы
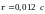
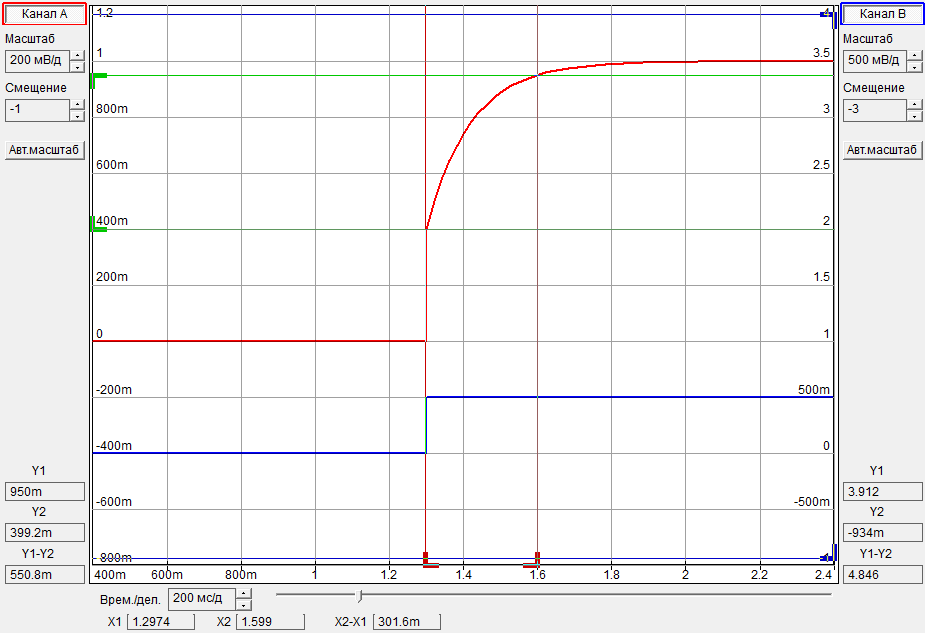
2.4 Графики Боде
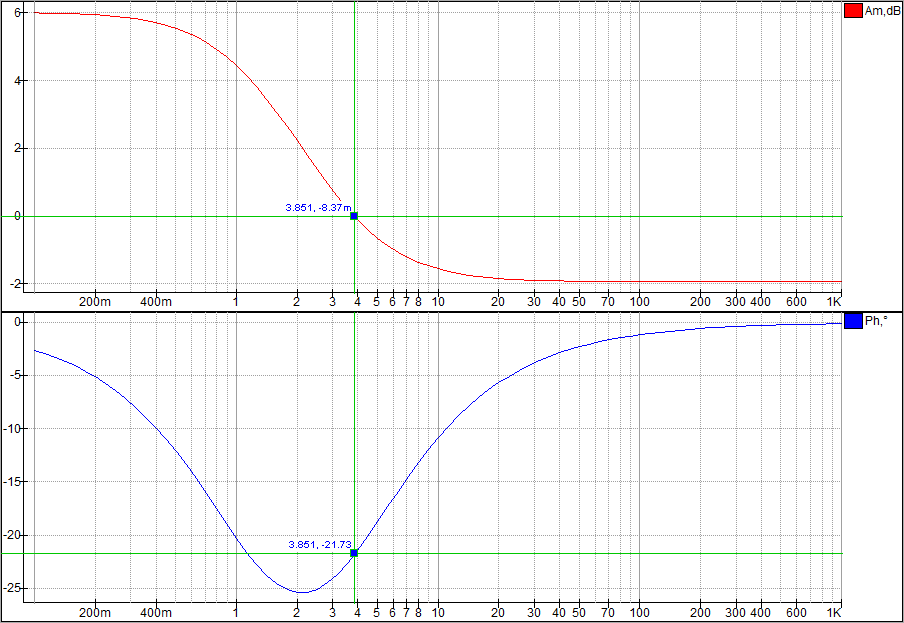
2.5 Исследование зависимостей
2.5.1 Таблица полученных значений
τ(x), c |
λ, % |
∆t, c |
ωср, рад/с |
φср,° |
0,012 |
10 |
0,348 |
14,753 |
-50 |
0,024 |
20 |
0,335 |
15,758 |
-41 |
0,036 |
30 |
0,318 |
18,070 |
-32 |
0,048 |
40 |
0,302 |
24,102 |
-21 |
2.5.2 Графики зависимости
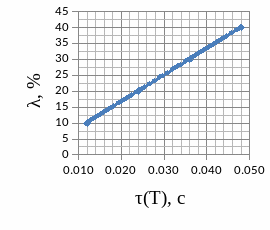
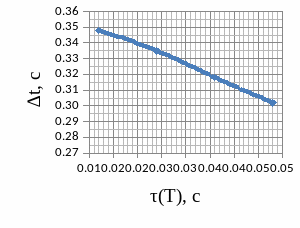
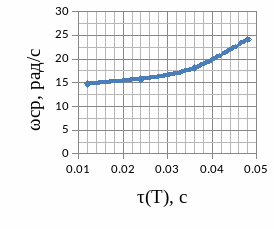
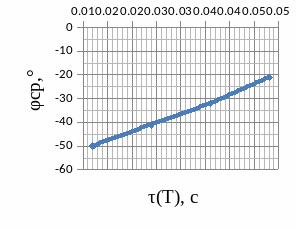
2.6 Краткий анализ
При линейном увеличении постоянной времени τ:
А) ЛАЧХ системы не меняется, но смещается вверх, за счет этого меняются значения частоты и фазы среза;
Б) ЛФЧХ системы становится менее крутой, поэтому значения фазы среза растут, несмотря на смещение частоты среза через минимум в виде параболы;
В) Резкий скачок напряжения вначале переходного процесса линейно увеличивается.
Г) Время ПП слабо уменьшается, т.к. зависит от начального скачка напряжения.
3. Исследование звеньев второго порядка
3.1 Экспериментальная модель
3.2 Номиналы элементов и параметры звена
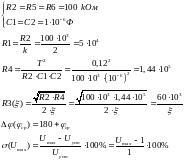
ξ |
0,1 |
0,3 |
0,5 |
1 |
2 |
3 |
R3(ξ), Ом |
6∙105 |
2∙105 |
1.2∙105 |
6∙104 |
3∙104 |
2∙104 |
3.3 Осциллограммы
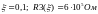
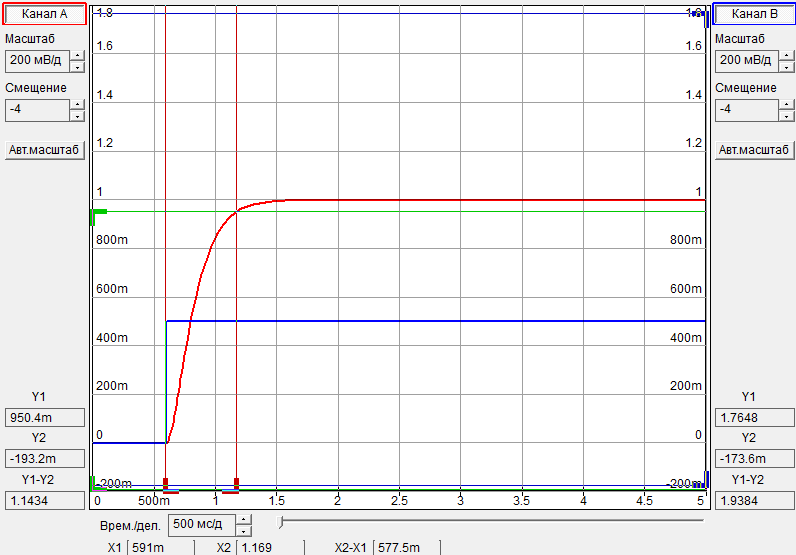
3.4 Графики Боде
3.5 Исследование зависимостей
3.5.1 Таблица полученных значений
ξ |
∆t, c |
ωср, рад/с |
φср,° |
σ, % |
∆φ,° |
Umax,В |
fср, Гц |
0,1 |
3,500 |
14,407 |
-170 |
72,7 |
10 |
1,727 |
2,293 |
0,3 |
1,250 |
13,779 |
-150 |
37,2 |
30 |
1,372 |
2,193 |
0,5 |
0,648 |
12,673 |
-130 |
16,5 |
50 |
1,165 |
2,017 |
1 |
0,578 |
8,332 |
-90 |
0 |
90 |
1 |
1,326 |
2 |
1,390 |
3,833 |
-67 |
0 |
113 |
1 |
0,610 |
3 |
2,133 |
2,476 |
-63 |
0 |
117 |
1 |
0,394 |
3.5.2 Графики зависимостей
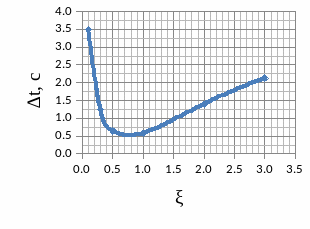
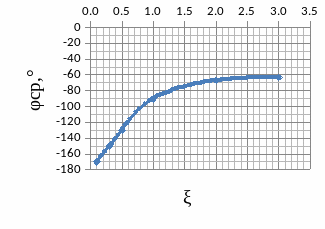
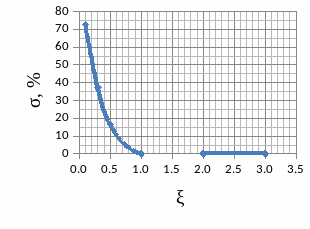
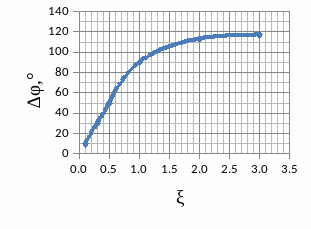
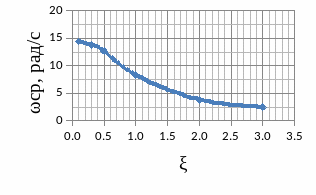
3.6 Краткий анализ
При изменении ξ от 0 до 1:
А) Время ПП уменьшается экспоненциально;
Б) Показатель перерегулирования также убывает по экспоненциальному закону;
В) Переходный процесс осуществляется по гармоническому закону.
При изменении ξ от 1 до 3:
А) Время ПП начинает линейно расти;
Б) Показатель перерегулирования устанавливается на 0;
В) Переходный процесс осуществляется по апериодическому закону.
Общий анализ, при ξ от 0 до 3:
А) Фаза на срезе частот, также как и запас устойчивости по фазе растут по обратному экспоненциальному закону;
Б) ЛАЧХ также, как и ФЧХ, сглаживаются.
4. Контрольные вопросы
4.1. Как количественно величина постоянной времени связана с временем переходного процесса в инерционном звене?
4.2. Почему в инерционном звене фаза на частоте среза не зависит от постоянной времени звена?
4.3. Как изменятся характеристики инерционного форсирующего звена при и его реализация на электронной модели?
4.4. В каком случае колебательное звено становится консервативным и как при этом изменятся его характеристики?
4.5. Как нужно изменить схему, приведенную на рис. 4.4, чтобы получить электронную модель консервативного звена?
4.6. Чему равен запас устойчивости по амплитуде в звеньях второго порядка?
4.7. Чем объяснить наличие перегиба на переходной характеристике апериодического звена второго порядка?