otchet2math

Министерство науки и высшего образования РФ

Федеральное государственное бюджетное образовательное

учреждение высшего образования

ТОМСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ

СИСТЕМ УПРАВЛЕНИЯ И РАДИОЭЛЕКТРОНИКИ (ТУСУР)

Кафедра промышленной электроники (ПрЭ)

Отчет по лабораторной работе №4

по дисциплине «Метрология и технические измерения»

Выполнили студенты гр. 368-1

______Бубнов С.Б.

______Жанаева С.Б.

______Чевгунов С.Б.

Принял:

Доцент кафедры ПрЭ.

______Жаров Б.И.

Томск 2020

Цель работы

Целью лабораторной работы является углубление знаний по применению преобразования Лапласа на примере расчёта операторным методом переходных процессов в электрической цепи с нулевыми начальными условиями, содержащей два или три независимых контура с тремя накопителями энергии, моделирование процессов в этой цепи и сравнение полученных результатов.

Задание

1. Для заданного варианта работы выбрать схему электрической цепи (четырёхполюсника) и исходные данные для параметров элементов этой цепи.

2. Составить схему замещения этой цепи, произвольно выбрать направления токов в ветвях цепи и напряжений на её элементах (направления напряжений должны совпадать с направлениями токов).

3. Пользуясь законами Кирхгофа, составить систему уравнений, описывающих электрические процессы в заданной цепи.

4. Перевести полученную систему уравнений в операторную форму, заменив оригиналы токов i(t) и u(t) на их изображения I(p) и U(p) , а производную d/dt (с учётом нулевых начальных условий) – на оператор Лапласа p .

5. Для системы алгебраических уравнений, полученных в п.4, составить матрицу M(p) коэффициентов перед изображениями переменных (токов и напряжений), обратить её, возведя в степень -1, и умножить на вектор правых частей V(p).

6. С помощью символьного процессора системы MathCAD решить полученную систему Y(p)=M(p)-1 *V(p).

7. Записать в символьном виде полученные изображения переменных.

8. Записать полином знаменателя изображений переменных, относительно переменной p определить вектор коэффициентов этого полинома a . Далее вычислить вектор корней p уравнения.

9. Присвоить указанному полиному знаменателя изображение A( p), вычислить его производную.

10. С помощью теорем разложения осуществить обратное преобразование Лапласа для изображений переменных,

11. Рассчитать токи заряда конденсаторов, вычислить конечное время расчёта оригиналов.

12. Построить графики изменения токов и напряжений на накопительных элементах электрической цепи, а также её выходное напряжение.

13. Определить установившиеся значения токов и напряжений в схеме.

14. Определить максимальные и минимальные значения переменных на графике.

15. Проанализировать полученные результаты, оценив характер переходных процессов и изменения переменных.

17. Для варианта, заданного при выполнении лабораторной

работы, в программе ASIMEC изобразить электрическую схему, предусмотрев в ней шунты.

18. Поочерёдно подключая осциллограф параллельно накопительным элементам, с помощью горизонтальных маркеров измерить максимальное, минимальное и установившееся значения напряжения на этих элементах. То же самое проделать для токов в накопительных элементах, подключая осциллограф параллельно шунтам или другим резисторам.

19. Оформить таблицу с результатами измерений, сопоставить их результатами расчёта и рассчитать погрешность моделирования.

Ход работы:

1. Составим схему замещения:

Рисунок 1.1 - Схема замещения.

2. Составили систему уравнений по первому и второму закону Кирхгофа:

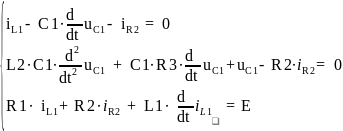
3. Перевели систему уравнений в операторную форму:

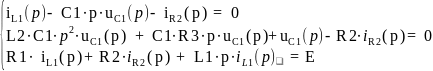
4. В MathCad составили матрицу левых и правых частей:

5. Решение методом линейной алгебры и последующее нахождение оригиналов и изображений:

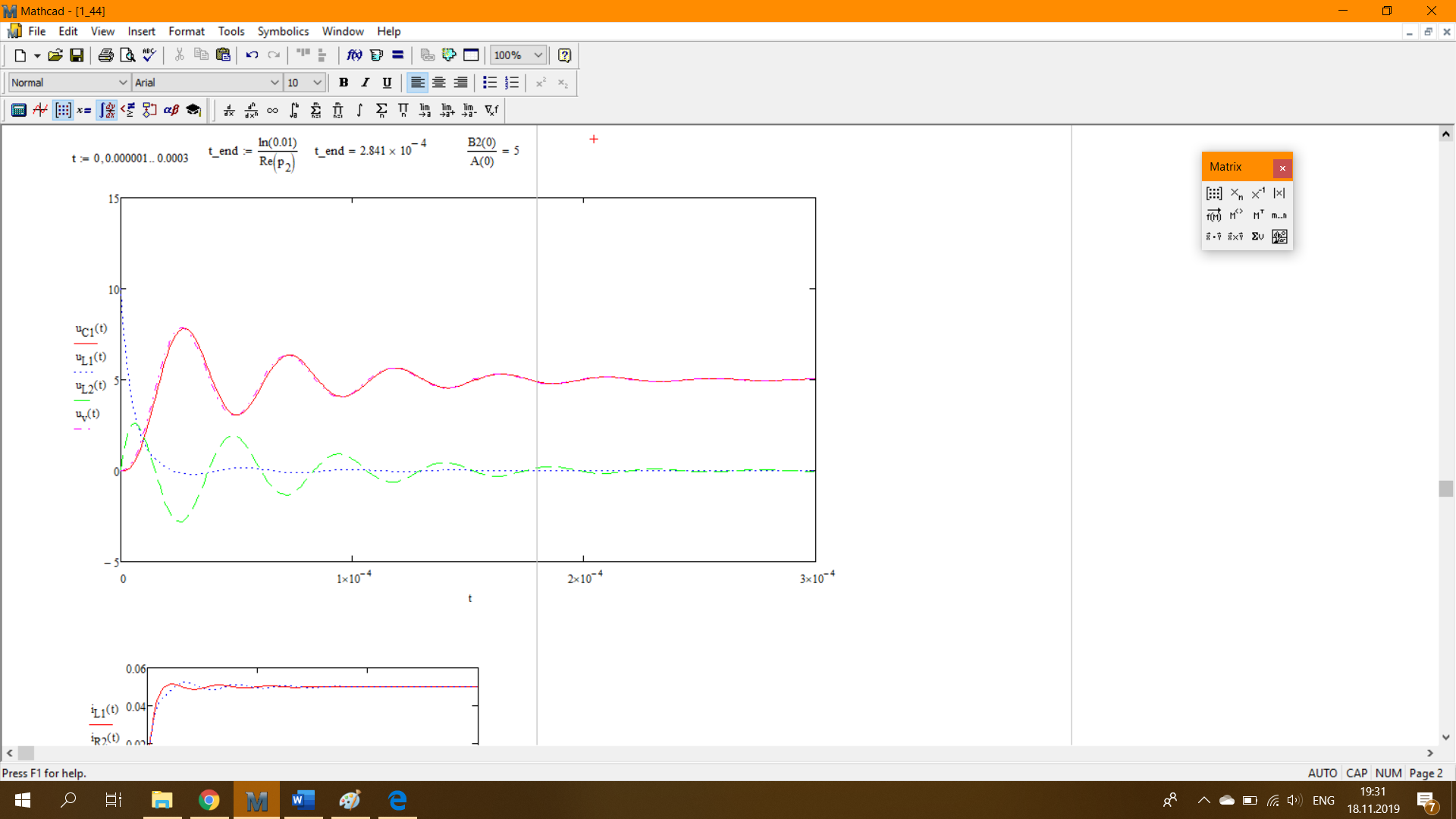
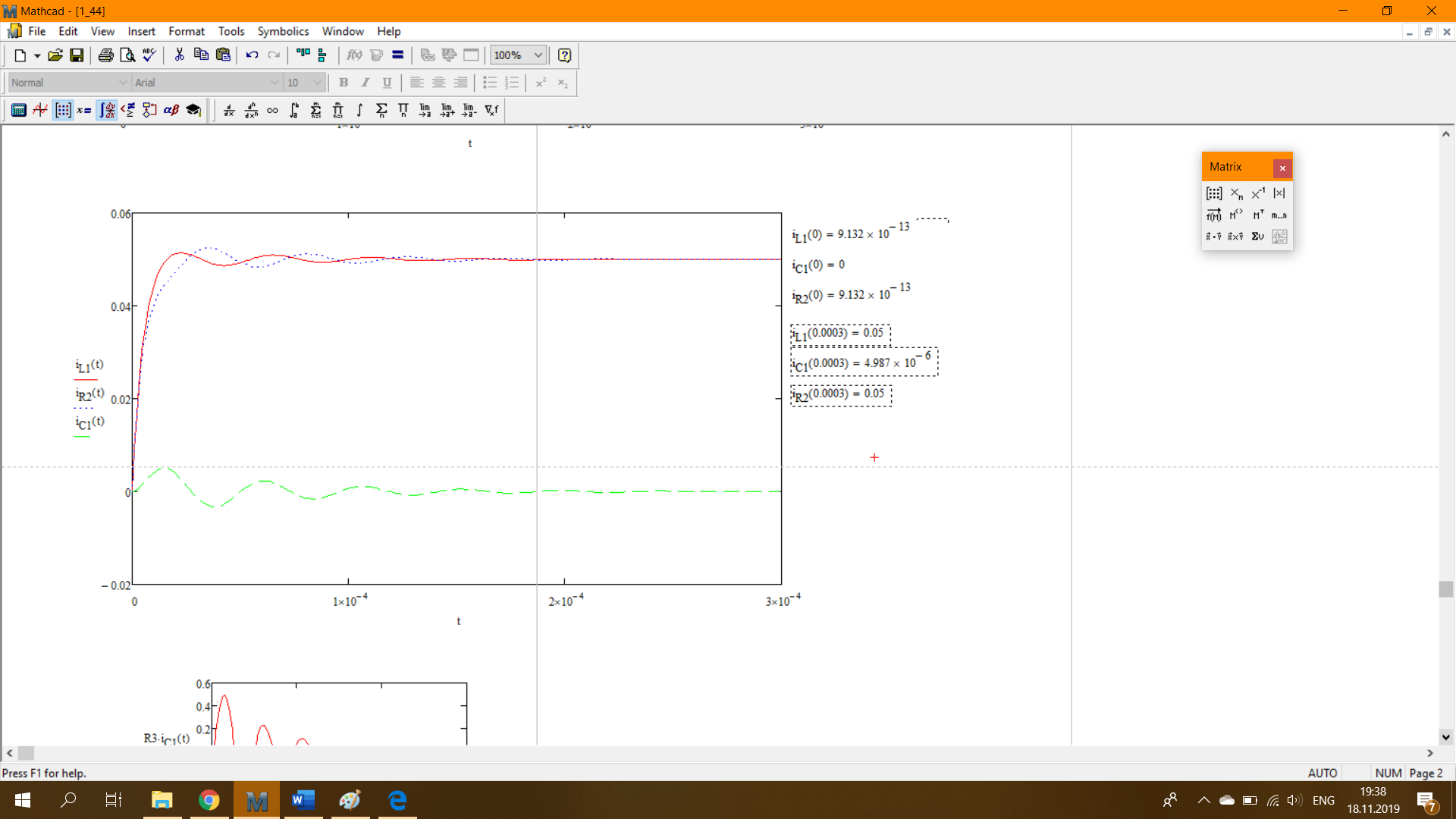
6. Моделирование в ASIMEC:

На рис. 1.2 приведены осциллограммы напряжений на конденсаторе C1. Максимальное значение напряжения измеряется с помощью верхних горизонтальных маркеров, в соответствии с которыми:

U_C1,max = 7.8 В

U_C1,min = -0.016 В

Рисунок 1.2 - Осциллограмма напряжения на конденсаторе C1.

На рис. 1.3 приведена осциллограмма напряжения на дросселе L1, в соответствии с которой:

U_L1,max = 10.028 В,

U_L1,min = -0.236 В.

Рисунок 1.3 - Осциллограмма напряжения на дросселе L1.

На рис. 1.4 приведена осциллограмма напряжения на дросселе L2, в соответствии с которой:

U_L2,max = 2.599 В,

U_L2,min = -2.83 В.

Рисунок 1.4 - Осциллограмма напряжения на дросселе L2.

На рис. 1.5 приведена осциллограмма напряжения на резисторе R1. Минимальное и максимальное значение этого напряжения:

U_R1,max = 5.131 В,

U_R1,min = 0.016 В.

тогда минимальный и максимальный ток, протекающий в R1:

I_L1,max = 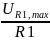= 0.0513 A,

I_L1,min = 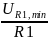= 0.0001 A.

Рисунок 1.5 - Осциллограмма напряжения на резисторе R1.

На рис. 1.6 приведены осциллограммы напряжений на резисторах R2 (верхняя осциллограмма) и R3 (нижняя осциллограмма). Максимальные и минимальные значения напряжения на них, измеренные с помощью горизонтальных маркеров:

U_R2,max = 5.258 В, U_R3,max = 0,49 В,

U_R2,min = 0.024 В, U_R3,min = -0,33 В.

тогда максимальный и минимальный ток заряда конденсаторов C1 и С2:

I_С1,max = 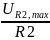= 0.0049 A, I_R2,max = 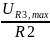= 0.0525 A,

I_С1,min = 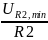= -0.0033 A, I_R2,min = = -0.0002 A.

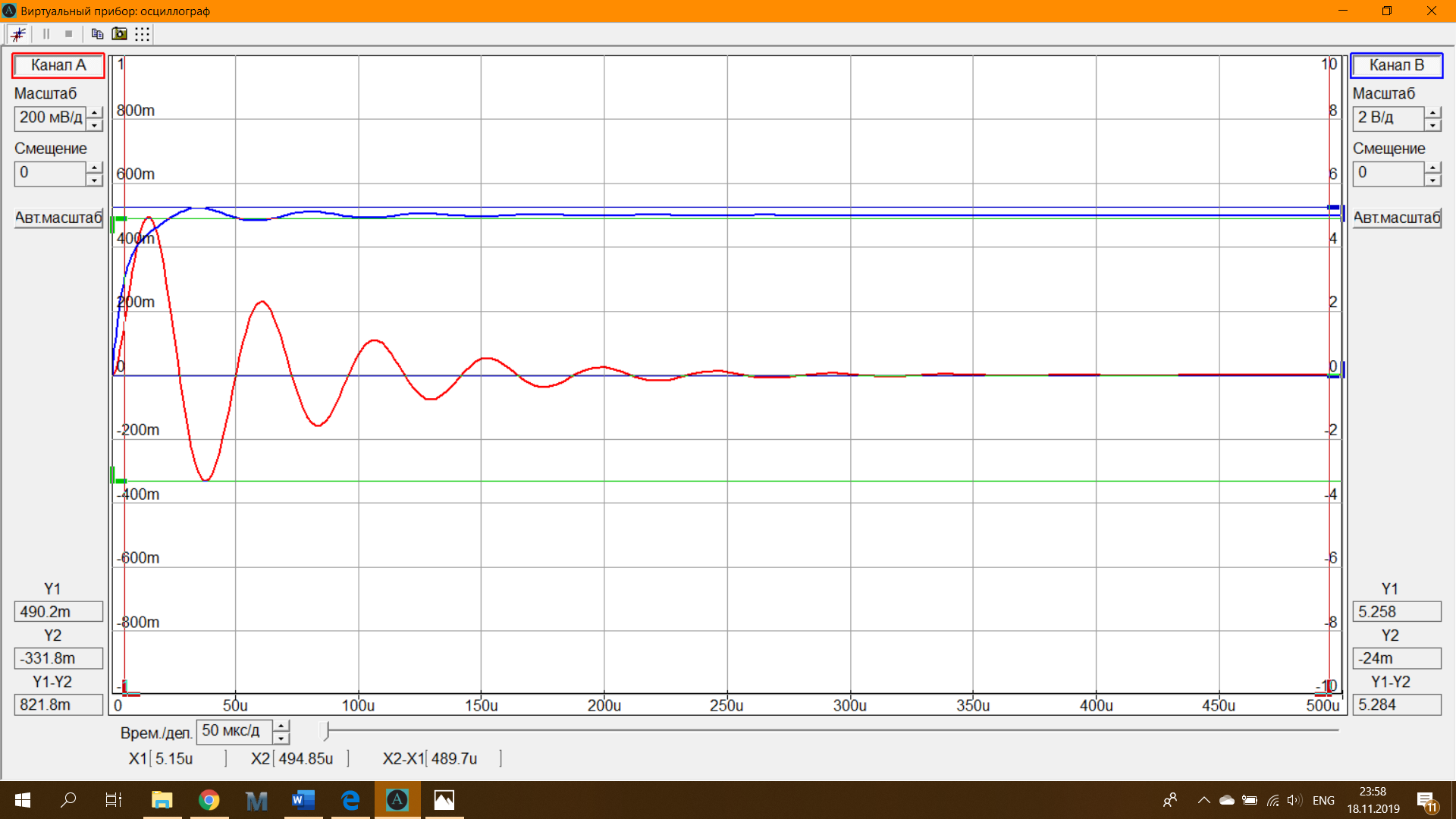
Рисунок 1.6 - Осциллограммы напряжений на резисторах R2 и R3.

7. Расчеты погрешностей

8. Таблица минимальных и максимальных значений, полученных в ходе расчёта и модуляции в ASIMEC, погрешность вычислений.

Переменная	Значения переменой
	Максимальное				Минимальное
	Расчёт	Модель	Погрешность	Расчёт		Модель	Погрешность
UС1, В	7.817	7.8	0.22	-		-0.016	-
UL1, В	10	10.028	0.28	-0.209		-0.236	11.44
UL2, В	2.603	2.599	0.15	-2.812		-2.83	0.636
IL1, А	0.0513	0.0513	0	-		0.0001	-
iС1, А	0.0049	0.0049	0	-0.0033		-0.0033	0
IR2, А	0.0523	0.0525	0.381	-		-0.0002	-

Заключение:

В основном, относительная погрешность моделирования не превысила 1 %, что является хорошим результатом. Исключение составляют только погрешности, полученные для минимальных значений токов на резисторе R2 и дросселе L1, которые обусловлены малой величиной тока.