1. Теоретическая часть

Функция, которая подвергается преобразованию Лапласа, должна обладать следующими свойствами [2, 4, 8]:

1. Функция должна быть определена и дифференцируема по всей положительной полуоси;

2. Функция должна быть тождественно равна 0 при , т.е. ( при );

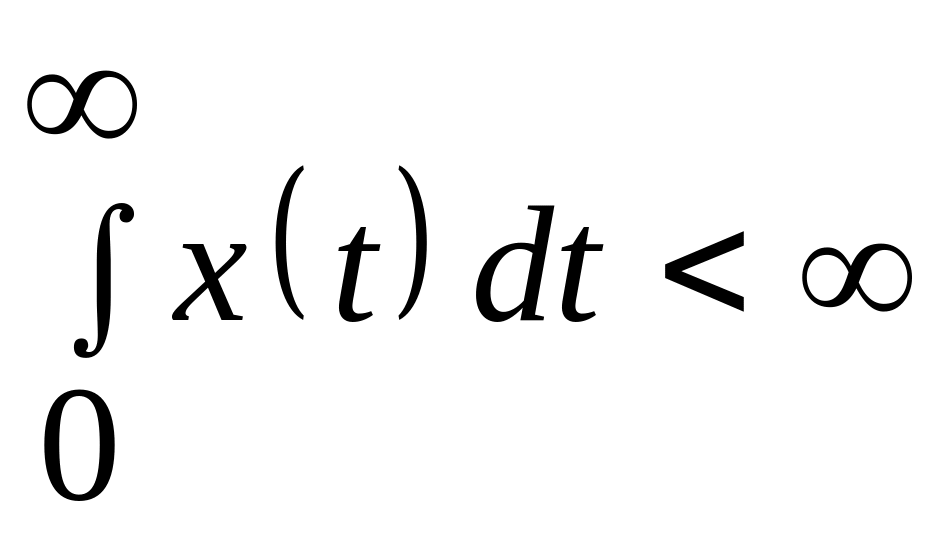
3. Функция должна быть ограниченна, т.е. для функции существуют такие положительные числа М и с, что при , т.е. , где с – абсцисса абсолютной сходимости (некоторое положительное число).

Преобразование Лапласа это соотношение вида 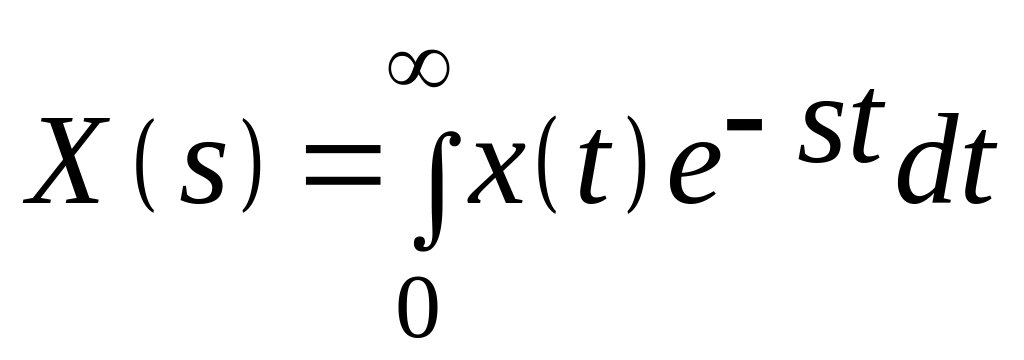, ставящее функции вещественного переменного в соответствие функцию комплексного переменного ( ).

При этом называется оригиналом, – изображением.

Символическая запись преобразования Лапласа, а именно,

, где – оператор прямого преобразования Лапласа.

1.1 Нахождение оригиналов функций по их изображениям

Если изображение функции является дробно-рациональной функцией вида

,

то нахождение оригинала производится по аналитическим формулам:

1. Для случая, когда корни простые, вещественные:

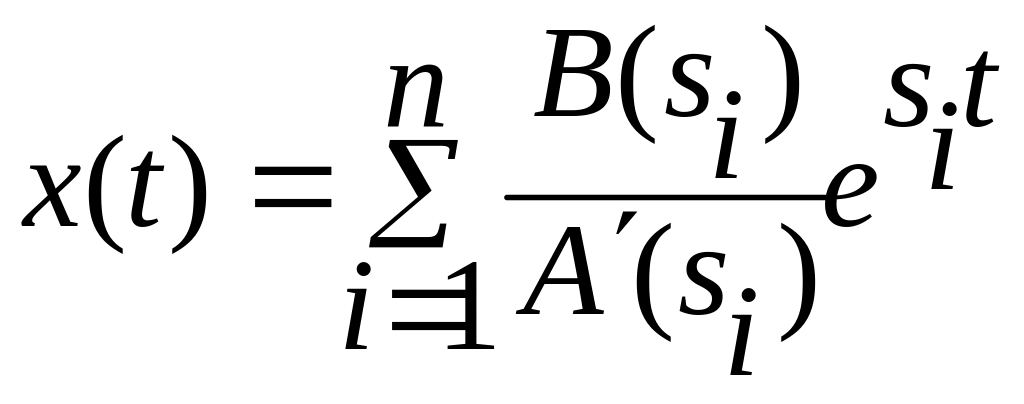. (1)

2. Для случая, когда корни простые, вещественные и один корень нулевой, т.е. :

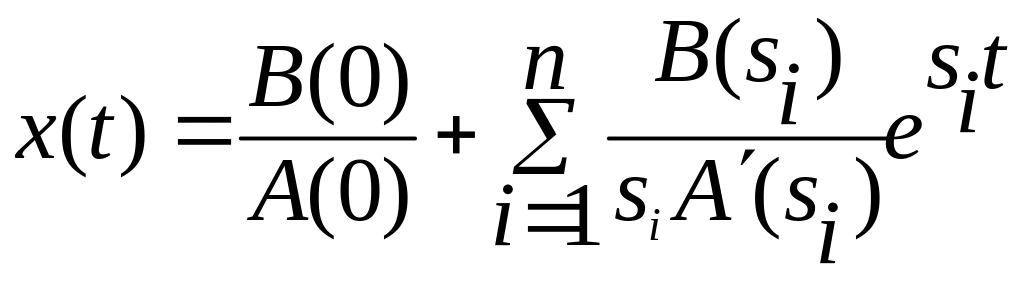. (2)

3. Для случая, когда корни комплексно-сопряженные, (считается для одного корня):

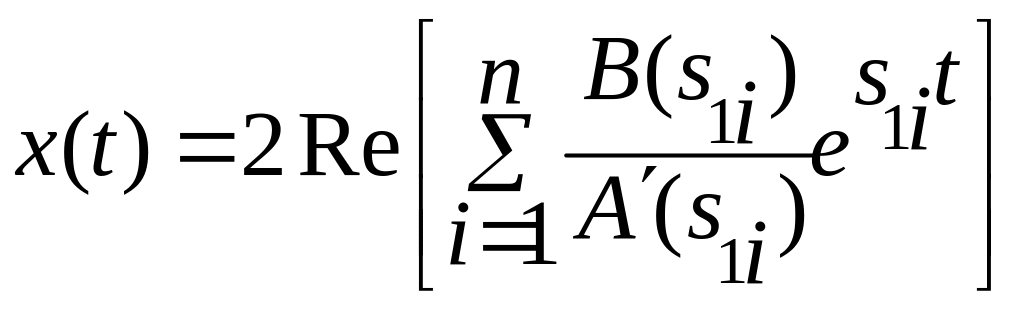, если (3)

.

4. Для случая, когда корни комплексно-сопряженные и один нулевой:

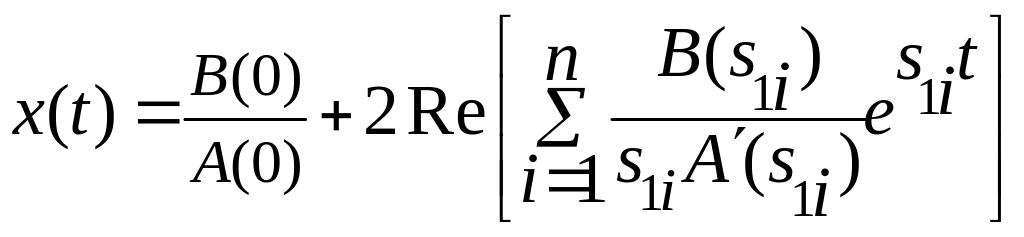. (4)

2. Практическая часть

Определим порядок вычисления оригинала функции по его изображению:

1. Вычислить корни полинома : .

Число корней равно порядку полинома .

2. Выбрать формулу для расчёта оригинала.

3. Вычислить производную .

4. Вычислить значения полиномов и при подстановке корней полинома знаменателя.

5. Вычислить значения коэффициентов при функциях .

Пример 1

.

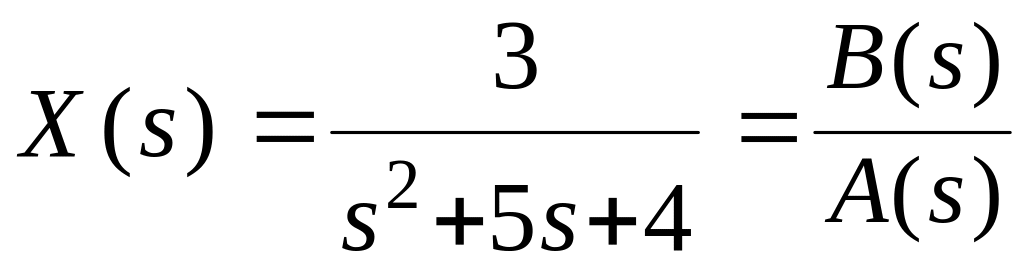1. .

2. Корни вещественные, выбираем формулу (1): .

3. Вычисляем

.

.

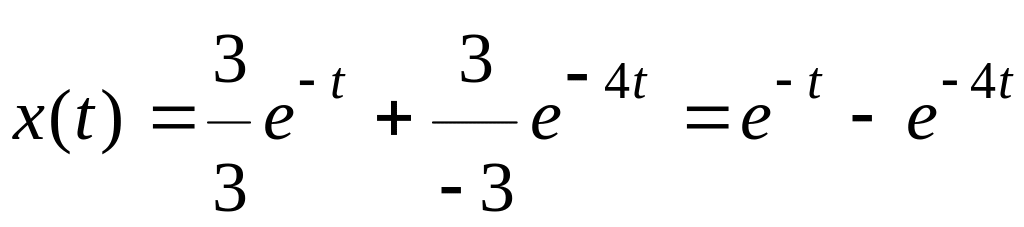Рассмотрим пример вычисления с использованием MATLAB:

>> p=[1 5 4]; - коэффициенты полинома знаменателя;

>> b=[3]; - коэффициенты полинома числителя;

>>r=roots(p) – вычисление корней знаменателя;

r =

-4

-1

>>r1=r(1); r2=r(2)

>> dp=polyder(p) – вычисление коэффициентов производной ;

dp =

2 5

>> A1=polyval(dp,r1) – вычисление для первого корня;

A1 = 3

>> A2=polyval(dp,r2) – вычисление для второго корня;

A2 = -3

>>В1= polyval(b, r1) – вычисление для первого корня;

В1=3

>> C1=В1./A1 – вычисление коэффициента при первом корне;

C1 = 1

>>В2= polyval(b, r2) – вычисление для второго корня;

В2= 3

>> C2=В2./A2 – вычисление коэффициента при втором корне;

C2 = -1

>> t=[0:0.01:5] ;– интервал времени и шаг счёта;

>> x=C1.*exp(r1.*t)+C2.*exp(r2.*t);

>> plot(t,x),grid on, xlabel('Time(sec)'), ylabel('x(t)')

На рис. 1. приведен график функции, построенный с использованием оператора plot(t,x).

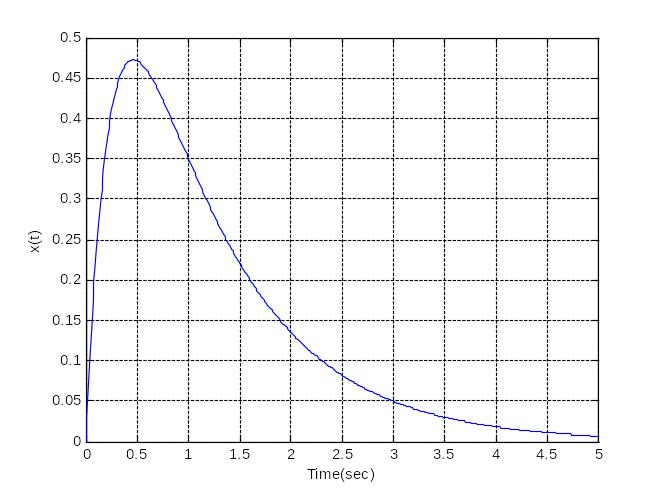
Рис. 1. График функции, построенный с использованием оператора plot(t,x)

Изображению 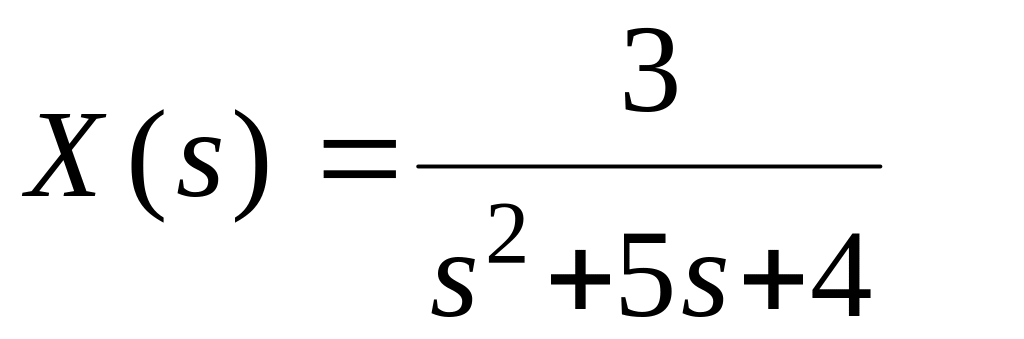соответствует оригинал .

Проверим правильность преобразований. Для этого воспользуемся предельными теоремами.

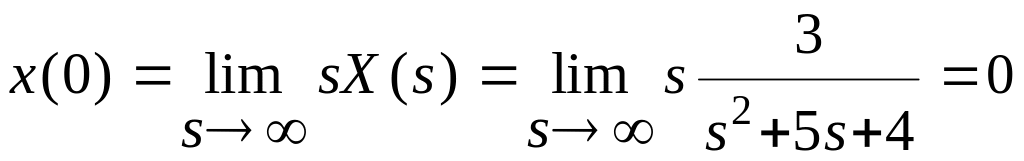
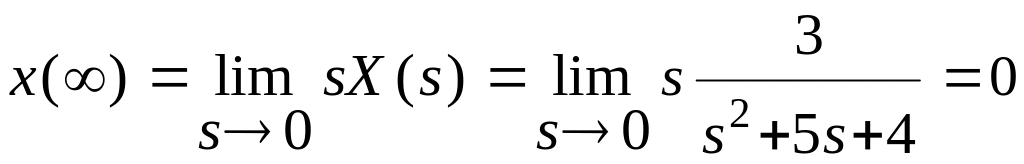
Пример 2

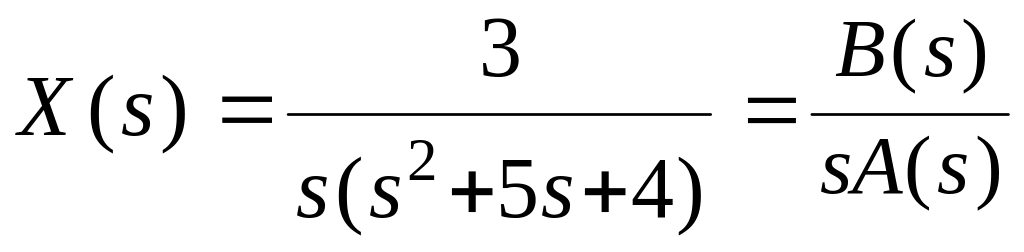
1. .

2. Корни вещественные и один нулевой, выбираем формулу (2):

.

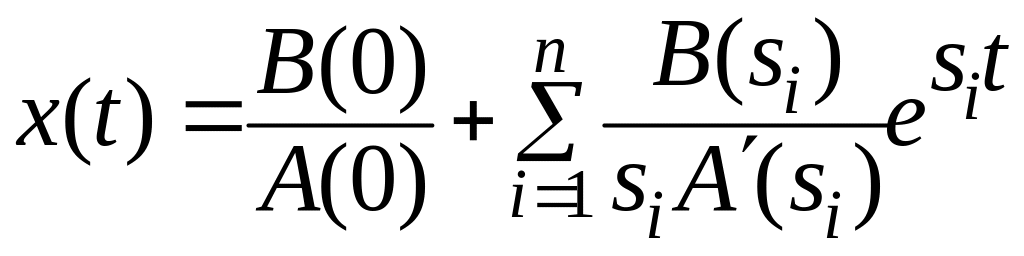3. Вычисляем

.

.

Воспользуемся результатами расчёта из примера 1 и пересчитаем коэффициенты с использованием MATLAB:

>>C3=C1./(r1) – вычисление коэффициента при первом корне;

C3 = -1

>> C4=C2./(r2) – вычисление коэффициента при втором корне;

C4 = 0.2500

>>В0= polyval(b, 0) – вычисление для нулевого корня;

В0=3

>>А0=polyval(p,0) – вычисление для нулевого корня;

А0=4

>>С0=В0./А0 – вычисление коэффициента при нулевом корне;

С0=0.75

>> x1=С0+C3.*exp(r1.*t)+C4.*exp(r2.*t);

>> plot(t,x1), grid on, xlabel('Time(sec)'), ylabel('x1(t)')

На рис. 2. приведен график функции, построенный с использованием оператора plot(t,x).

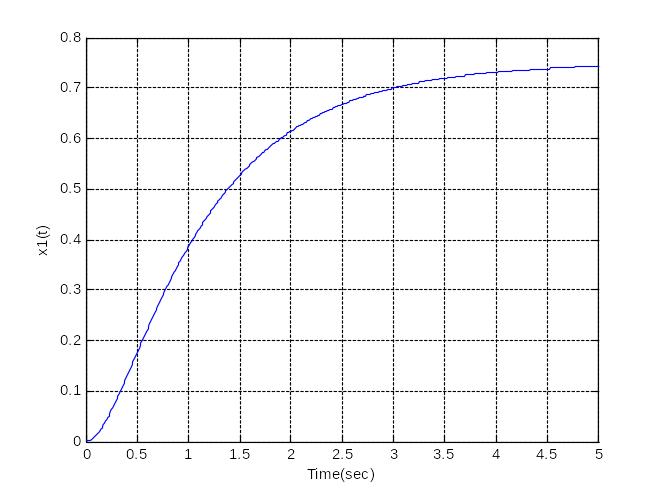
Рис. 2. График функции, построенный с использованием оператора plot(t,x)

Изображению 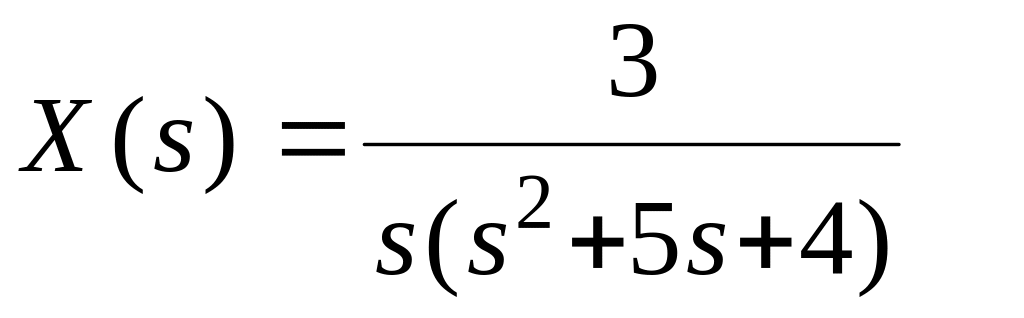соответствует оригинал .

Проверим правильность преобразований

.

.
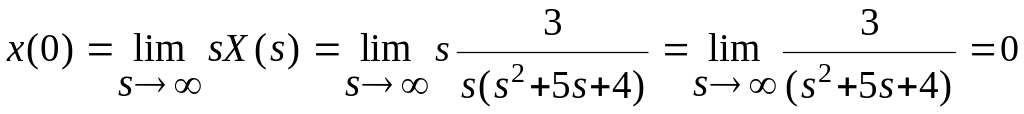
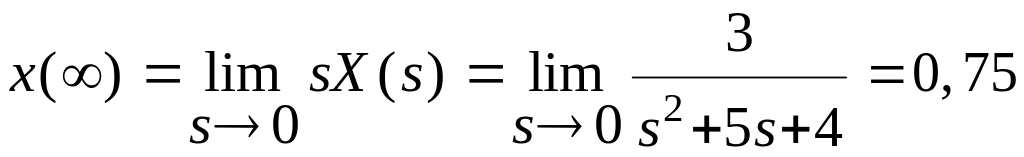