Вопросы для собеседования

1. Определение устойчивости;

2. Условия устойчивости;

3. Критерии устойчивости;

4. Критерий устойчивости Гурвица;

5. Принцип аргумента;

6. Критерий устойчивости Михайлова;

7. Критерий устойчивости Найквиста;

8. Определение устойчивости по логарифмическим частотным характеристикам; запасы устойчивости по фазе и амплитуде.

Лабораторная работа № 7 «Исследование точности линейных систем управления в установившемся режиме»

Цель лабораторной работы - формирование практических навыков по исследованию точности линейных систем управления в установившемся режиме.

Задача лабораторной работы - освоение технологии исследования точности работы линейных систем управления в установившемся режиме. Закрепление полученных знаний на практике. Экспериментальное определение ошибки системы управления при различных входных воздействиях, анализ влияния изменения структуры системы и её параметров на ошибку системы, определение коэффициентов ошибок.

Необходимое время для выполнения работы: - 2 академических часа.

Необходимые приборы и оборудование:

• Компьютер, совместимый с IBM PC, ОЗУ не менее 512 Мб.

• Операционная система WINDOWS *.

• Математический пакет MATLAB Version *.

Форма отчётности студентов: индивидуальный отчёт с типовым титульным листом и результатами моделирования.

Защита работы: собеседование с преподавателем по контрольным вопросам, выполнение индивидуальных заданий.

1. Теоретическая часть

Точность системы управления в установившемся режиме определяется величиной установившейся ошибки системы при различных входных воздействиях [1, 5, 6, 8].

Для её вычисления необходимо уметь вычислять передаточные функции с разными точками приложения воздействия и снятия сигнала.

Рассмотрим типовую одноконтурную систему управления и определим передаточные функции системы, рис. 1.

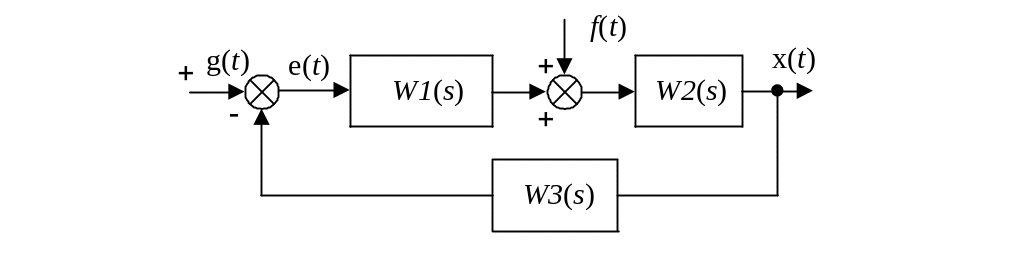
Рис. 1. Типовая одноконтурная систему управления

1. Передаточная функция замкнутой системы по задающему воздействию при ( ).

.

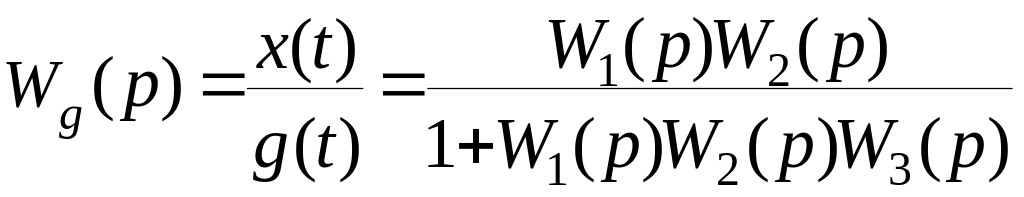2. Передаточная функция замкнутой системы по возмущению при ( )

.

.

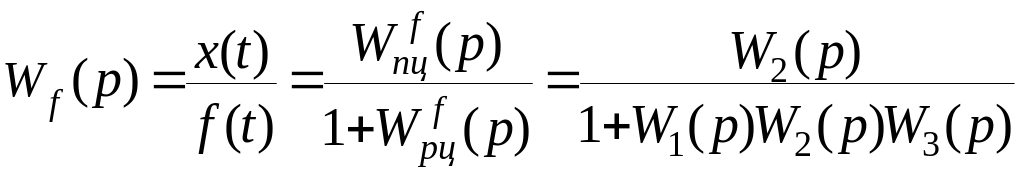3. Передаточная функция замкнутой системы по ошибке по задающему воздействию при ( ).

.

.

.

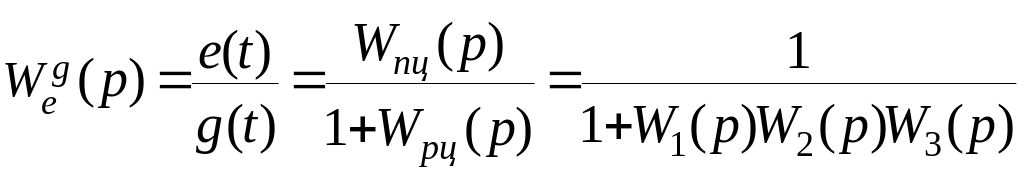4. Передаточная функция замкнутой системы по ошибке по возмущению при ( ).

Выходной сигнал будет определяться как

Рассмотрим способы определения ошибки в установившемся режиме:

Первый способ, наиболее простой, позволяет оценить ошибку системы без сложных вычислений. Он основан на использовании передаточных функций системы по ошибке и теоремы о конечном значении функции.

Пусть задана передаточная функция разомкнутой системы в виде ,. На вход системы поступают задающее воздействие g(t) и возмущение f(t). Для определения ошибки в замкнутой системе необходимо найти передаточную функцию по ошибке для соответствующего воздействия:

.

Определим точность системы при отработке задающего воздействия, для чего используем теорему о конечном значении, т.е. .

.

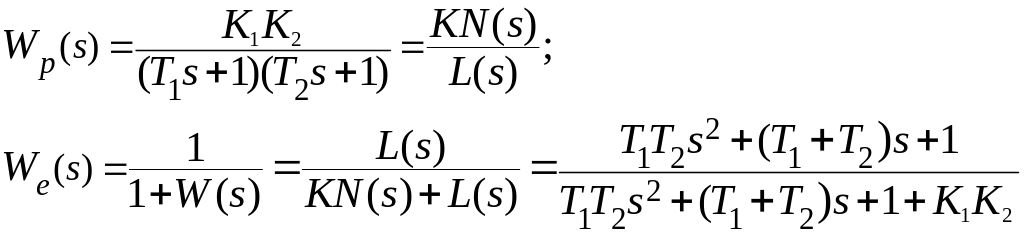
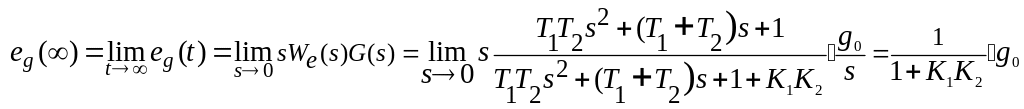Аналогично получаем .

Второй способ основан на вычислении коэффициентов ошибок.

Разложим передаточную функцию замкнутой системы по ошибке по возрастающим степеням комплексной переменной s в ряд, сходящийся при малых s.

Изображение ошибки будет иметь вид:

.

Если передаточная функция является дробно-рациональной, то разложение в ряд можно осуществить простым делением числителя на знаменатель, располагая члены полиномов в порядке возрастания степеней.

Если воздействие дифференцируемо на всем интервале от 0 до , то ошибка системы может быть представлена в виде ряда

или

Коэффициенты называются коэффициентами ошибок системы.

- коэффициент статической или позиционной ошибки, – коэффициент скоростной ошибки, – коэффициент ошибки от ускорения.

В статических системах все коэффициенты ошибок не равны нулю.

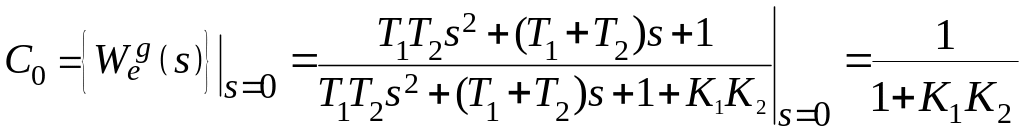
В системах с астатизмом 1 порядка – .

.

.

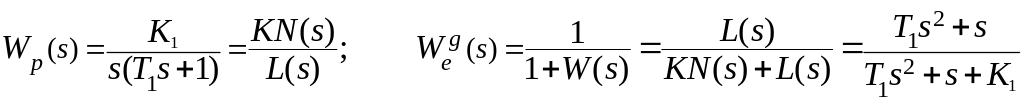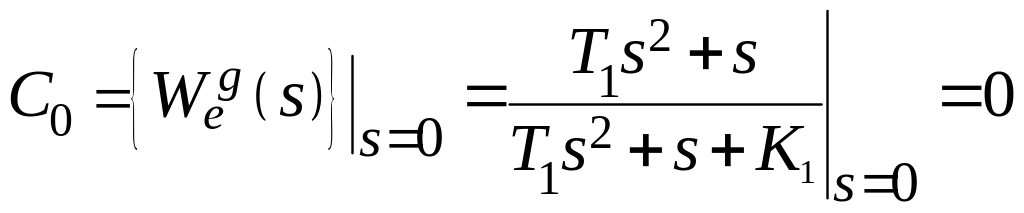Коэффициенты ошибок позволяют легко определить, как будет изменяться ошибка системы при подаче на вход различных видов воздействий. Поэтому исследование коэффициентов ошибок позволяет наметить пути уменьшения или полного устранения установившейся ошибки.