Содержание отчёта
1. Цели и задачи и выводы лабораторной работы.
2. Эквивалентные передаточные функции систем, полученные при последовательном и параллельном соединении звеньев, соединениях с обратной связью, выполненных самостоятельно и при помощи функций series, parallel и feedback.
3. Выводы по содержанию и результатам лабораторной работы.
Вопросы для собеседования
Какая система называется разомкнутой, замкнутой?
Какую систему называют одноконтурной, многоконтурной?
Дайте определение прямой цепи, разомкнутой цепи?
Какие связи называются перекрещивающимися (перекрёстными)?
Как определить передаточную функцию многоконтурной замкнутой системы?
Лабораторная работа № 4 «Временные характеристики линейных систем управления. Определение реакции системы на произвольное входное воздействие»
Цель лабораторной работы - формирование практических навыков по нахождению временных характеристик линейных систем управления.
Задача лабораторной работы - освоение технологии нахождения временных характеристик линейных систем управления экспериментальным методом и согласно формул, в случае задания системы с использованием передаточных функций. Закрепление полученных знаний на практике.
Необходимое время для выполнения работы: - 2 академических часа.
Необходимые приборы и оборудование:
Компьютер, совместимый с IBM PC, ОЗУ не менее 512 Мб.
Операционная система WINDOWS *.
Математический пакет MATLAB Version *.
Форма отчётности студентов: индивидуальный отчёт с типовым титульным листом и результатами моделирования.
Защита работы: собеседование с преподавателем по контрольным вопросам, выполнение индивидуальных заданий.
1 Теоретическая часть
1.1 Временные характеристики линейных систем управления
Временные характеристики вводят с целью изучения поведения САУ во временной области, когда о свойствах элемента (системы) можно судить на любом этапе управления по его реакции на поступающие воздействия [1, 4, 7, 8]:
единичный мгновенный импульс (дельта функция Дирака
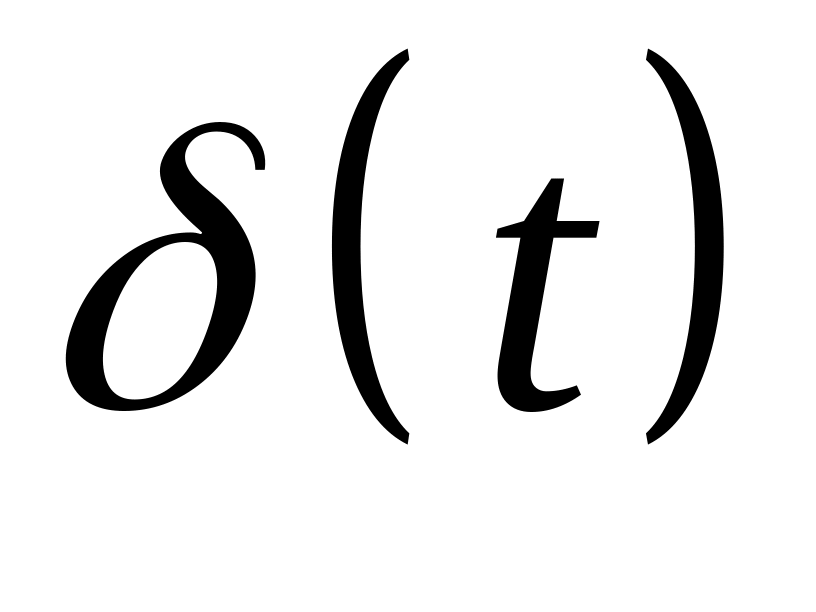).единичную ступенчатую функцию.
Единичное
ступенчатое воздействие
– это воздействие, которое мгновенно
возрастает от нуля до единицы и далее
остаётся постоянным.
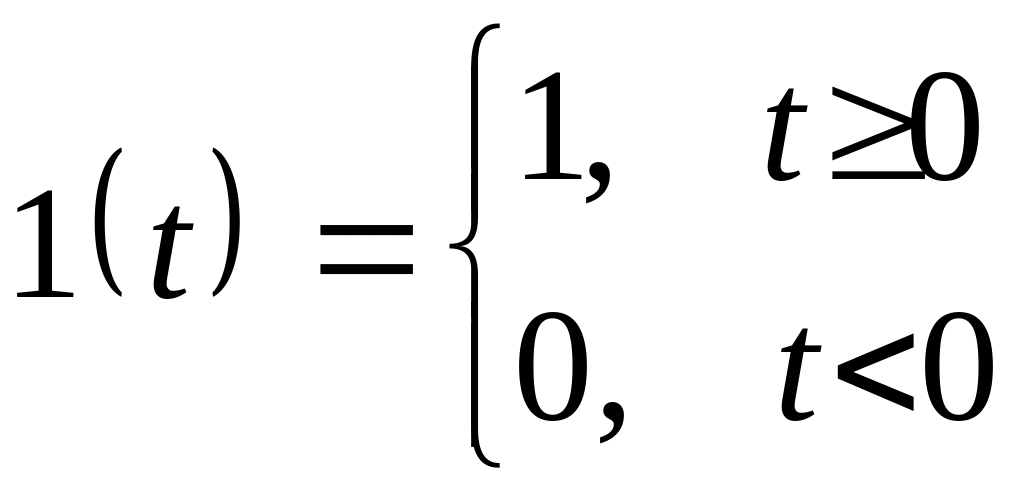
- это мгновенное изменение нагрузки на валу электрического двигателя, мгновенный поворот входного валика следящей системы.
Реакцию
системы на единичное ступенчатое
воздействие при нулевых начальных
условиях называют переходной
функцией, а
её графическое изображение переходной
характеристикой и обозначают
.
Единичный
мгновенный импульс
–
это математическая идеализация предельно
короткого импульсного сигнала с
бесконечно большой высотой (
)
и бесконечно малой ширинs
(0), но площадь которого равна 1.
.
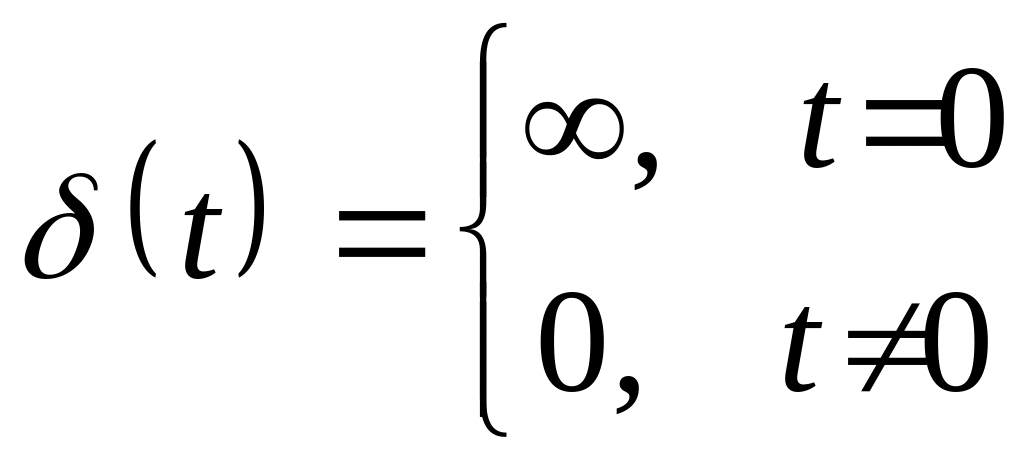Функция
связана с 1(t)
следующими соотношениями
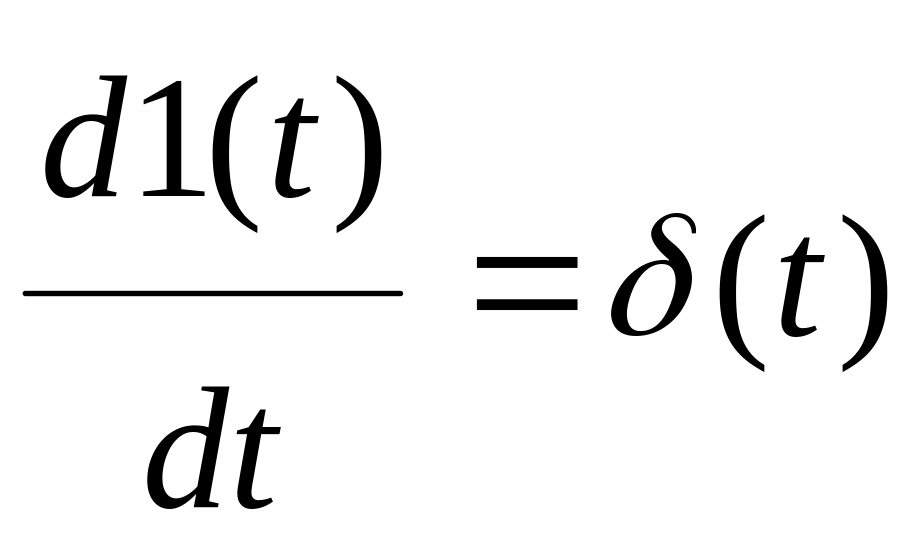или
.
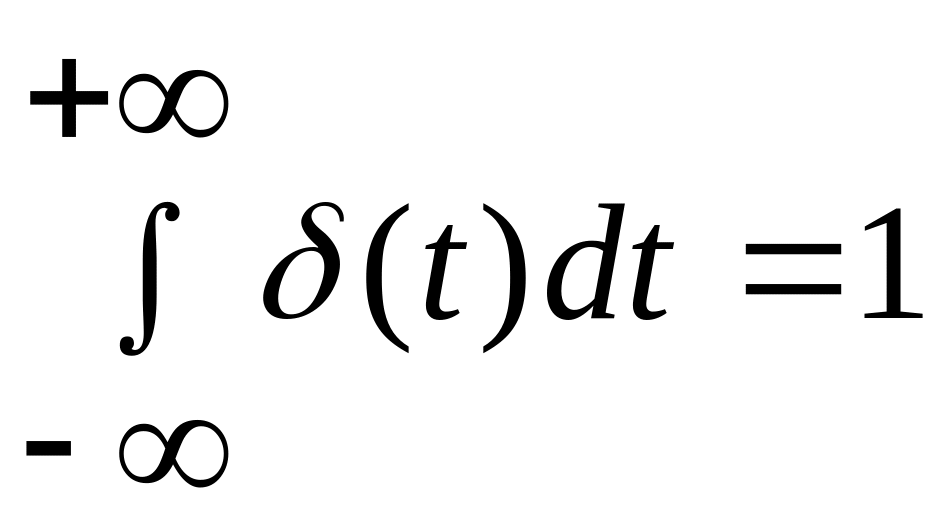– например, кратковременный удар нагрузки на валу двигателя, кратковременный ток короткого замыкания, отключаемый плавкий предохранитель.
Реакцию
системы на единичный мгновенный импульс
при нулевых начальных условиях называют
импульсной
переходной (весовой) функцией,
а её графическое изображение импульсной
(весовой) характеристикой и обозначают
.
Импульсная переходная функция (ИПФ) должна удовлетворять двум условиям:
,
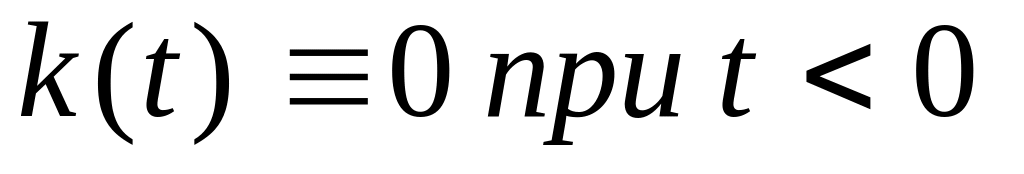т.е. переходный процесс не может
возникнуть раньше причины его вызвавшей
(условие физической реализуемости);
,
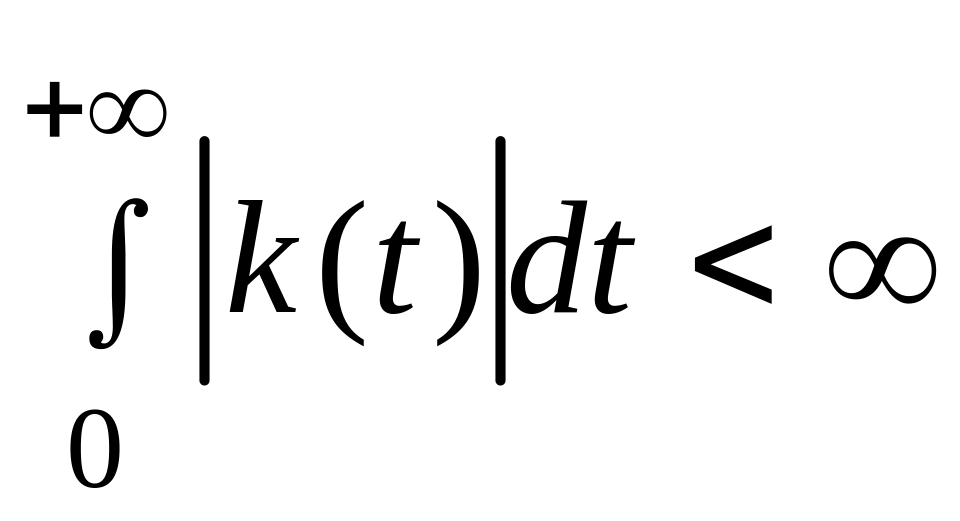т.е. переходный процесс должен быть
ограниченным.
Функция связана с существует определённая зависимость
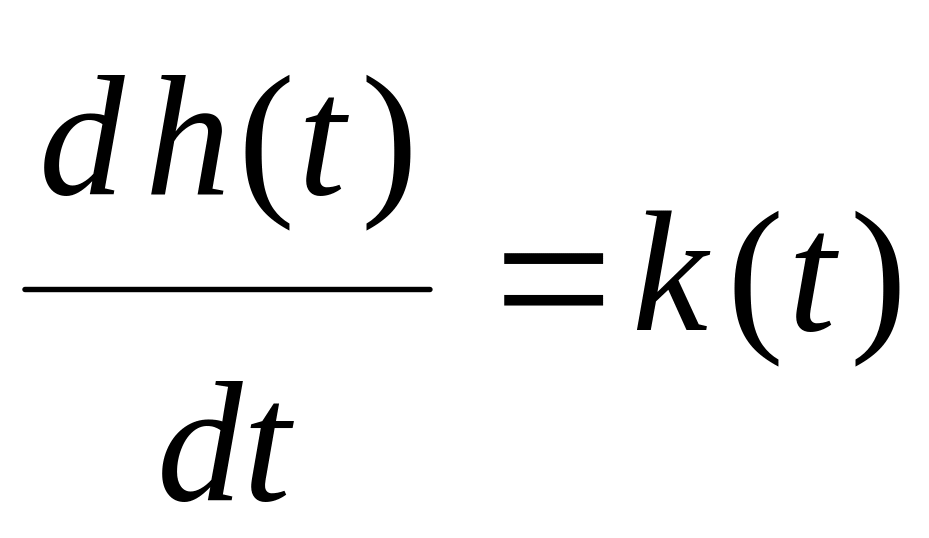или
