3 Построение области стойкости системы методом d-разбиения по одному параметру

На практике бывает необходимо знать не только запас, который можно оценить с помощью какого - либо критерия устойчивости, но и всю область устойчивости по параметрам. Этой цели служит метод D - разбиения, позволяющий построить такую область в плоскости одного или двух параметров. [3]

Пусть дано характеристическое уравнения системы, в которой исследуемый параметр D входит линейно в характеристическое уравнение системы.

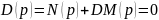
Заменим p на jw:

Выделим из этого уравнения параметр D:

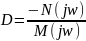
Изменяя частоту от минус бесконечности до плюс бесконечности, получим кривую D - разбиения. Кривая D разбивает плоскость параметра на несколько областей с различным условием устойчивости, для определения которого необходимо выбрать по одному значению D в каждой из них и проверить устойчивость с помощью какого-либо критерия. Если система устойчива при выбранном D, то она будет устойчива и при других значениях из этой области. [3]

На рисунке 3.1 показана кривая D разбиения, только замкнутая область D определяет пределы изменения данного параметра, при которых система является устойчивой, то есть это вторая область. [3]

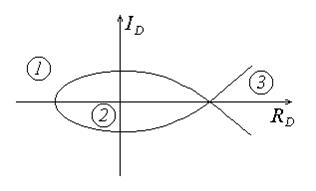
Рисунок 3.1 – Кривая D разбиения

3.1 Построение области d разбиения для исследуемой системы

Для построения области D-разбиения нужно из характеристического полинома системы выделить k и заменим s на jw. Изменяя частоту от минус бесконечности до плюс бесконечности, получим кривую D - разбиения. Определим зоны устойчивости и зоны неустойчивости и выберем коэффициент усиления k.

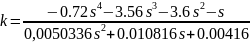
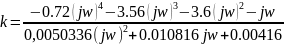
Из рисунка 3.2 видно две зоны – зона устойчивости и зона неустойчивости. То есть мы можем выбрать любой коэффициент усиления k из данной зоны. Выберем k=3000.

Рисунок 3.2 – D-разбиение по одному параметру

4 Оценка устойчивости замкнутой и разомкнутой системы

Построим модель системы в среде MatLab Simulink.

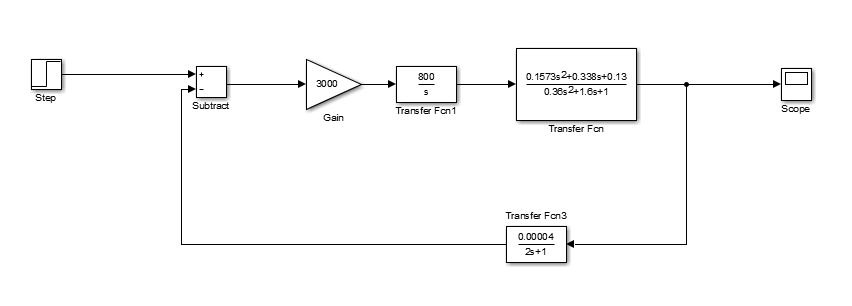
Рисунок 4.1 – Модель нескорректированной системы

Используя скрипт, приведенный ниже рассчитаем передаточные функции разомкнутой и замкнутой системы, а также характеристический полином системы.

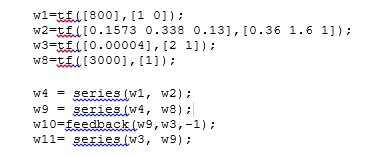
Рисунок 4.2 – Скрипт на языке MatLab для нахождения ПФ

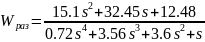
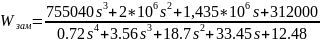
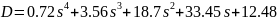
4.1 Оценка устойчивости разомкнутой системы по корням характеристического уравнения

Для того, чтобы линейная САУ была устойчивая, необходимо, что бы все корни характеристического уравнения были левыми, то есть имели отрицательную вещественную часть. Найдем корни характеристического уравнения. [4]

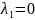
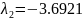
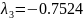
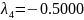
Так как все корни левые, то система является устойчивой. Однако система находится на границе устойчивости, так как есть корень, который равен нулю.

4.2 Оценка устойчивости замкнутой системы по критерию Гурвица

Для того, чтобы оценить устойчивость замкнутой системы по критерию Гурвица необходимо построить главный определитель Гурвица из коэффициентов ХУ.

Det=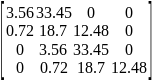

1) Первый определитель = 3.56;

2) Второй определитель = 42,488;

3) Третий определитель = 1263,057072;

4) Четвертый определитель = 15762.95225856;

По Гурвицу система устойчива, так как все определители Гурвица до 4 порядка больше нуля и 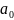больше нуля.

4.3 Оценка устойчивости замкнутой системы по критерию Михайлова

Для того, чтобы замкнутая система была устойчива по Михайлову необходимо, чтобы кривая Михайлова при изменении частоты от нуля до бесконечности, начиналась на действительной положительной полуоси и проходила n квадрантов против движения часовой стрелки, нигде не обращаясь в ноль, где n порядок характеристического полинома. [4]

Воспользуемся скриптом (рис. 4.3)

Рисунок 4.3 – Скрипт на языке MatLab для построения годографа Михайлова

Из рисунка 4.4 видно, что система устойчивая по Михайлову, так как годограф Михайлова начинается на действительной положительной полуоси, проходит 4 квадранта против хода часовой стрелки.

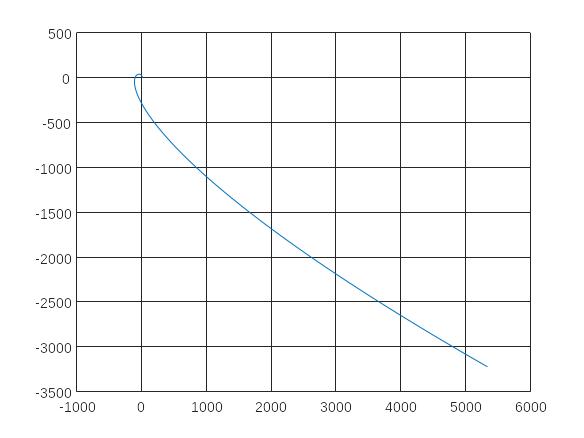
Рисунок 4.4 – Годограф Михайлова