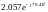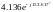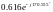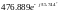ВоронинаРГР2

МИНИСТЕРСТВО НАУКИ И ВЫСШЕГО ОБРАЗОВАНИЯ РОССИЙСКОЙ ФЕДЕРАЦИИ

Федеральное государственное автономное образовательное учреждение высшего образования

«НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТОМСКИЙ ПОЛИТЕХНИЧЕСКИЙ УНИВЕРСИСТЕТ»

Инженерная школа энергетики

Отделение электроэнергетики и электротехники

Расчет постоянной цепи разветвленного тока

Расчетно-графическая работа №2

Вариант 104

Исполнитель:
студент группы	5А84		Воронина Е.А.
Руководитель:
к.т.н., доцент ОЭЭ ИШЭ			Шандарова Е.Б.

Томск 2020

Задание

Для данной схемы с постоянными во времени источниками ЭДС и тока, принимая

выполнить следующее:

1. Изобразить схему, соединяющих узлы, помеченные буквами, указав их номера и направления.

2. Определить токи во всех схемы и напряжение на зажимах источника

тока:

- по законам Кирхгофа;

- методом контурных токов;

3. Составить баланс полной, активной и реактивной мощностей.

4. Построить лучевую диаграмму токов и топографическую диаграмму напряжений.

5.Определить показания вольтметра.

6. Определить ток в ветви ab методом эквивалентного генератора.

7. Рассчитать мощность. Pab и построить зависимость Pab(R).

8. Сравнить результаты вычислений, оценить трудоёмкость методов расчёта и сформулировать выводы по выполненным пунктам задания.

Исходные данные

Для заданной схемы дано:

Исходные данные для расчёта представлены в таблице 1.

_{Таблица 1 – Исходные данные для расчёта}

E1	E2	J	α1	α2	β	R	L	C	w	M
В	В	А	град	град	град	Ом	мГн	мкФ	рад/с	мГн
110	200	5	0	-90	0	100	318.47	31.8	314	L/2

Схема для расчёта изображена на рис.1

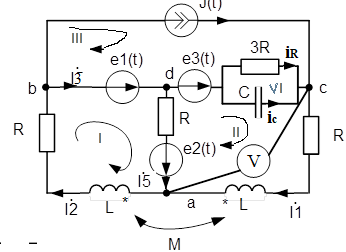
Рисунок 1 – Исходная схема

Так как e₃ (t)=0, то узлы a и m, k и c.Данная схема имеет:

- 4 узла (n_y);

- 7 ветвей (n_в);

- 5 неизвестных токов (n_I).

2. Определяются токи во всех ветвях схемы и напряжение на зажимах источника тока

2.1 Метод законов Кирхгофа

На рисунке 2 изображена схема для расчёта с выбранным направлением обхода контуров

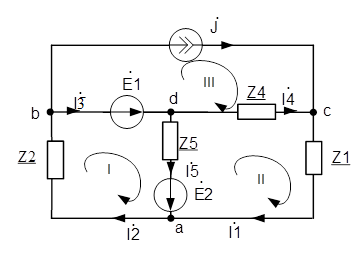
Рисунок 2 – Схема для расчёта методом законов Кирхгофа

Число уравнений, которые необходимо составить по:

- первому закону Кирхгофа рассчитывается по формуле

n₁ = n_y – 1 = 4 – 1 = 3;

- по второму закону Кирхгофа рассчитывается по формуле

n₂ = n_в – n₁ = 7 – 3 = 4.

Составляются уравнения по первому закону Кирхгофа:

- для узла d:

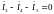
- для узла c:

- для узла b:

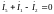
Для четырех контуров составляется уравнения по второму закону Кирхгофа:

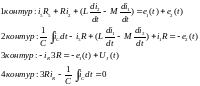
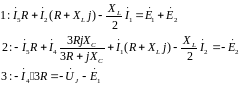
Перейдем от дифференциальных уравнений к символическому методу, преобразуем уравнения с синусоидальными напряжениями и токами в алгебраические уравнения с комплексными величинами:

Рассчитаем без учёта взаимной индуктивности М комплексные сопротивления ветвей, соединяющих узлы a, b, c, d.

Узел b:

Узел d:

Узел а:

Контур 1:

Контур 2:

Контур 3:

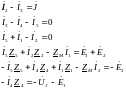
Метод законов Кирхгофа: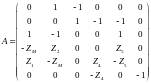

Решение матричного уравнения:

Значение токов и напряжения на источнике тока в алгебраической форме: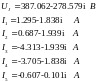

Переведем значения токов и напряжения в показательную форму:

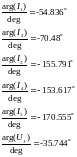
Значение токов и напряжений в показательной форме:

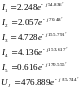
Результаты расчётов сведены в таблицу 2.

_{Таблица 2 – Результаты расчёта методом законов Кирхгофа}

I1, А	I2, А	I3, А	I4, А	I5, А	UJ, В

2.2 Метод контурных токов

Схема с выбранными контурными токами и их направлением изображена на рисунке 3.

Рисунок 3 – Схема для расчётов методом контурных токов

Рассчитывается число контурных токов, которые необходимо направить в схеме:

n_кт = n_в – n_у + 1 = 6 – 4 + 1 = 3.

Рассчитывается число контурных уравнений, которые необходимо будет решить:

n_ку = n_I – n_у + 1 = 5 – 4 + 1 = 2.

Контурные токи обозначаются как:

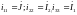
Для двух неизвестных контурных токов составляется уравнения:

- для контурного тока I₂₂:

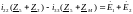
-для контурного тока I₃₃:

Метод контурных токов:

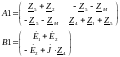
Решение матричного уравнения:

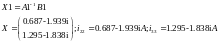
Далее находятся реальные токи в ветвях схемы, с учётом контурных токов, проходящих в этих ветвях, и напряжение на зажимах источника тока (по второму закону Кирхгофа для контура с I₃₃₎

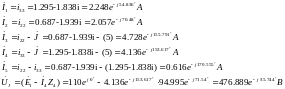
Результаты расчётов методом контурных токов сведены в таблицу 3.

Таблица 3 – Результаты расчёта методом контурных токов

I1, А	I2, А	I3, А	I4, А	I5, А	UJ, В

Записываем мгновенные значения тока в ветви ab и напряжения на зажимах источника тока:

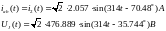
3. Рассчитываем балансы активной и реактивной мощностей:

3.1. Полная вырабатываемая мощность всех источников:

Для расчета полной мощности берем сопряженные токи токам I3 и I5

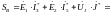
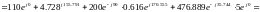
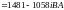
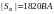
3.2 Активная потребляемая мощность:

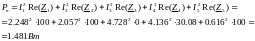
,где I₁,I₂ … - действующие значения (модули) токов.

3.3 Реактивная потребляемая мощность:

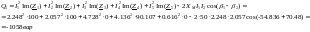
3.4 Погрешность расчетов

- По активной мощности:

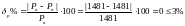
-По реактивной мощности:

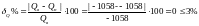
4.Строим лучевую векторную диаграмму токов Масштаб векторов тока m₁=10 A/cм и на комплексной плоскости строим векторы токов, которые выходят из начала координат каждый под своим углом (рис.4).

Рисунок 4 – Векторная диаграмма токов

Для упрощения построения топографической диаграммы напряжений на комплексной схеме расставляем стрелки напряжений навстречу направлениям токов. Использую закон Ома и учитывая наличие индуктивных связи, проводим расчет этих напряжений:

Рассчитываем комплексные потенциалы узлов схемы:

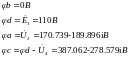
Принимаем масштаб векторов напряжения и потенциалов узлов м=0.5B(рис.5)

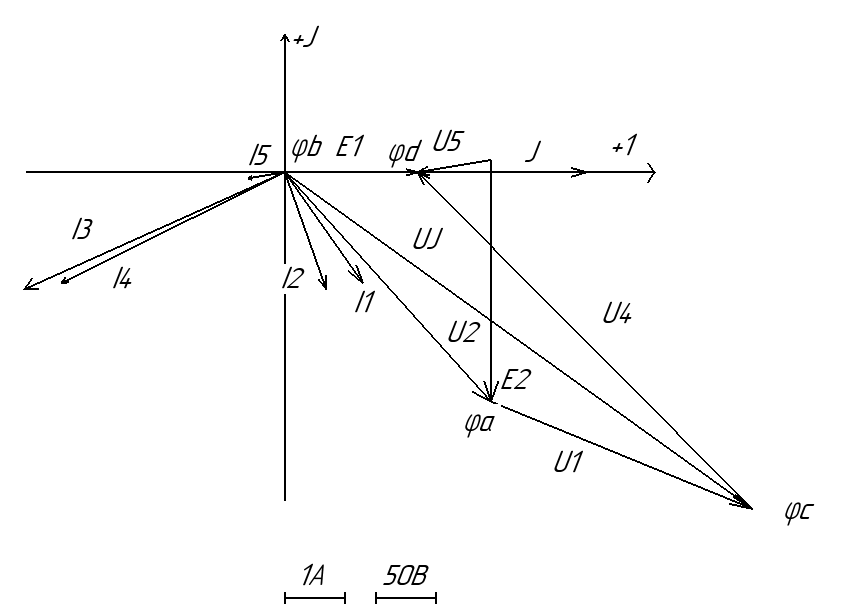
Рисунок 5 – Топографическая диаграмма напряжений и токов

5. Определение показаний вольтметра.

Определение показания вольтметра аналитически, как разность потенциалов между точками включения вольтметра, т. е. между узлами а и с:

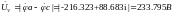
Определение показания вольтметра графически:

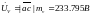
6. Метод эквивалентного генератора

Схема для расчёта тока I₂ методом эквивалентного генератора изображена на рисунке 4.

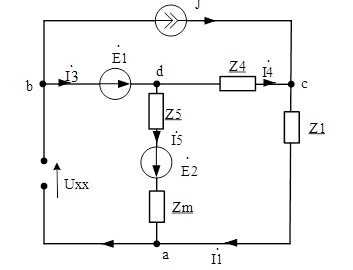
Рисунок 6 – Схема для расчёта методом эквивалентного генератора

Напряжение холостого хода U_XX в ветви ab находится по второму закону Кирхгофа.

Сопротивление эквивалентного генератора R_Г. Схема для расчёта эквивалентного сопротивления генератора изображена на рисунке 5.

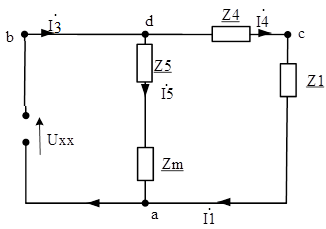
_{Рисунок 7 – Схема для расчёта эквивалентного сопротивления}

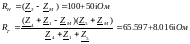
Находится ток короткого замыкания I₂^(кз) эквивалентного генератора:

Находится ток в ветви ab аналитически по двум формулам:

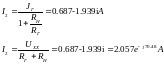
Изменяя величину сопротивления R ветви ab от 0 до 10Rg=33.043 Ом рассчитываем мощность Pab, которая выделается в виде тепла в этом сопротивлении:

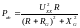
Результаты расчетов мощности представлены в таблице: ….

R,Oм	0	66	132.2	198.3	264.3	330.5	396.512	462.597	528.683	660.853
Pab	0	496.6	441	371.7	316.9	274.9	242.304	216.349	195.302	163.346

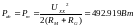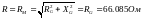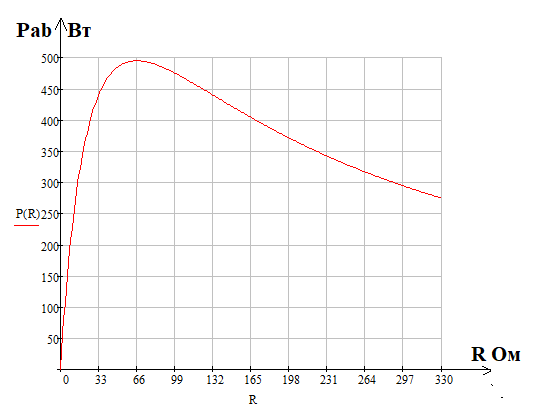
Максимум мощности наблюдается при . Строим график зависимости P_ab=f(R).

Вывод

Токи в схемах были рассчитаны методами: законов Кирхгофа и- контурных токов.

При расчёте токов всеми этими методами значения токов в ветвях по-лучились одинаковыми.

Составлен баланс мощностей.

Погрешность расчетов по активной мощности равна 0. Погрешность расчетов по реактивной мощности равна 0.204%, что меньше 3%.

Построены лучевая диаграмма токов и топографическая диаграмма напряжений, определено показание вольтметра теоретически и графически.

Также был рассчитан ток ветви аb методом эквивалентного генератора.

Рассчитана мощность Pab и построить зависимость Pab(R).