Лабораторные / ЛР2 Выбор решения в условиях неопределённости

ФГБОУ ВО

Уфимский государственный авиационный технический университет

Кафедра УИ

Отчёт

по лабораторной работе №2

по дисциплине «Организация и планирование производства»

Тема: «Выбор решения в условиях неопределённости. Стратегические игры»

Выполнил: ст. гр. И-208

Исламова Р. Р.

Принял: к. э. н., доц.

Кузнецова Н. П.

Уфа 2021 г.

Цель работы: изучение методов принятия решения при неопределённости в поведении противника.

Задача

Идёт борьба между двумя фирмами А и В за рынок спроса транзисторных приёмников. У каждой из сторон имеется своё множество стратегий:

Игрок А	Игрок В
А1: Снизить цену единицы продукции;	В1: Снизить цену единицы продукции;
А2: Создать модификацию товара с уменьшенным весом;	В2: Создать модификацию товара с уменьшенным весом;
А3: Создать модификацию с дополнительным диапазоном частот.	В3: Создать модификацию с дополнительным диапазоном частот.
	В4: Модификация источника электроэнергии (с подзарядкой от сети).

Используя данные платёжной матрицы, определить оптимальную смешанную стратегию игрока А и игрока В.

Решение

Платёжную матрицу изобразим в таблице 1.

Таблица 1 – Платёжная матрица

А В	В1	В2	В3	В4	α
А1	3	4	6	1	1
А2	2	8	4	3	2
А3	10	3	1	7	1
β	10	8	6	7

1. Платежная матрица

2. Перевод в исходную и двойственную задачи ЛП

3. Значение среднего выигрыша

4. Опт. Стратегии

В строку β записываем наибольшие значения каждого столбца, в столбец α – наименьшие значения каждой строки. Матрица игры не имеет седловую точку, следовательно, сразу определить оптимальную стратегию нельзя.

Игроки должны применить смешанные стратегии р_a и q_a.

Воспользуемся методами линейного программирования. Для этого сведём матричную игру к задаче линейного программирования.

Примем вероятности стратегии игрока А равными

p₁ = 0,26,

p₂ = 0,36,

p₃ = 0,38,

а игрока В равными

q₁ = 0,26,

q₂ = 0,30,

q₃ = 0,35,

q₄ = 0,09.

γ – цена игры, удовлетворяющая условиям

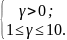
Пусть игрок 2 применяет свою чистую стратегию В₁, а игрок 1 – свою оптимальную стратегию р. Тогда средний выигрыш игрока 1 будет равен

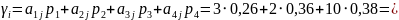5,3, что удовлетворяет условию.

Введём обозначения:

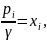
тогда

x₁ = 0,05,

x₂ = 0,07,

x₃ = 0,05.

Получаем линейную функцию:

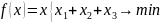
Из решения задачи линейного программирования находим цену игры игрока А:

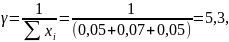
что соответствует условию.

Введём обозначения:

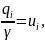
тогда

u₁ = 0,06,

u₂ = 0,07,

u₃ = 0,08.

u₄ = 0,02.

Из решения задачи линейного программирования находим цену игры игрока В:

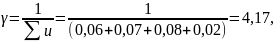
что соответствует условию.

Решая исходную задачу, получаем результаты, представленные на рисунке 1.

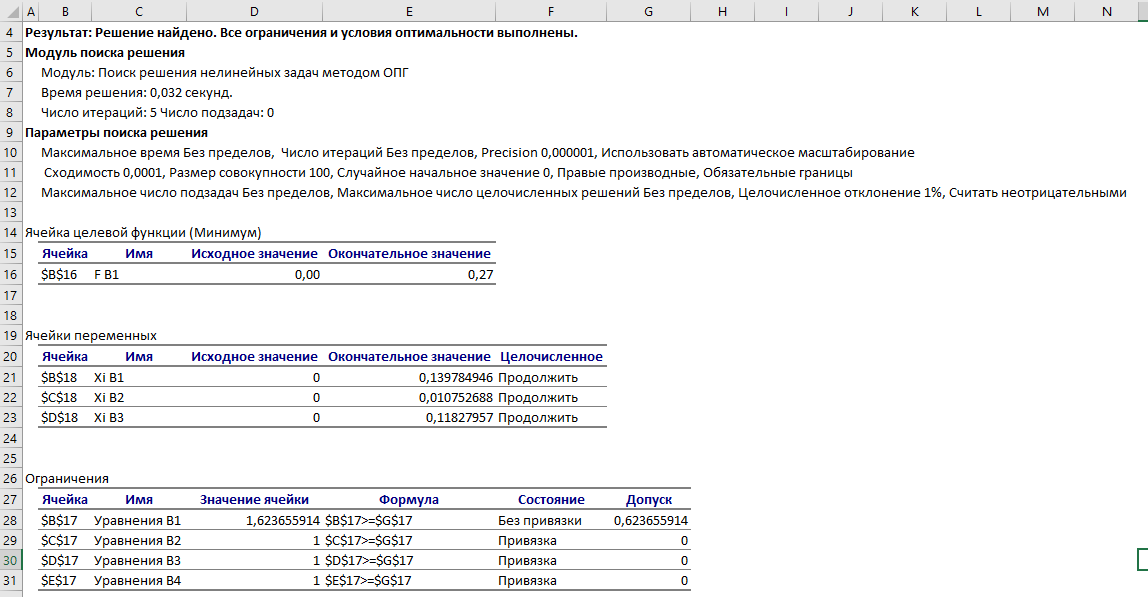
Рисунок 1 – Результаты решения исходной задачи

Решим двойственную задач. Получаем результаты, представленные на рисунке 2.

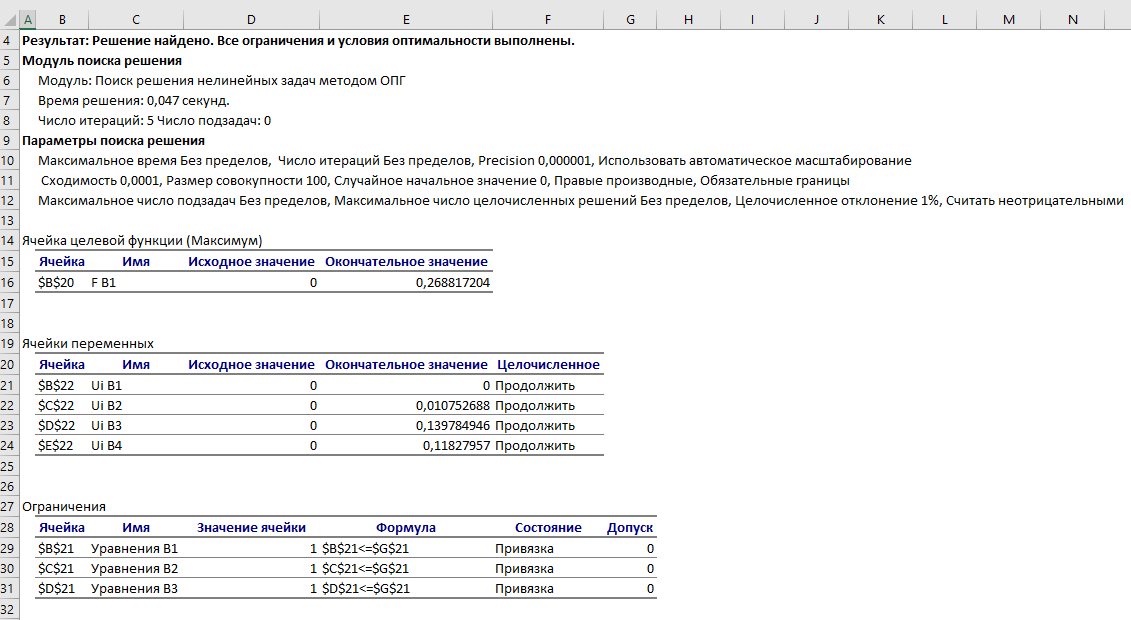
Рисунок 2 – Результаты решения двойственной задачи

Цена игры составляет γ = 5,3.

Средний выигрыш каждого игрока составляет 3,72.

Оптимальные стратегии для каждого игрока представлены на рисунке 3.

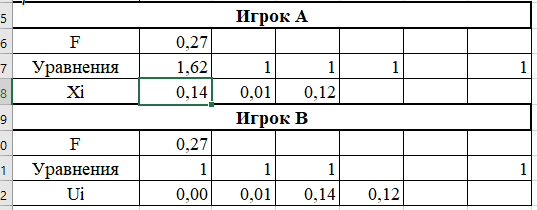
Рисунок 3 – Оптимальные стратегии каждого игрока

Вывод: в ходе лабораторной работы был изучен метод принятия решения при неопределённости в поведении противника.

Ответы на контрольные вопросы:

1. Какие игры называются играми с седловой точкой?

Играми с седловой точкой называются такие игры, для которых нижняя цена равна верхней, то есть .

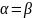2. Что называют чистой ценой игры?

Чистой ценой игры называют общее значение нижней и верхней цены игры в играх с седловой точкой.

3. Чем отличаются смешанные стратегии игроков от чистых стратегий?

Смешанные стратегии являются сложными стратегии, так как в них случайно применяются две и более чистых стратегии с определенными частотами.

4. Как определяется оптимальная смешанная стратегия игроков?

Оптимальная смешанная стратегия игроков определяется следующим образом: