
Отчёт по лабораторной работе №3 по дисциплине «Программная инженерия управляющих систем»
|
выполнили студенты группы ПИН – 41 Бордюжа Якупова Москвитина Доникян Карасева Печенова Тиховский Рыжов Семенов Гончаров Камбулов Козлов Илларионов
Задания Задание 1
Решение
Стандартный генератор случайных чисел выдает квазинезависимую последовательность чисел, равномерно распределенную в диапазоне от [0, 1]. Для U[0,1]:
Так как,
по условию, математическое ожидание
у
Перейдем теперь к распределению U[-0,5 , 0,5]:
По условию,
Форма распределения такого сигнала остается равномерной, а отсчеты по-прежнему квазинезависимые. В итоге,
последовательность данных операций
привела нас от равномерного распределения
U[0,1] к равномерному распределению
Гистограмма для сигнала соответствует равномерному распределению. Границы
изменений флуктуаций для сигнала
это
параметры
Задание 2
Решение Сигнал
Согласно центральной предельной теореме сигнал стремится к нормальному распределению.
Здесь мы воспользовались теоремой сложения математических ожиданий, которая гласит, что математическое ожидание суммы случайных величин равно сумме их математических ожиданий.
На основе свойства
дисперсии : = 1/9 D[
На основе того, что случайные величины независимы, дисперсия суммы случайных величин равна сумме их дисперсий . Т.к. стремится к нормальному распределению, можно воспользоваться правилом трёх сигм, которое гласит, что случайная величина отклонится от своего математического ожидания больше чем на три среднеквадратических отклонения, практически равна нулю. Из этого правила и вытекают границы флуктуации [-3;+3]. Гистограмма напоминает нормальный закон распределения. |
Задание 3
Решение “Гауссовость” сигнала
вытекает из центральной предельной
теоремы, которая гласит, что сумма n
независимых одинаково распределённых
случайных величин имеет распределение
близкое к
«Белый шум» сигнала можно объяснить тем, что независимые равномерно распределенные случайные значения сигнала по ЦПТ перешли в независимые нормально распределенные случайные значения. То есть «белошумность» это следствие изначальной независимости случайных величин. |
Задание 4

Решение
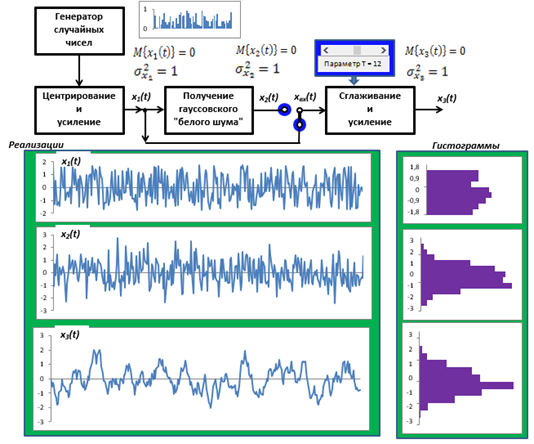
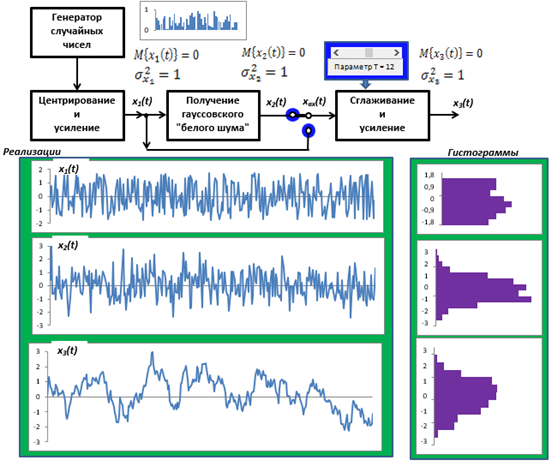
Сигнал получен с помощью рекуррентного соотношения:
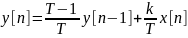
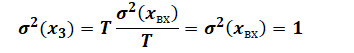
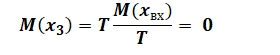
Дисперсия функции на выходе динамического
объекта практически всегда меньше дисперсии флуктуаций на входе,
причем сглаживание тем больше, чем более инерционен объект
по сравнению с временными флуктуационными характеристиками
ковариационного сигнала на входе.
Отметим, что динамические звенья оказывают
явное сглаживающее воздействие на входные сигналы, делая их
более плавными и снижая уровень их флуктуаций (на уровне кова-
риационных функций явно прослеживается уменьшение координат
при нуле, т.е. уменьшение дисперсии).
Окрашенный шум полученный из Гауссового шума обладает теми же статистическими параметрами, что и шум полученный из равномерного. Но он более разреженный.


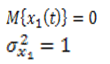
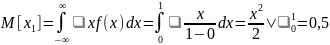
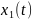 равно
0, то нужно вычесть из каждого случайного
числа 0,5.
равно
0, то нужно вычесть из каждого случайного
числа 0,5.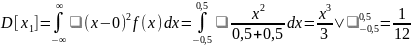
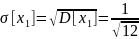
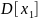 =1.
Значит, для получения необходимой
дисперсии следует умножить каждый
элемент на
=1.
Значит, для получения необходимой
дисперсии следует умножить каждый
элемент на
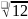 .
.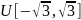 .
.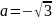 и
и
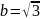 равномерного распределения.
равномерного распределения.
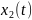 получен
с помощью расчетного соотношения
получен
с помощью расчетного соотношения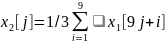
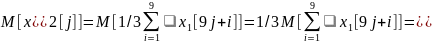
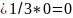
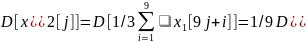 ]
=
]
=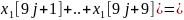
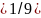
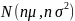 .
.