2.6. Потенціальна енергія

2.6.1. Градієнт скалярної функції. Якщо у кожній точці простору задано число φ = φ(x,y,z), то говорять, що задано скалярне поле. Прикладом скалярного поля може бути поле значень температур у кожній точці в об’ємі газу, або значення електричного потенціалу поблизу зарядженого тіла.

Нехай у просторі задано скалярне поле φ = φ(x,y,z) і векторне поле .

Якщо мають місце такі співвідношення:

,

то векторне поле називається градієнтом скалярної функції φ(x,y,z). Величина є частковою похідною функції φ. Часткова похідна – це похідна за однією змінною (у даному випадку, за змінною x) від функції багатьох змінних. Наприклад, від функції Ф(x) = 5cos(xy) +3 x²z – 48y часткова похідна за змінною x дорівнює

.

Позначається градієнт таки чином:

,

– диференціальний оператор “набла”:

.

2.6.2. Приклад на обчислення градієнта

Знайти градієнт від скалярної функції φ(x,y,z) = x²+y²+z².

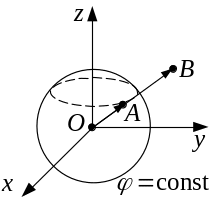
Рис. 2.6

Розв’язок. Спочатку знайдемо часткові похідні

.

Позначимо вектором градієнт даної функції:

.

На рис. 2.6 радіус-вектор , точка А лежить на поверхні сфери, рівняння якої

φ(x,y,z) =const;

градієнтом функції φ(x,y,z) є подвійний радіус-вектор .

2.6.3. Потенціальне поле

Якщо існує градієнт функції , то векторне поле називається потенціальним. Функція φ називається потенціальною функцією.

Теорема

Якщо векторне поле потенціальне, то воно консервативне.

Доведення:

Потрібно довести той факт, якщо векторну функцію можна представити у вигляді градієнта скалярної функції , то робота по замкненому контуру дорівнює нулю: .

Підставимо у формулу для визначення роботи вирази для градієнта та вектора елементарного переміщення й отримаємо:

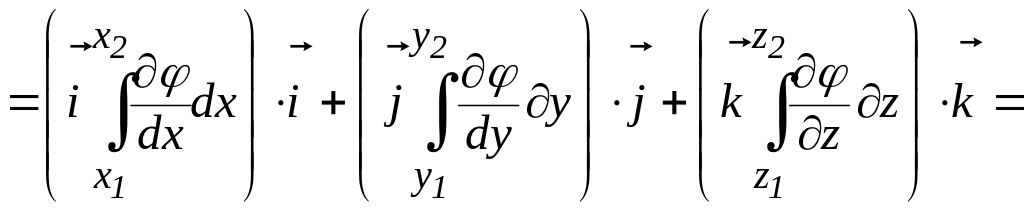
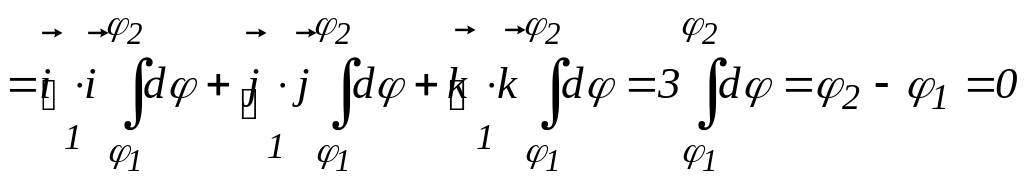, (2.14)

оскільки інтегрування ведеться по замкненому контуру, тому ₁ = ₂ , а деякі члени у другому рядку не враховані, тому що в них містяться скалярні добутки різних ортів, які дорівнюють нулю ( ). Теорему доведено.

Завдання. Самостійно довести зворотне твердження: якщо поле консервативне, то воно потенціальне.

2.6.4. Потенціальна енергія – це потенціальна функція з протилежним знаком:

U(x,y,z) = – (x,y,z). (2.15)

Як випливає з формули (2.14), робота консервативного поля сил дорівнює зміні потенціальної функції:

А_конс = ₂ – ₁ . (2.16)

Врахувавши визначення потенціальної енергії (2.15), виразимо роботу консервативних сил через потенціальну енергію:

А_конс = U₁ – U₂ . (2.16)

Сила виражається через потенціальну функцію як

,

а через потенціальну енергію –

.

2.6.5. Приклади потенціальних енергій

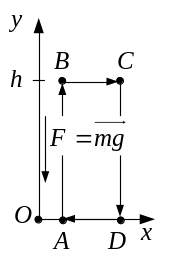
Рис. 2.7

1) Поле сил тяжіння Землі. Потенціальна енергія є функцією лише однієї змінної – висоти над поверхнею Землі:

U = mgh.

Переконаємося у тому, що це консервативне поле. Для цього обчислимо роботу вздовж замкненого контуру ABCDА (див. рис. 2.7).

Робота на відрізку АВ – –mgh; BC та DА – A = 0; на CD – mgh. Отже, робота вздовж замкненого контуру ABCDА дорівнює нулю:

.

2) Потенціальна енергія пружно стиснутої пружини:

.

Величини k і x визначені у пункті 2.3.4.

Одиниця вимірювання потенціальної енергії – джоуль (Дж).

2.6.6. Потенціальна енергія механічної системи (системи матеріальних точок) – це частина механічної енергії системи, яка залежить лише від взаємного розташування частинок системи та їхнього положення зовнішньому силовому полі.

Якщо будь-які дві частинки всередині системи взаємодіють між собою із силами, модулі яких залежать лише від відстані між ними, то всі сили всередині системи будуть консервативними і потенціальна енергія механічної системи складається з двох частин: U_вз – потенціальної енергії взаємодії між частинками системи (внутрішня потенціальна енергія) і U_зов – потенціальної у зовнішньому консервативному силовому полі.