
ЛР-4 Федорова Т-910
.pdf
Лабораторная работа «Потери напора по длине трубопровода» |
Стр. 2 |
Лабораторная работа
ПОТЕРИ НАПОРА ПО ДЛИНЕ ТРУБОПРОВОДА
Цели работы:
1)Определение потерь напора по длине трубопровода опытным путём.
2)Определение коэффициента гидравлического трения опытным путём.
3)Определение области гидравлического сопротивления.
4)Определение коэффициента гидравлического трения по эмпирическим формулам для соответствующей области гидравлического сопротивления.
Основные теоретические сведения.
Поток жидкости в трубопроводе затрачивает энергию на преодоление сил трения, которые возникают как в самой жидкости, так и между жидкостью и стенками трубопровода. Силы трения, преодолеваемые потоком, называются г и д р а в л и ч е с к и м и с о п р о т и в л е н и я м и . Поскольку удельная энергия жидкости, отнесенная к единице веса, именуется в гидравлике напором, затраты энергии на преодоление сил трения получили название потерь напора.
Различают два вида гидравлических сопротивлений и обусловленных ими потерь напора:
1) П о т е р и н а п о р а п о д л и н е – представляют собой затраты энергии на преодоление гидравлических сопротивлений, равномерно распределенных по длине
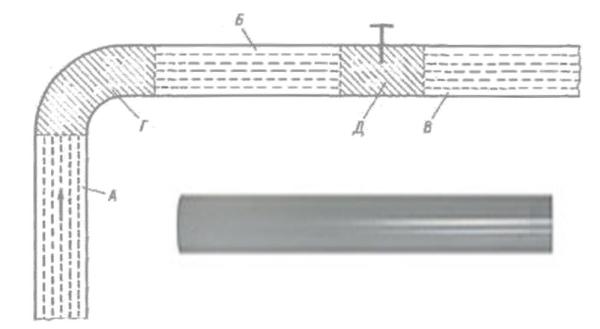
потока. Потери напора по длине потока возникают в случае равномерного движения жидкости. На рисунке потери напора по длине обозначены А, Б, В.
Гидравлические сопротивления по длине в напорных трубопроводах характеризуются безразмерным коэффициентом гидравлического трения λ, который входит в формулу Вейсбаха-Дарси для вычисления потерь напора по длине.
2) М е с т н ы е п о т е р и н а п о р а м – представляют собой затраты энергии на преодоление гидравлических сопротивлений, которые обусловлены локальными сопротивлениями, сосредоточенными на небольшом участке потока, например, на резком повороте, при резком расширении или резком сужении трубопровода и т. п. В отличие от потерь напора по длине потока, местные потери напора возникают при неравномерном движении жидкости. На рисунке местные потери напора обозначены Г и Д.
Лабораторная работа «Потери напора по длине трубопровода» |
Стр. 3 |
Н а п о р н о е д в и ж е н и е ж и д к о с т и – движение жидкости, при |
котором |
жидкость со всех сторон ограничена жёсткими стенками, нет свободной поверхности. Напорное движение возникает в условиях, когда труба полностью заполнена жидкостью, и гидродинамическое давление во всех точках живого сечения выше атмосферного.
Полная потеря напора в трубопроводе определяется суммированием потерь напора
по длине трубопровода на отдельных участках и местных сопротивлений: |
|
hw hl hм |
(1) |
где hl - потери по длине потока, м; hм - местные потери напора, м
Потери напора по длине трубопровода можно найти как опытным путём, так и по эмпирической формуле Вейсбаха-Дарси.
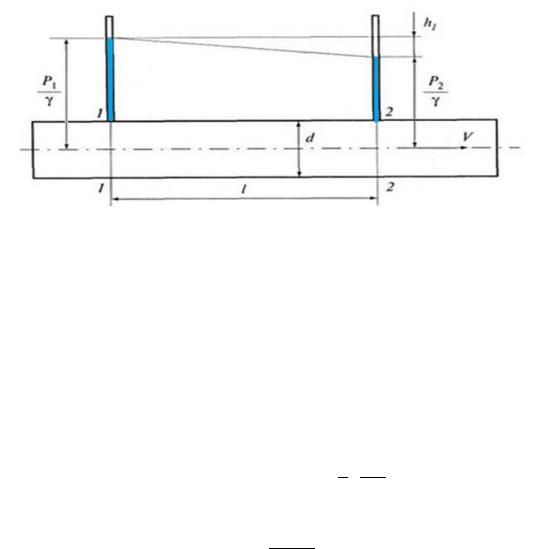
В прямом напорном трубопроводе потери напора по длине опытным путём можно определить как разность пьезометрических высот в начале и в конце рассматриваемого участка:
= |
1 |
− |
2 |
(2) |
|
|
|
||||
|
|
|
Для теоретического определения потерь напора по длине трубопровода также используют формулу Вейсбаха-Дарси:
= ∙ |
|
∙ |
2 |
|
|
|
(3) |
||
|
|
|||
|
|
2 |
||
где λ – коэффициент гидравлического трения, безразмерный; l–длина рассматриваемого участка трубопровода, м; d – внутренний диаметр трубы, м; V – средняя скорость движения потока воды на участке, м/с; g – ускорение свободного падения, м/с2
Падение давления на данном участке будет равно:
∆ = ∙ ∙ = ∙ ∙ 2 2, Па
Коэффициент гидравлического трения λ можно найти двумя способами: 1)опытным путём из формулы Вейсбаха-Дарси
= |
2 ∙ ∙ |
(4) |
∙2 |
2)в инженерной практике коэффициент гидравлического трения чаще всего вычисляют по эмпирическим формулам в зависимости от области гидравлического сопротивления.
Потери напора по длине трубопровода зависят от режима движения жидкости - для различных режимов используются разные формулы определения λ.
Режим движения потока жидкости определяют по числу Рейнольдса для напорных круглоцилиндрических труб (см. лабораторную работу «Режимы движения жидкости»):
= |
∙ |
(5) |
|
|
|||
|
|
где d – внутренний диаметр трубы; V – средняя скорость движения потока воды на участке; – кинематический коэффициент вязкости.

Лабораторная работа «Потери напора по длине трубопровода» Стр. 4
При Re<Reкр режим движения жидкости – ламинарный, область гидравлического сопротивления также называют о б л а с т ь л а м и н а р н о г о р е ж и м а .
Коэффициент гидравлического трения λ вычисляют по формуле, которая выведена теоретическим путем:
= |
64 |
(6) |
|
|
|||
|
|
При ламинарном режиме λ = f (Re) - коэффициент гидравлического трения λ зависит только от числа Рейнольдса, т. е. определяется скоростью движения жидкости, внутренним диаметром трубопровода и вязкостью жидкости. Принципиально важно то, что λ не зависит от шероховатости стенок трубы. Потери напора по длине прямо пропорциональны средней скорости движения жидкости. Установлено, что при ламинарном режиме движения потери напора минимально возможные.
В случае турбулентного режима не удается обойтись одной формулой для вычисления λ. Приходится различать гидравлически гладкие и шероховатые трубы. Различие между ними состоит в следующем. Силы молекулярного притяжения материала стенок трубы лишают возможности перемешивания частицы жидкости, которые находятся в непосредственной близости от стенок. Этот слой называют пограничным вязким (ламинарным) слоем. На самом деле считать движение в этом слое ламинарным не следует, поскольку в этом слое наблюдаются значительные продольные пульсации скорости. Однако практически отсутствуют пульсации поперек потока. Толщина пограничного слоя δ составляет сотые или тысячные доли внутреннего диаметра трубы.
Для вычисления толщины ламинарного пограничного слоя δ, мм, получена полуэмпирическая формула:
= |
30 |
(7) |
||
|
|
|||
√ |
||||
|
|
|||
где d – внутренний диаметр трубы, мм; λ – коэффициент гидравлического трения, безразмерный; Re – число Рейнольдса, безразмерный
Как видно из формулы (7), с увеличением скорости движения потока жидкости, а, следовательно, и с увеличением числа Рейнольдса – толщина пограничного ламинарного слоя δ уменьшается.
Внутренняя поверхность трубы не может быть абсолютно гладкой и обладает некоторой шероховатостью .
Ш е р о х о в а т о с т ь - характеризуется средней высотой неровностей внутри трубы. Шероховатость зависит от материала и технологии изготовления труб. Значение шероховатости обязательно указывается в паспорте на трубу.
В расчетах используются также величины относительной шероховатости ∆ и
относительной гладкости ∆.
Среднюю высоту неровностей стенок труб трудно измерить. Поэтому в гидравлических расчетах используется понятие эквивалентной шероховатости.
Э к в и в а л е н т н а я ш е р о х о в а т о с т ь э - это некоторая близкая к средней величине высота выступов на внутренней поверхности трубы, которая создаёт такие же потери напора по длине трубы, что и шероховатость, при расходе, равном действительному.
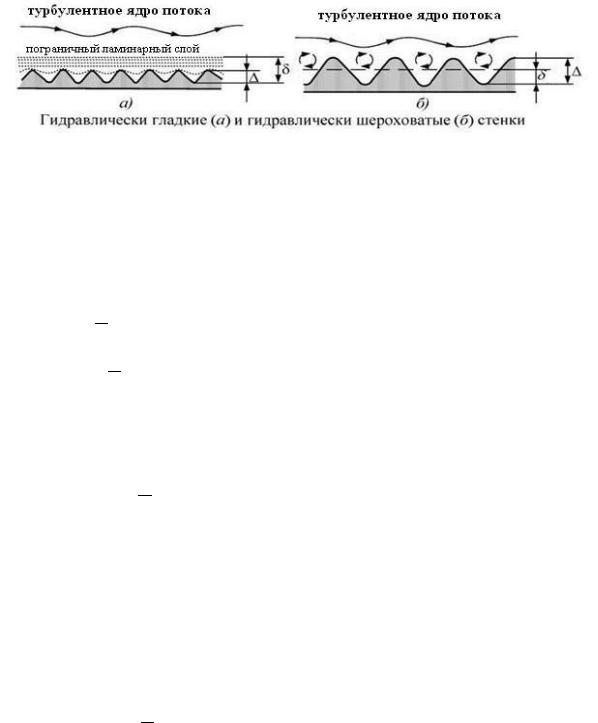
Если толщина вязкого пограничного ламинарного слоя 1 > ∆ (рис. 1а), то турбулентное ядро потока в процессе движения не соприкасается с неровностями стенок трубы. В этом случае коэффициент гидравлического трения не зависит от шероховатости, а стенки труб и сами трубы называются г и д р а в л и ч е с к и г л а д к и м и .
Лабораторная работа «Потери напора по длине трубопровода» |
Стр. 5 |
Если 2 < ∆ (рис. 1б), то турбулентное ядро потока соприкасается с неровностями |
|
стенок, λ зависит от шероховатости, а трубы называются |
г и д р а в л и ч е с к и |
ш е р о х о в а т ы м и .
Рис.1. Гидравлически гладкие и гидравлически шероховатые трубы
Как известно, толщина ламинарного слоя зависит от числа Рейнольдса и уменьшается с его увеличением. Поэтому отнесение труб к разряду гидравлических гладких или шероховатых производится с помощью числа Рейнольдса.
Зависимость толщины ламинарного слоя от числа Рейнольдса Re свидетельствует о том, что разделение труб на гладкие и шероховатые является условным. Труба, которая
при небольшой скорости движения жидкости ( < 10 |
|
) |
является |
|
|||
|
э |
|
|
гидравлическигладкой, может при увеличении скорости перейти в разряд шероховатых
труб ( > 10 ) и наоборот.
э
Гидравлически гладкими трубы являются при числах Рейнольдса в пределах
4000 < < 10 , область гидравлического сопротивления также называют о б л а с т ь
э
г и д р а в л и ч е с к и г л а д к и х т р у б .
При гидравлически гладких трубах λ = f (Re) коэффициент гидравлического трения λ зависит только от числа Рейнольдса и не зависит от скорости потока и параметров самой трубы (диаметр, шероховатость). Потери напора по длине в гидравлически гладких трубах пропорциональны средней скорости движения жидкости в степени 1,75.
Если > 10 , то труба относится к разряду гидравлически шероховатых труб
э
(см. табл.1). В гидравлически шероховатых трубах зависимость потерь напора по длине трубопровода hl от скорости потока V меняется с изменением числа Рейнольдса.
Поэтому выделены области доквадратичного сопротивления шероховатых труб и квадратичного сопротивления шероховатых труб.
При |
10 |
|
< < 500 |
|
имеем |
о б л а с т ь |
д о к в а д р а т и ч н о г о |
||
∆ |
∆ |
э |
|||||||
|
|
|
|
|
|
||||
|
|
э |
|
|
|
|
|
||
с о п р о т и в л е н и я , в которой hl прямо пропорциональна скорости в степени от 1,75 до 2,00 (т.е. до квадрата скорости). В этой области λ = f (Re, э/d) - коэффициент гидравлического трения λ зависит как от относительной шероховатости стенок труб э/d, так и от числа Рейнольдса Re.
При > 500 имеем о б л а с т ь к в а д р а т и ч н о г о с о п р о т и в л е н и я , в
∆э
которой hl прямо пропорциональна квадрату скорости. В этой области наблюдается зависимость λ = f (Δэ/d) - коэффициент гидравлического трения λ зависит только от
характеристик самой трубы – внутреннего диаметра d и шероховатости трубы э, и не зависит от числа Рейнольдса Re, а, следовательно, и от скорости потока V.
Формулы для расчета коэффициента гидравлического трения при турбулентном режиме не удается получить теоретическим путем. Предложены десятки эмпирических формул. В табл. 1 приведены те из них, которые относятся к числу наиболее часто применяемых в практических расчетах.

Лабораторная работа «Потери напора по длине трубопровода» Стр. 6
Таблица 1. Методика расчёта коэффициента гидравлического трения λ в напорных трубопроводах.
Режим движения жидкости
|
|
|
|
|
Турбулентный |
|
|
|
|
||||
|
|
|
|
|
|
Гидравлически шероховатые трубы |
|||||||
Ламинарный |
Гидравлически |
|
|
|
Область |
|
|
Область |
|||||
|
гладкие трубы |
доквадратичного |
квадратичного |
||||||||||
|
|
|
|
|
сопротивления |
|
сопротивления |
||||||
Re < 2300 |
4000 Re 10 |
d |
10 |
d |
Re 500 |
d |
500 |
d |
Re |
||||
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||
|
|
Э |
|
Э |
|
Э |
|
Э |
|
||||
|
|
|
|
|
|
|
|
|
|
||||
|
Формула Блазиуса |
Формула Альтшуля |
Формула Шифринсона |
||||||||||
64 Re
|
0,3164 |
||
Re |
0,25 |
||
|
|||
|
|
||
|
68 |
|
|
|
|
0.25 |
|
Э |
|
||||
0,11 |
|
|
|
|
||
|
|
|
|
|
|
|
Re |
|
d |
|
|
||
|
|
|
0.25 |
|
Э |
|
|||
0,11 |
|
|
|
|
|
|
|
|
|
|
d |
|
|
|
= ( ) |
= ( ) |
= ( , |
∆э |
= ( |
∆э |
hl ~ V1 |
hl ~ V1,75 |
⁄ ) |
⁄ ) |
||
hl ~ V1,75…2,00 |
hl ~ V2 |
||||
Методика определения области гидравлического сопротивления
1) Определить расход воды по формуле: Q = Wt , см3/с
2) Определить площадь живого сечения трубопровода по формуле: = ∙4 2, см2
3) Определить среднюю скорость движения воды в трубопроводе по формуле: = , см/с
4) Определить число Рейнольдса по формуле: = ∙
5) Вычислить относительную гладкость трубопровода:
∆э
6) Пользуясь данными табл. 1, определить область гидравлического сопротивления трубопровода.
Выполнение лабораторной работы
Потери напора по длине определяются в прямом горизонтальном трубопроводе 1 с
внутренним диаметром d=5,1 см на участке трубы длиной l = 500 см |
(рис. 1). По |
справочным данным эквивалентная шероховатость трубопровода э = 0,02 |
см. |
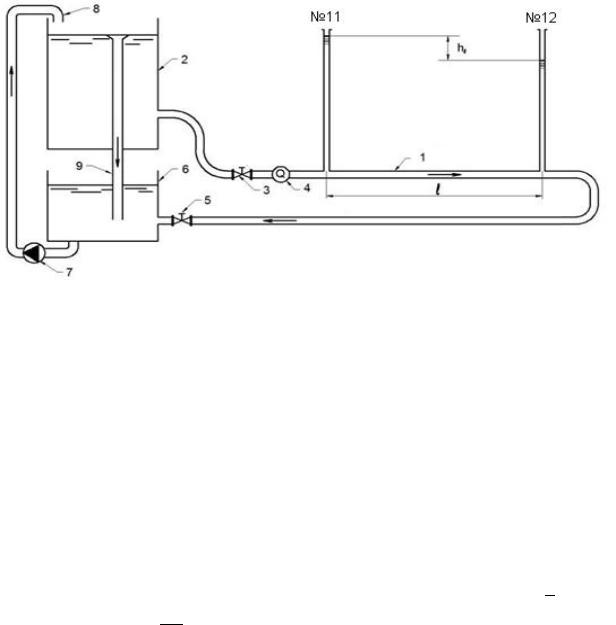
Вначале участка трубы установлен пьезометр № 11, в конце участка трубы установлен пьезометр № 12. Вода в трубопровод подается из питающего бака 2. Для определения расхода воды, проходящей по трубопроводу, установлен расходомер 4. Регулирование расхода воды в трубопроводе производится с помощью кранов 3 и 5.
После трубопровода 1 вода поступает в промежуточный бак 6. Система питания установки – оборотная, поэтому из бака 6 в бак 2 вода перекачивается по трубе 8 с помощью насоса 7. Уровень воды в баке поддерживается постоянным с помощью переливной трубы 9.
Вданной лабораторной работе определяется потеря напора по длине прямого горизонтального трубопровода (рис. 1) между сечениями 11-11 и 12-12 при напорном
движении.
Лабораторная работа «Потери напора по длине трубопровода» |
Стр. 7 |
Рис. 1. Схема установки для изучения потерь напора по длине потока
На участке 11—12 местные сопротивления отсутствуют. Поэтому hw = hl. Опытным путём потеря напора по длине трубопровода hl может быть определена как разность напоров в сечениях 11-11 и 12-12.
H |
11 |
H |
12 |
h |
|
|
l |
Выражение (6) представляет собой уравнение Бернулли
(8)
|
p |
|
V 2 |
|
p |
|
V 2 |
|
|
|
z11 |
11 |
|
11 11 |
z12 |
12 |
|
12 12 |
hw |
(9) |
|
|
2g |
|
2g |
|||||||
|
|
|
|
|
|
Для горизонтального трубопровода геометрические высоты во всех сечениях равны: z11=z12. Если плоскость сравнения 0-0 совпадает с осью трубопровода, а, следовательно, и с центрами тяжести живых сечений, то z11=z12=0.
Согласно уравнению неразрывности потока, расход Q во всех сечениях трубопровода одинаков. Площадь живого сечения потока ω тоже не изменяется по длине
потока. Следовательно, средняя скорость движения воды в трубопроводе = =
и скоростная высота 2 = , то есть, во всех живых сечениях одинаковы. Это
2
означает, что движение воды в трубопроводе равномерное. Таким образом,
z |
z |
; |
V |
2 |
|
V |
2 |
|||
|
|
|
|
|||||||
11 |
11 |
12 |
12 |
|||||||
|
|
|
|
|||||||
11 |
12 |
|
2g |
|
|
2g |
|
|||
|
|
|
|
|
|
|||||
(10)
и уравнение (9) преобразуется в выражение:
|
|
|
|
|
|
∙2 |
|
|
|
|
∙2 |
|
|
|
|
|||||||
|
|
= ( + |
|
11 |
+ |
11 |
|
11 |
) − ( |
|
+ |
12 |
+ |
12 |
12 |
) = |
11 |
− |
12 |
|
(11) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
11 |
|
|
2 |
12 |
|
|
|
2 |
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
которое показывает, |
что в |
прямом напорном |
трубопроводе |
п о т е р и |
н а п о р а |
п о |
||||||||||||||||
д л и н е опытным путём можно определить как разность пьезометрических высот в начале и в конце рассматриваемого участка. Иными словами, при равномерном движении жидкости потери напора можно определять не только по напорной, но и по пьезометрической линии.
Таким образом, при проведении лабораторной работы опытное определение hl заключается в измерении разности пьезометрических высот между пьезометрами №11 и №12 (рис. 1).
Формула (11) применяется в лабораторной работе для опытного определения коэффициента гидравлического трения:
Лабораторная работа «Потери напора по длине трубопровода» |
Стр. 8 |
|
2gd h |
|
l |
||
|
||
|
l V |
|
|
2 |
(12)
Чтобы воспользоваться формулой (12), необходимо определить расход воды в трубопроводе так же, как это делается в других лабораторных работах:
= |
|
(13) |
|
|
|||
|
|
по расходу вычислить среднюю скорость движения воды
= |
|
(14) |
|
|
|||
|
|
где ω – площадь живого сечения потока, = |
2 |
|
4 |
||
|
||
Обработка опытных данных |
|
1.Определение коэффициента гидравлического трения опытным путём: 1.1. Вычислить потерю напора по длине по формуле (11), см:
11 12
= −
1.2.Вычислить расход воды по формуле (13), см3/с: =
1.3.Вычислить среднюю скорость движения воды в трубопроводе по формуле (14),
см/с: = |
|
, где ω – площадь живого сечения потока, см: = |
2 |
|
|
4 |
|||
|
|
1.4. Вычислить коэффициент гидравлического трения опытным путём по формуле
(12): = |
2 ∙ ∙ |
∙2 |
g=9,81 м/с2=981 см/с2
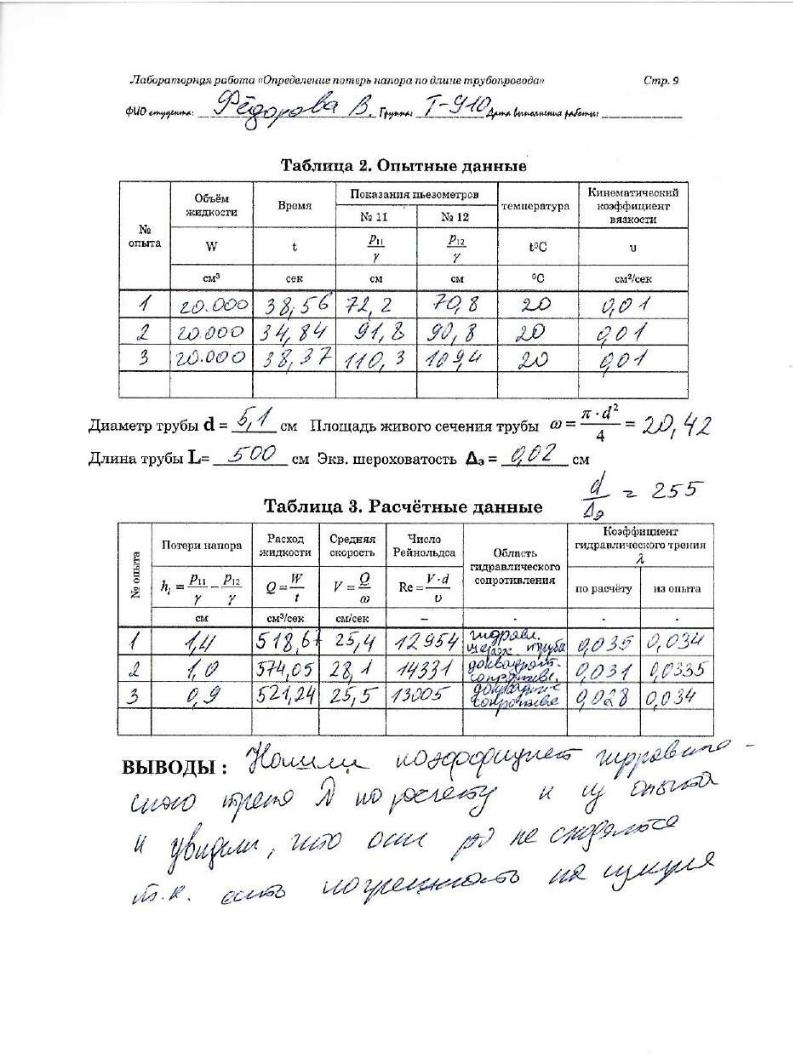
Все данные вычислений записать в табл. 3.
2.Определение коэффициента гидравлического трения по эмпирическим формулам (по расчёту):
2.1. Вычислить число Рейнольдса по формуле (5): = |
∙ |
|
|
||
|
2.2. Определить режим движения в трубопроводе (Reкр=2300).
2.3. Вычислить относительную гладкость трубопровода ∆э.
2.4. Пользуясь данными табл. 1, определить область гидравлического сопротивления трубопровода.
2.5. Определить эмпирическую формулу, соответствующую найденной области гидравлического сопротивления (см. табл. 1).
2.6. Вычислить значение коэффициента гидравлического трения по соответствующей эмпирической формуле (λ по расчёту).
Все данные вычислений записать в табл. 3.
3.Сделать выводы. В выводах сравнить коэффициент гидравлического трения λрасч., полученный по эмпирическим формулам с коэффициентом гидравлического трения λопыт., полученным опытным путём.

Лабораторная работа «Потери напора по длине трубопровода» |
Стр. 10 |
Лабораторная работа «ОПРЕДЕЛЕНИЕ ПОТЕРЬ НАПОРА ПО ДЛИНЕ ТРУБОПРОВОДА»
Вопросы к защите лабораторной работы
1.Какие виды потерь напора существуют?
2.Дайте определение «потери напора по длине трубопровода», приведите примеры (нарисовать). При каком виде движения жидкости возникают потери напора по длине?
3.Объясните значение и назовите единицы измерения величин, входящих в формулу Вейсбаха-Дарси: = ∙ ∙ 2
2
4.Что такое шероховатость? Нарисуйте и поясните понятия гидравлически гладкой и гидравлически шероховатой стенки.
5.Какие области гидравлических сопротивлений вам известны? Перечислите их, покажите зависимость их от числа Рейнольдса.
6.Как зависит коэффициент гидравлического трения от числа Рейнольдса
иэквивалентной шероховатости в различных областях гидравлического сопротивления.
7.Поясните понятие доквадратичной и квадратичной области сопротивления.
8.Как определить потери напора по длине трубопровода опытным путем?
9.Какими способами можно определить коэффициент гидравлического трения?
Литература
1)Чугаев, Р. Р. Гидравлика (техническая механика жидкости): учеб.для вузов – изд. 6-е, репринтное – М. : ООО «ИД «БАСТЕТ», 2013. – 672 с.: ил.
2)Моргунов, К.П. Гидравлика. [Электронный ресурс] — Электрон. дан. — СПб.: Лань, 204. — 288 с. — Режим доступа: http://e.lanbook.com/book/51930 — Загл. с экрана.
3)Гидравлика [Текст] : методические указания к лабораторным работам / , ФГБОУ ВПО ПГУПС, каф. "Водоснабжение, водоотведение и гидравлика"; сост. А. Б. Пономарев, Е.В. Русанова [и др.] ; под общ. ред. В. И. Штыкова. - Санкт-Петербург : ФГБОУ ВПО ПГУПС, 205. - 56 с. : ил.
