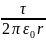Тема 2. Теорема Остроградского-Гаусса для электрического поля в вакууме

Из примера с диполем видно, что нахождение напряженности электрического поля, создаваемого любой схемой зарядов, исходя из принципа суперпозиции полей, является непростой задачей. Другой метод расчета основан на использовании теоремы Остроградского - Гаусса. Дадим определение потока вектора сквозь некоторую поверхность. Потоком напряженности электрического поля сквозь малый участок поверхности dS называется величина: .

Тогда для произвольной замкнутой поверхности поток вектора сквозь эту поверхность: (1.5)

При вычислении этого интеграла векторы нормалей к поверхности должны быть направлены в одну и ту же сторону по отношению к поверхности S. Будем считать нормали внешними (от поверхности, а не к ней).

Рис. 1.5.

Пусть электрическое поле создается точечным зарядом q. Рассмотрим произвольную замкнутую поверхность, охватывающую этот заряд. Поток напряженности сквозь элемент dS этой поверхности равен: , где

r – расстояние от элемента поверхности dS до заряда q.

Если электрическое поле создается системой зарядов, то, по принципу суперпозиции: , и

Ф = .

Можно показать, что если заряд находится не внутри, а снаружи замкнутой поверхности, то поток вектора напряженности сквозь эту поверхность равен нулю.

На основании вышесказанного, можно сформулировать теорему Остроградского – Гаусса: поток вектора напряженности электрического поля в вакууме сквозь произвольную замкнутую поверхность равен алгебраической сумме зарядов, заключенных внутри этой поверхности, деленной на .

Единица измерения потока вектора напряженности .

Применение теоремы Остроградского -Гаусса для расчета напряженности электростатического поля.

1. Поле равномерно заряженной бесконечной плоскости с поверхностно плотностью зарядов +.

Рис. 1.6.

Если плоскость помещена в среду с относительной ди­электрической проницаемостью , то напряженность электростатического поля, соз­даваемая плоскостью, равна .

Из формулы следует, что Е не зависит от расстояния между плоскостью и точкой на­блюдения, т.е. поле равномерно заряженной бесконечной плоскости является однородным.

2. Поле двух бесконечных разноименно заряженных плоскостей.

На рис. 1.7 перпендикулярно чертежу расположены две разноименно заряженные плоскости с поверхностными плотно­стями за­рядов + и -. Силовые линии плоскостей перпенди­ку­лярны им и параллельны между собой. Силовые ли­нии выходят из плоскости + и входят в плоскость ‑. На ри­сунке сплошными стрелками изо­бражено поле плоскости + и пунктирными - поле плоскости -.

Напряженности полей обеих плоскостей равны по абсолютной величине . Однако, справа и слева от плоскостей напряженности и направлены проти­во­положно, поэтому суммарная Е=0 и поле отсутствует. В области между плоскос­тями и направлены одинаково, поэтому

Рис.1.7.

.

3. Поле бесконечной заряженной нити.

Пусть имеется бесконечная заряженная нить, линейная плотность заряда которой равна τ. Из соображений симметрии, силовые линии поля, созданного нитью (линии напряженности) лежат в плоскости, перпендикулярной нити.

Рис. 1.8.

Е=