Никитина Дарья ПИН-21Д ЛР6

Лабораторная работа №6

Компьютерный практикум по математическому анализу

никитина дарья пин-21д

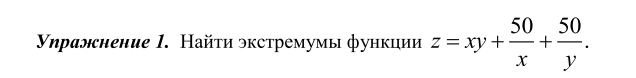
Текст программы

clear;clc; close all

% Практикум 7.Экстремумы функций двух переменных.

% Упражнение 1. (Upr_7_1.m)

y=linspace(3,4.5,20);

x=linspace(3,4.5,20);

[X, Y]=meshgrid(x,y);

Z=X.*Y+50./X+50./Y;

[C,h]=contour(X,Y,Z); grid

clabel(C,h,'FontSize',11, 'Color',[0 0 1])

set(h,'LineWidth',1,'LevelStep',0.2, 'TextStep',0.2)

title ('Линии уровней функции Z=xy+50/x+50/y');

xlabel('x'); ylabel('y')

figure

surfc(X,Y,Z) ;

xlabel('x'); ylabel('y');zlabel('z')

title ('График функции Z=xy+50/x+50/y');

[M, f]=fminsearch('F_2', [3.7,3.7]);

fprintf('Функция имеет минимум в точке ( x0=%5.4f ; y0=%5.4f)\n',[M(1) M(2)])

fprintf('Минимальное значение функции Zmin=%5.4f)\n',f)

hold on

plot3(M(1),M(2),f,'or','LineWidth',3)

hold off

view(33,33)

% Задание функции для поиска ее минимума 2-х переменных

function f=F_2(u)

f=u(1).*u(2)+50./u(1)+50./u(2);

Результат

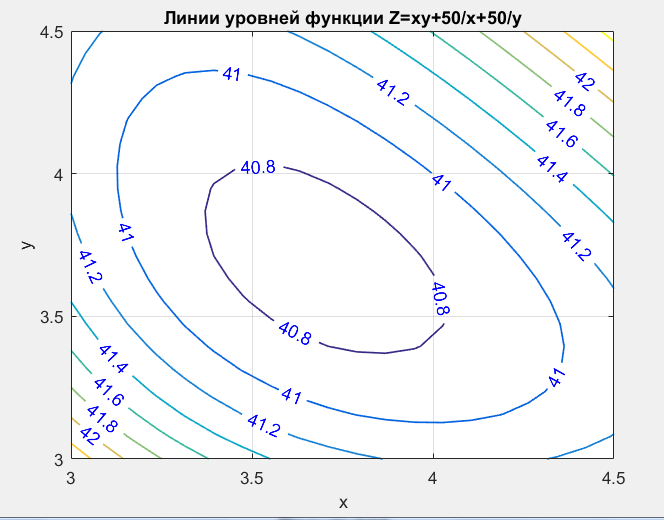
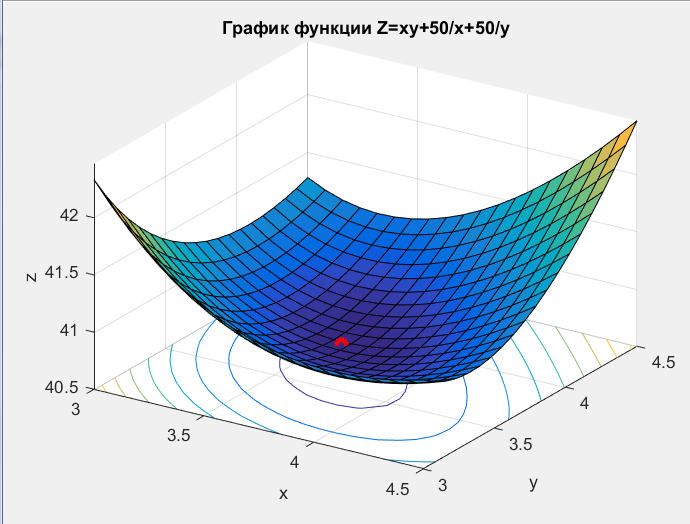
Функция имеет минимум в точке ( x0=3.6841 ; y0=3.6840)

Минимальное значение функции Zmin=40.7163)

Текст программы

clear;clc; close all

% Практикум 7.Экстремумы функций двух переменных.

% Упражнение 2,3. (Upr_7_2_3.m)

% Построение линий уровней функции

figure('Position',[100 50 500 550])

y=linspace(1,5,20);

x=linspace(0.2,3,20);

[X, Y]=meshgrid(x,y);

Z= X.^2+Y.^2-2*log(X)-18*log(Y);

subplot(2,1,1)

[C,h]=contour(X,Y,Z); grid

clabel(C,h,'FontSize',8, 'Color',[0 0 1])

set(h,'LineWidth',1,'LevelStep',1, 'TextStep',1)

title ('Линии уровней функции Z=X^2+Y^2-2*log(X)-18*log(Y)');

xlabel('x'); ylabel('y')

subplot(2,1,2)

% Построение поверхности

surf(X,Y,Z);

xlabel('x'); ylabel('y');zlabel('z')

title ('График функции Z=X^2+Y^2-2*log(X)-18*log(Y)');

view(-67,39)

% Поиск минимума функции 2-х переменных

[M, f]=fminsearch('F_1', [2,3]);

hold on

plot3(M(1),M(2),f,'or','LineWidth',3);% Точка минимума

hold off

fprintf('Функция имеет минимум в точке ( x0=%5.4f ; y0=%5.4f)\n',[M(1) M(2)])

fprintf('Минимальное значение функции Zmin=%5.4f\n',f)

disp(' ')

disp('Проверка необходимого и достаточного условия экстремума функции 2-х переменных')

disp(' ')

syms x y z

global z

z=x^2+y^2-2*log(x)-18*log(y);

[dzx, dzy, A]=Pr;% обращение к функции вычисляющей частные производные и

% минор матрицы Гессе

disp(' Первые частные производные и минор в символьном виде ')

disp([dzx, dzy])

disp(A)

x0=round(M(1),3);y0=round(M(2),3); % Точка минимума

disp('Численные значения 1-х частных производных в точке минимума')

dzx_n=subs(dzx,[x,y],[x0,y0])

dzy_n=subs(dzy,[x,y],[x0,y0])

D=subs(det(A),[x,y],[M(1), M(2)]);% Определитель минора

fprintf('Определитель минора =%5.4f\n',double(D))

% Задание функции для поиска ее минимума 2-х переменных

function f=F_1(u)

f= u(1).^2+u(2).^2-2*log(u(1))-18*log(u(2));

function [dzx, dzy, A]=Pr

% Вычисление частных производных 1-го и и

% и минора, состоящего из частных производных 2-го порядка

syms x y z

global z

dzx=diff(z,x);

dzy=diff(z,y);

A=[diff(z,x,2) diff(z,x,y); diff(z,x,y) diff(z,y,2)];

Результат

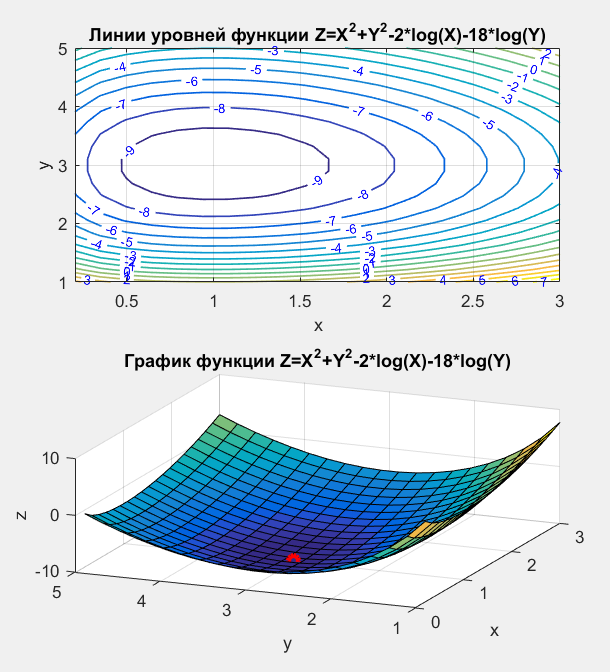
Функция имеет минимум в точке ( x0=1.0000 ; y0=3.0000)

Минимальное значение функции Zmin=-9.7750

Проверка необходимого и достаточного условия экстремума функции 2-х переменных

Первые частные производные и минор в символьном виде

[ 2*x - 2/x, 2*y - 18/y]

[ 2/x^2 + 2, 0]

[ 0, 18/y^2 + 2]

Численные значения 1-х частных производных в точке минимума

dzx_n =

0

dzy_n =

0

Определитель минора =16.0003

Текст программы

clear;clc; close all

% Практикум 7.Экстремумы функций двух переменных.

% Упражнение 4_5. (Upr_7_4_5.m)

syms x y z u

global u

u=x+y/x+z/y+2/z;

disp('Поиск экстремумов функции')

disp(u)

[dux, duy, duz, M1,M2,M3]=Pr3;% Обращение к функции Pr3

%Решение системы трех уравнений, суть которых

% необходимое условие экстремума функции 3-х переменных

solv=solve([dux==0,duy==0,duz==0],[x,y,z]);

disp(' Матрица решений системы. Каждая строка координаты (X,Y,Z) - стационарной точки')

R=[double(solv.x) double(solv.y) double(solv.z)];

disp(' ')

disp(R)

disp(' Определители трех угловых миноров матрицы Гессе в двух стационарных точках')

M1_n(1)=vpa(subs(M1,[x,y,z],[R(1,1),R(1,2),R(1,3)]));

M2_n(1)=vpa(subs(M2,[x,y,z],[R(1,1),R(1,2),R(1,3)]));

M3_n(1)=vpa(subs(M3,[x,y,z],[R(1,1),R(1,2),R(1,3)]));

M1_n(2)=vpa(subs(M1,[x,y,z],[R(2,1),R(2,2),R(2,3)]));

M2_n(2)=vpa(subs(M2,[x,y,z],[R(2,1),R(2,2),R(2,3)]));

M3_n(2)=vpa(subs(M3,[x,y,z],[R(2,1),R(2,2),R(2,3)]));

MR=[M1_n; M2_n; M3_n];

disp(' ')

disp(MR)

% Проверка условия минимума функции

if (MR(1,1)>0 & MR(2,1)>0 & MR(3,1) >0)

fprintf(' X=%5.3f; Y=%5.3f; Z=%5.3f - точка минимума\n',[R(1,1) R(1,2) R(1,3)])

Umin=double(subs(u,[x,y,z],[R(1,1), R(1,2), R(1,3)]));

fprintf('Минимальное значение функции Umin=%5.3f)\n',Umin)

end

% Проверка условия максимума функции

if (MR(1,2)<0 & MR(2,2)>0 & MR(3,2) < 0)

fprintf(' X=%5.3f; Y=%5.3f; Z=%5.3f - точка максимума\n',[R(2,1) R(2,2) R(2,3)])

Umax=double(subs(u,[x,y,z],[R(2,1), R(2,2), R(2,3)]));

fprintf('Минимальное значение функции Umax=%5.3f)\n',Umax)

end

function [dux, duy, duz, M1,M2,M3]=Pr3

% Вычисление частных производных 1-го и 2-го порядков

% и миноров матрицы Гессе, состоящего из частных производных 2-го порядка

syms x y z u

global u

% Символьное вычисление

dux=diff(u,x);

duy=diff(u,y);

duz=diff(u,z);

d2ux=diff(u,x,2);

d2uy=diff(u,y,2);

d2uz=diff(u,z,2);

duxy=diff(u,x,y);

duxz=diff(u,x,z);

duyz=diff(u,y,z);

M1=det(d2ux);

% Расчем миноров матрицы Гессе

M2=det([d2ux duxy;duxy d2uy ]);

M3=det([d2ux duxy duxz; duxy d2uy duyz; duxz duyz d2uz]);

Результат

Поиск экстремумов функции

x + y/x + z/y + 2/z

Матрица решений системы.Каждая строка координаты (X,Y,Z) - стационарной точки

1.1892 + 0.0000i 1.4142 + 0.0000i 1.6818 + 0.0000i

-1.1892 + 0.0000i 1.4142 + 0.0000i -1.6818 + 0.0000i

0.0000 + 1.1892i -1.4142 + 0.0000i 0.0000 - 1.6818i

0.0000 - 1.1892i -1.4142 + 0.0000i 0.0000 + 1.6818i

Определители трех угловых миноров матрицы Гессе в двух стационарных точках

[ 1.6817928305074292550048493299151, -1.6817928305074292550048493299151]

[ 1.5000000000000000364352828204649, 1.5000000000000000364352828204649]

[ 0.8408964152537147159115000574389, -0.8408964152537147159115000574389]

X=1.189; Y=1.414; Z=1.682 - точка минимума

Минимальное значение функции Umin=4.757)

X=-1.189; Y=1.414; Z=-1.682 - точка максимума

Минимальное значение функции Umax=-4.757)

>>