
- •Теоретические основы электротехники
- •Сопротивление провода кругового сечения при резком появлении поверхностного эффекта.
- •На основании закона полного тока:
- •Представим активное сопротивление R в форме:
- •Внешнее реактивное сопротивление определяется внешним магнитным потоком, который зависит от места расположения обратного
- •Неравномерное распределение синусоидального тока в плоском шинопроводе
- •Система из двух плоских проводящих шин
- •Учитывая соотношения между размерами, считаем электромагнитную волну плоской, все ее параметры
- •Определение постоянных интегрирования
- •Для контура l2, охватывающего левую шину и расположенного вплотную к ее поверхности ,
- •Используем полученное соотношение для анализа распределения тока по сечению шины. Определим плотность тока
- •Эквивалентная глубина проникновения
- •Активное сопротивление шины для переменного тока.
- •Определим активное сопротивление шины:
Теоретические основы электротехники
Теория электромагнитного поля
ВШВЭ проф. Л. И. Сахно 2021
1
Сопротивление провода кругового сечения при резком появлении поверхностного эффекта.
Постоянный ток (ω = 0) при протекании по проводнику распределяется по его сечению равномерно, т.е. плотность тока во всех точках сечения одинакова .
Поверхностный эффект возникает на переменном токе и считается «резким» если поперечные размеры проводника намного больше длины электромагнитной волны в этом проводнике.
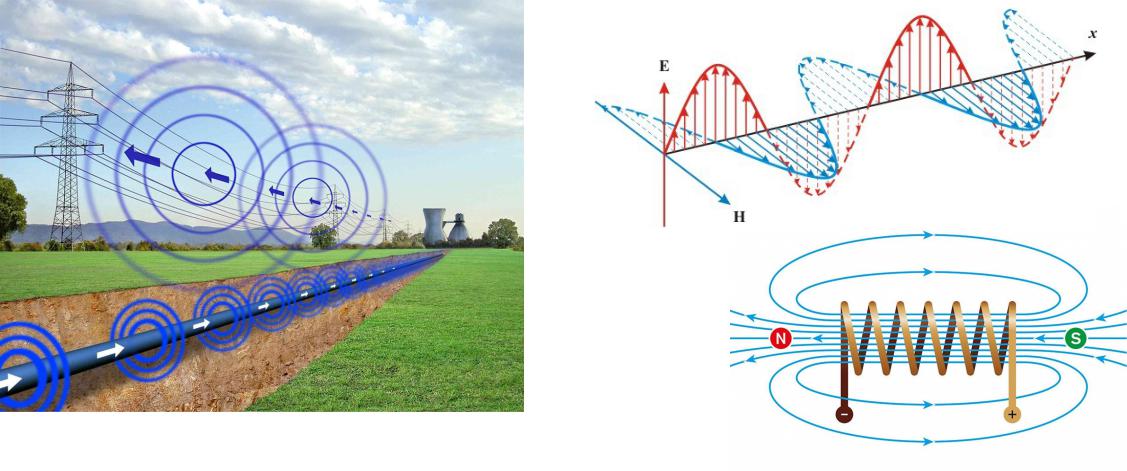
Рассмотрим случай кругового цилиндрического проводника с током . Если обратный провод удален на значительное расстояние, то поле прямого провода обладает цилиндрической симметрией.
 R R
R R
R
r |
r |
Электромагнитную волну в проводнике считаем плоской, если R>> .
В этом случае комплексы напряженности электрического и магнитного поля на поверхности проводника связаны соотношением:
Проникая внутрь проводника, электромагнитная волна затухает, следовательно, плотность тока на поверхности максимальна и уменьшается к центру проводника
Напряжение на участке проводника длиною l определяется из соотношения:
Так как поле плоскопараллельное, то во всех точках вдоль оси проводника напряженность электрического поля на поверхности одинакова, тогда:
На основании закона полного тока:
радиус провода (вместо R на рисунке на слайде 2)
и в силу осевой симметрии поля можем записать для комплексов:
Отношение напряжения к току позволит определить комплексное сопротивление проводника. Оно состоит из вещественной части - активного сопротивления R и мнимой части - реактивного сопротивления, которое определяется лишь магнитным потоком в теле проводника – т.е. внутренним магнитным потоком или внутренней индуктивностью. Это сопротивление называется внутренним реактивным сопротивлением – Xвнутр.. Комплексное
внутреннее сопротивление определяется соотношением:
Представим активное сопротивление R в форме:
s/ – эквивалентное сечение проводника, определяющее его активное сопротивление на переменном токе при резком
поверхностном эффекте. Площадь сечения равна площади кольца длиной 2 r и шириной, равной , которая называется эквивалентной глубиной проникновения и определяется из соотношения:
=
На эту глубину реально проникает в проводник электромагнитное поле, и в основном по этому сечению идет переменный ток. Учитывая, что длина волны в проводящей среде определяется выражением:
,можем записать: =
– эквивалентная глубина проникновения примерно в 6 раз меньше длины волны
впроводнике.
Внешнее реактивное сопротивление определяется внешним магнитным потоком, который зависит от места расположения обратного провода. Отношение активного сопротивления провода кругового сечения на переменном токе к сопротивлению этого же проводника на постоянном токе равно:
Для проводников произвольной формы сечения отношение сопротивлений равно:
s - сечение, а u - периметр проводника
Неравномерное распределение синусоидального тока в плоском шинопроводе
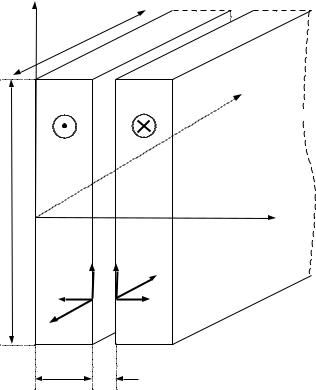
Система из двух плоских проводящих шин
Шины расположены параллельно на достаточно малом расстоянии друг от друга, В шинах протекает переменный синусоидальный ток – i.
y |
|
l |
|
|
|
|
|
|
x |
h |
|
i |
i |
|
|
0 |
|
z |
|
|
|
|
||
|
S |
Hy |
Hy |
Ex |
|
E |
|
S |
|
|
|
|
|
|
|
x |
d |
|
|
|
|
|
|
l >> h >> d >>
Высота шин h , ширина d
Учитывая соотношения между размерами, считаем электромагнитную волну плоской, все ее параметры
зависят только от одной координаты z. Воспользуемся решением уравнений для плоской синусоидальной волны .
(1)
– корень характеристического уравнения
Для нахождения постоянных А1 и А2, используем граничные условия. Начало координат расположим на наружной поверхности левой шины, и определим значения напряженности магнитного поля при z1 = 0 и при
z2 = d. Рассматривая совокупность двух соседних шин с одинаковыми по величине и противоположными по направлению токами, применим закон полного тока.

Определение постоянных интегрирования
Для контура l1 , охватывающего обе шины с прямым и обратным током и расположенного вплотную к поверхностям обеих шин , получим:
Считаем, что снаружи, вне системы шин, магнитное поле отсутствует, т.е. при z1 = 0
А1 + А2 = 0, |
А1 = – А2 = А. |
l1 l2
