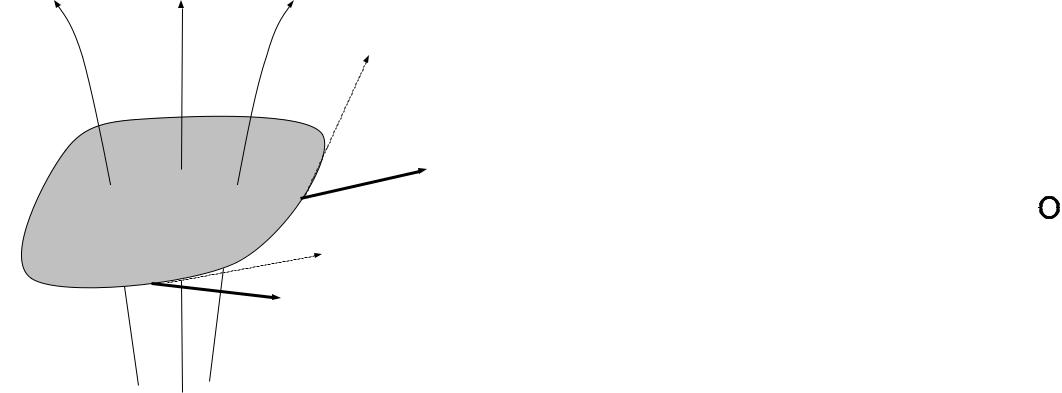
Определение магнитного потока через векторный потенциал
B rot A
dl |
Применим теорему Стокса: |
|
|
|
A |
|
|
|
l |
S |
dl |
Bds |
rot A ds A dl |
|
|
|
S |
S |
l |
|
|
|
A |
|
|
|
Граничные условия для векторного потенциала
При рассмотрении граничных условий из интегралов по замкнутым контурам для векторов поля мы получали на поверхности раздела сред равенство касательных составляющих векторов. По аналогии можем записать:
A1 = A2
На поверхностях раздела различных сред не изменяются ни нормальные, ни касательные составляющие векторного магнитного потенциала. Это означает, что при переходе из одной среды в другую векторный
магнитный потенциал не изменяется ни по величине, ни по направлению.
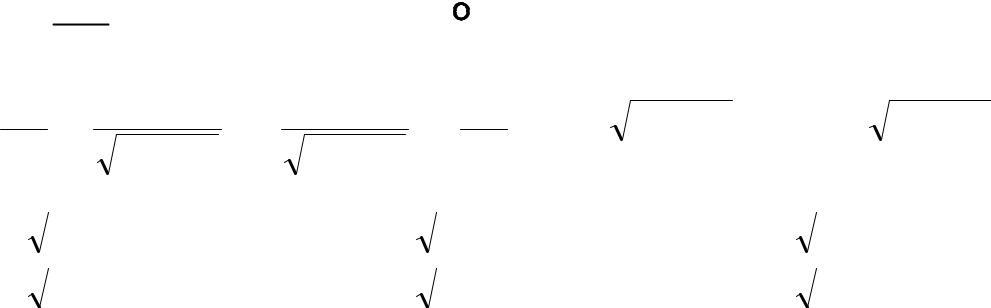
Пример
Определим магнитный поток, сцепляющийся с прямоугольной рамкой, расположенной в одной плоскости с прямолинейным проводником с током, причем две стороны рамки параллельны проводнику с током
i |
|
|
0 |
dz |
z |
|
|
|
|||
|
|
|
|
r1 |
|
– L |
a |
b |
+ L |
||
|
A |
r2 |
|||
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
1 |
A |
|
l |
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
A2 |
|
|
|
|
|
h |
|
|
|
|
0 i |
|
dz |
|
|
|
A dl h( A1z A2z ) |
|
|
|
|
|||||
|
A Az |
|
|
|
|
|
|
|
|
|
l |
|
|
|
|
|
||
|
4 z |
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
0i ln( z |
|
|
|
|
|
|||
|
|
0i |
L |
|
2dz |
|
L |
|
2dz |
|
|
|
|
|
L |
|
||
A1 |
A2 |
|
z |
2 |
|
z |
2 |
|
z2 a2 ) ln( z |
z2 |
b2 |
) L |
|
|||||
|
|
4 |
L |
|
a |
|
L |
b |
|
|
4 |
|
|
|
|
|
||
|
|
z |
|
|
|
L |
|
|
z |
|
|
|
L |
|
0i |
|
|
|
|
a |
||||
|
0i |
z 2 |
a2 |
|
0i |
z 2 |
a2 |
|
L |
L2 |
a2 |
|||||||||||||
|
|
ln |
|
|
|
|
|
2 |
|
ln |
|
|
|
|
|
|
|
ln |
|
|
|
ln |
|
|
4 |
z |
|
|
|
4 |
z |
|
|
|
2 |
|
|
|
b |
||||||||||
z 2 |
b2 |
z 2 |
b2 |
L |
L2 |
b2 |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
L |
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
||
A1 A2 |
|
|
0i |
ln |
b |
|
|
i h |
|
b |
|
|
|
|
|
|
0 |
|
ln |
|
|||
2 |
a |
|
|
||||||||
2 |
a |
||||||||||
|
|
|
|
|
|||||||
Простота вычисления магнитных потоков с помощью векторного потенциала позволяет успешно использовать векторный магнитный
потенциал для расчета собственных и взаимных индуктивностей
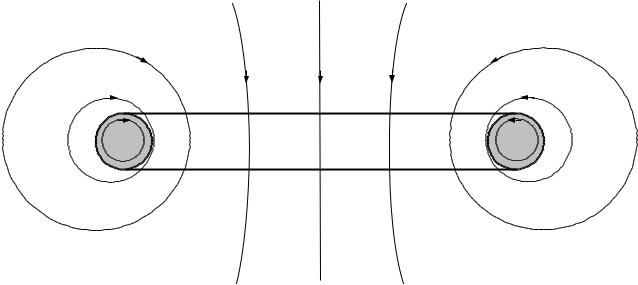
Расчет индуктивностей. Общие выражения для взаимной и собственной
Выраженияиндуктивностейдля индуктивностей будем получать в предположении, что в проводниках протекают равномерно распределенные по сечению постоянные токи. Предварительно введем понятие о внешнем и внутреннем магнитном потоке
1 |
2 |
3 |
4 |
5 |
6 |
|
|
|
|
|
Часть трубок магнитного потока (1 – 6), сцепленных с витком, не проходит сквозь проводник с током, а поток, созданный этими трубками называется внешним магнитным потоком. Трубки магнитного потока, проходящие сквозь материал проводника, сцепляются только с частью тока в проводнике и создают магнитный поток, называемый внутренним магнитным потоком.
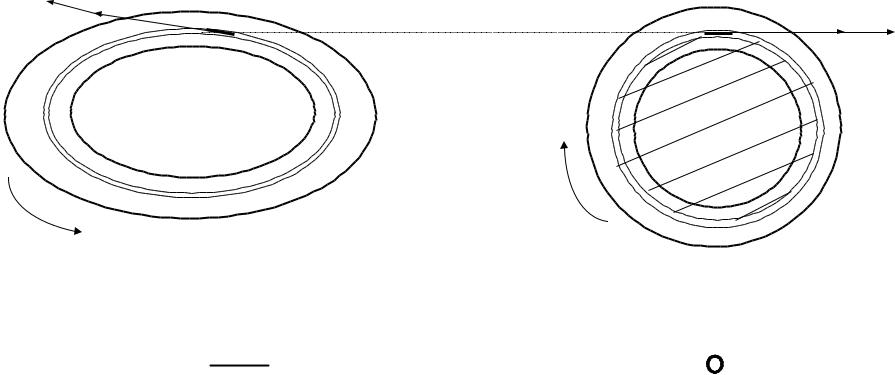
Индуктивности массивных контуров
Определение взаимной индуктивности между двумя массивными контурами.
J1 |
d |
|
|
|
|
|
r |
|
J2 |
d |
|
|
l1 |
|
|||
|
|
|
|
l2 |
|
|
|
|
|
|
|
|
|
1 |
l2 |
2 |
|
|
|
|
|
i2
i1
M 21 |
|
|
A dl |
|
||
21 |
i1 |
|
21 |
|
2 |
2 |
|
|
|||||
|
|
|
l2 |
|
|
|
Элементарное потокосцепление с трубкой тока во втором контуре определяется отношением тока в этой трубке к полному току второго контура:
d di2 |
di2 |
|
|
||||
A dl |
|
||||||
21 |
i |
21 |
i |
|
2 |
|
2 |
|
|
|
|
||||
|
2 |
|
2 |
l2 |
|
|
|
|
1 |
|
|
|
|
i |
|
|
|
||
|
( A2 dl2 )( J 2 ds2 ) |
||||
|
2 |
l |
|
|
|
|
|
2 |
|
|
|
|
1 |
|
|
|
|
i |
|
|
|
||
|
( A2 J 2 )( dl2 ds2 ) |
||||
|
2 |
l |
|
|
|
|
|
2 |
|
|
|
Полное потокосцепление взаимоиндукции второго контура получим, проинтегрировав полученное выражение по всем трубкам тока во втором контуре, т.е. всему объему второго контура:
|
|
1 |
|
|
|
|
|
( A J )( |
|||||
21 |
|
i |
|
2 |
2 |
|
|
|
|
|
|||
|
|
2 |
S |
l |
|
|
|
|
|
2 |
2 |
|
|
|
1 |
|
|
|
dl2 ds2 ) |
|
|
|
|
i |
|
|
||
|
( A2 J 2 )dv2 |
|||
|
2 V2 |
|
|
|
Величина векторного магнитного потенциала в точках второго контура определяется с помощью полученного ранее решения уравнения Пуассона для векторного магнитного потенциала через плотность тока в первом контуре:
|
0 J1dv1 |
|||
A |
|
|||
|
2 |
|
|
|
|
4 V r |
|||
|
|
|||
|
|
1 |
|
|
Тогда потокосцепление взаимоиндукции второго контура можем представить в виде:
|
0 |
|
|
J1dv1J 2 dv2 |
|
0 |
|
|
J1J 2 dv1dv2 |
||
21 |
4 i |
|
r |
|
4 i |
|
r |
||||
|
|
|
|
|
|
|
|
|
|
|
|
2 V V |
2 |
|
|
|
2 V V |
2 |
|
|
|||
|
|
|
|
|
|
||||||
|
|
1 |
|
|
|
|
1 |
|
|
||
Взаимная индуктивность между вторым и первым контуром можно вычислить из соотношения:
M 21 |
|
21 |
|
0 |
|
|
J1J 2 dv1dv2 |
|
i |
4 i i |
|
|
|||||
|
|
|
|
r |
||||
|
|
1 |
|
1 2 V V |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
При определении взаимной индуктивности между первым и вторым контуром необходимо определить потокосцепление первого контура, задав ток во втором контуре. Проделав аналогичные вычисления, получим:
|
0 |
|
|
|
J1J 2 dv1dv2 |
M |
12 |
|
0 |
|
|
J1J 2 dv1dv2 |
M |
|
|||
4 i |
|
r |
|
4 i i |
|
|
|
||||||||||
12 |
12 |
i |
|
|
|
r |
|
21 |
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
1 V |
V |
2 |
|
|
|
|
2 |
|
1 2 V V |
2 |
|
|
|
|
||
|
|
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
||
Таким образом, взаимная индуктивность между двумя контурами получается одинаковой, независимо от порядка ее вычисления, т.е. соблюдается принцип взаимности. Взаимная индуктивность не зависит от токов в контурах, так как плотности токов, стоящие в числителе, изменяются пропорционально токам контуров, стоящим в знаменателе. Взаимная индуктивность зависит от формы, размеров и взаимного расположения двух контуров и от распределения токов по сечению контуров.
Определение собственной индуктивности массивного контура. При определении собственной индуктивности применим полученную формулу для расчета взаимной индуктивности двух одинаковых, совмещенных друг с другом контуров. В этом случае токи в контурах совпадают (i1 = i2 = i), объемы контуров одинаковы (V1 = V2 = V), а
взаимная индуктивность переходит в собственную индуктивность (M12 L):
L |
|
0 |
|
|
JJ \dvdv\ |
|
4 i |
2 |
|
r |
|||
|
|
V V \ |
|
|||