Нетрудно заметить, что постоянство pv idem
приводит к условию |
p1 |
v2 |
|
|
|
|
|
|
|
|
v |
|
p |
2 |
|
|
|
1 |
|
Поэтому, в изопотенциальном процессе численные
значения термодинамической и потенциальной работ равны между собой. v p
l1,2 w1,2 pv ln v2 pv ln p1
1 2
Для идеального газа pv=RT=idem (изотермический)
l1,2 w1,2 RT ln v2 RT ln p1 v1 p2
Количество теплоты, подведенной к рабочему телу или отведенной от него в изопотенциальном процессе определяется из выражения первого начала термодинамики по балансу рабочего тела
q1,2 u l1,2 h w1,2
Для идеалного газа du=0; dh=0
q1,2 RT ln v2 RT ln p1 v1 p2
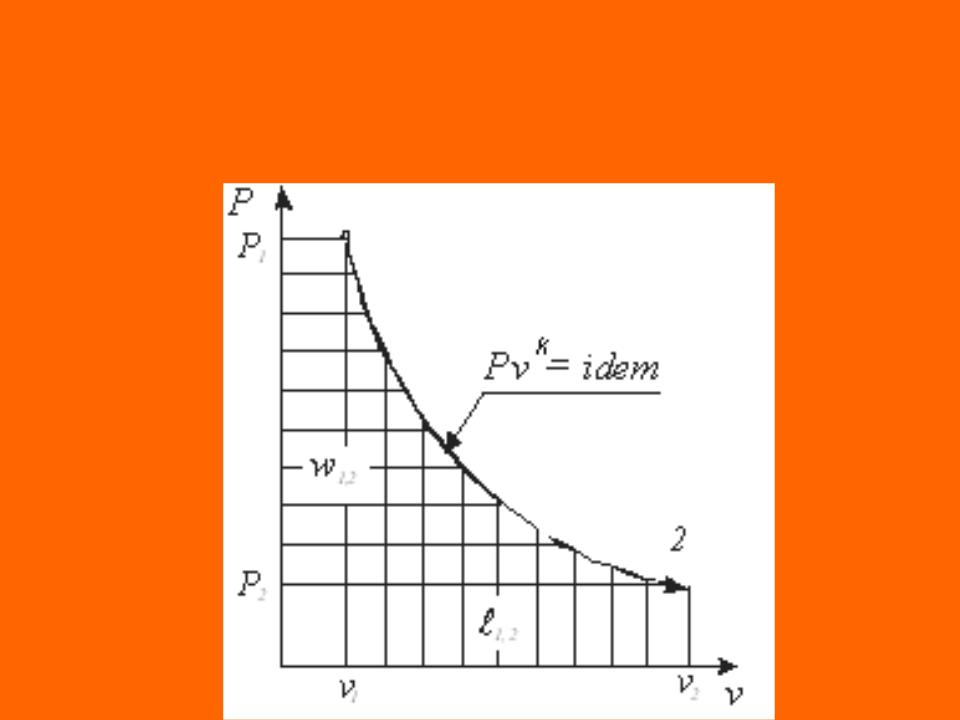
Адиабатный процесс - термодинамический процесс
изменения состояния системы, при котором отсутствует теплообмен q 0 и в силу обратимости процесса энтропия остается величиной постоянной s idem
Из выражения первого начала термодинамики для
простого тела при условии |
q 0 |
имеем |
|
s |
|
|
|
|
idem |
|
q q* q** du pdv dh vdp 0
Отсюда следует выражение для показателя адиабатного процесса
dh |
vdp |
ns k |
du |
pdv |
|
где ns=k – показатель адиабаты.
Расчетное выражение для расчета показателя адиабатного процесса
|
dp |
|
|
|
|
|
ns k |
p |
|
d ln p |
|
d log p |
. |
dv |
d ln v |
|
||||
|
|
|
d log v |
|||
|
v |
|
|
|
|
|
|
|
|
После интегрирования при условия постоянства |
|||||||||
показателя процесса имеем |
|
|
|
log |
p1 |
|
|||
|
|
|
|
w1,2 |
|
||||
ns |
k |
h |
|
|
p2 |
|
|||
u |
l1,2 |
|
v2 |
||||||
|
|
|
|
|
|||||
|
|
|
|
|
|
log v1 |
|||
Для идеального газа показатель адиабаты равен
k= cp/cv
Из уравнения адиабатного процесса получим выражение для связи параметров состояния
|
k log v2 |
log |
|
p1 |
, |
|||||
|
|
|
||||||||
|
|
|
v |
|
|
|
|
p |
2 |
|
потенцируя имеем |
1 |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|||
|
p2 |
|
k |
|
|
|
1 |
|
|
|
|
|
|
|
|
k |
|
|
|||
|
v2 |
v2 |
|
p2 |
|
|
1 |
|||
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
p1 v1 |
|
v1 p1 |
|
|
|
|
|||
pvk idem; |
|
1 |
|
|
|
|
||||
|
p k v idem; |
|||||||||
Выражения конечных (интегральных) величин термодинамической и потенциальных работа в адиабат- ном процесс можно получить при сопоставлении их
элементарных значений
l pdv,..... w vdp
l w pdv vdp d pv
С учетом определения показателя адиабаты имеем:
l w 1 k l d pv
l |
1 |
|
d pv |
|
1 |
k |
|||
|
|
Интегрируя последнее выражение с учетом того, что k=idem, получим интегрального уравнения термодинамической работы
|
2 |
1 |
|
|
1 |
|
|
|
|
|
|
|
l |
|
|
d( pv ) |
|
|
( p v p v ) u u |
2 |
|||||
|
|
|
|
|||||||||
1,2 |
1 1 |
k |
|
1 |
k |
1 |
1 |
2 |
2 |
1 |
||
|
|
|
|
|
|
|
|
|||||
Введем понятие характеристики процесса расширения или сжатия
1,2 p2v2
p1v1
Окончательно имеем уравнения для определения термодинамической и потенциальной работы
l1,2 |
p1v1 |
|
|
1 1,2 u1 u2 |
|||||||||||
k 1 |
|||||||||||||||
|
|
|
|
|
1 1,2 |
h1 h2 |
|||||||||
w1,2 kl1,2 |
k |
|
|
|
|
p1v1 |
|||||||||
k |
1 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|||||||
Различные уравнения для определения характе- |
|||||||||||||||
ристики расширения или сжатия 1,2 |
определяются с |
||||||||||||||
учетом уравнения адиабаты |
|
|
|
|
|||||||||||
|
p2v2 |
|
|
|
p2 |
k 1 |
|
|
k 1 |
||||||
|
|
|
k |
|
|||||||||||
|
|
|
|
|
|
v1 |
|
|
|||||||
|
|
|
|
|
|
||||||||||
|
p v |
|
p |
|
|
|
|||||||||
|
|
|
v |
1,2 |
|||||||||||
1 1 |
|
|
|
|
1 |
|
2 |
|
|
||||||
Применительно для идеального газа имеем:
l1,2 |
|
RT1 |
|
1 1,2 cvm t1 t2 |
||||
k 1 |
||||||||
|
|
|
|
|
|
|||
|
w1,2 kl1,2 |
k |
|
|
R1T1 1 1,2 cpm t1 t2 |
|||
|
k |
1 |
||||||
|
|
|
|
|
||||
T2 |
|
p2v2 |
|
p2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
p v |
p |
||||
|
|
|||||
1 |
|
1 1 |
|
1 |
|
k 1 |
|
k 1 |
|
|
k |
|
|||
|
|
v1 |
|
|
|
|
|||
|
|
|
||
|
v |
1,2 |
||
|
2 |
|
|
|