32. Криволинейные интегралы I рода

– интегральная сумма для функции f(x;y) по кривой AB.

Если существует конечный предел интегральный суммы при стремлении к нулю наибольший из всех длин дуг, не зависящее от способа разбиение кривой AB и выбора точек M_i, то он называется криволинейным интегралом первого рода от функции f(x;y) по кривой AB.

Где s – длина дуги кривой.

Направление кривой роли не играет:

Аналогично для пространственных кривых:

Геометрический смысл

Если f (x y) ≥0, то криволинейный интеграл 1 рода численно равен S части цилиндрической поверхности, у которая направляющая k лежит в плоскости XOY, а образующие — перпендикулярны ей.

Свойства криволинейного интеграла

4. k=k1+k2, тогда

33. Вычисление площади фигуры, ограниченной замкнутым контуром.

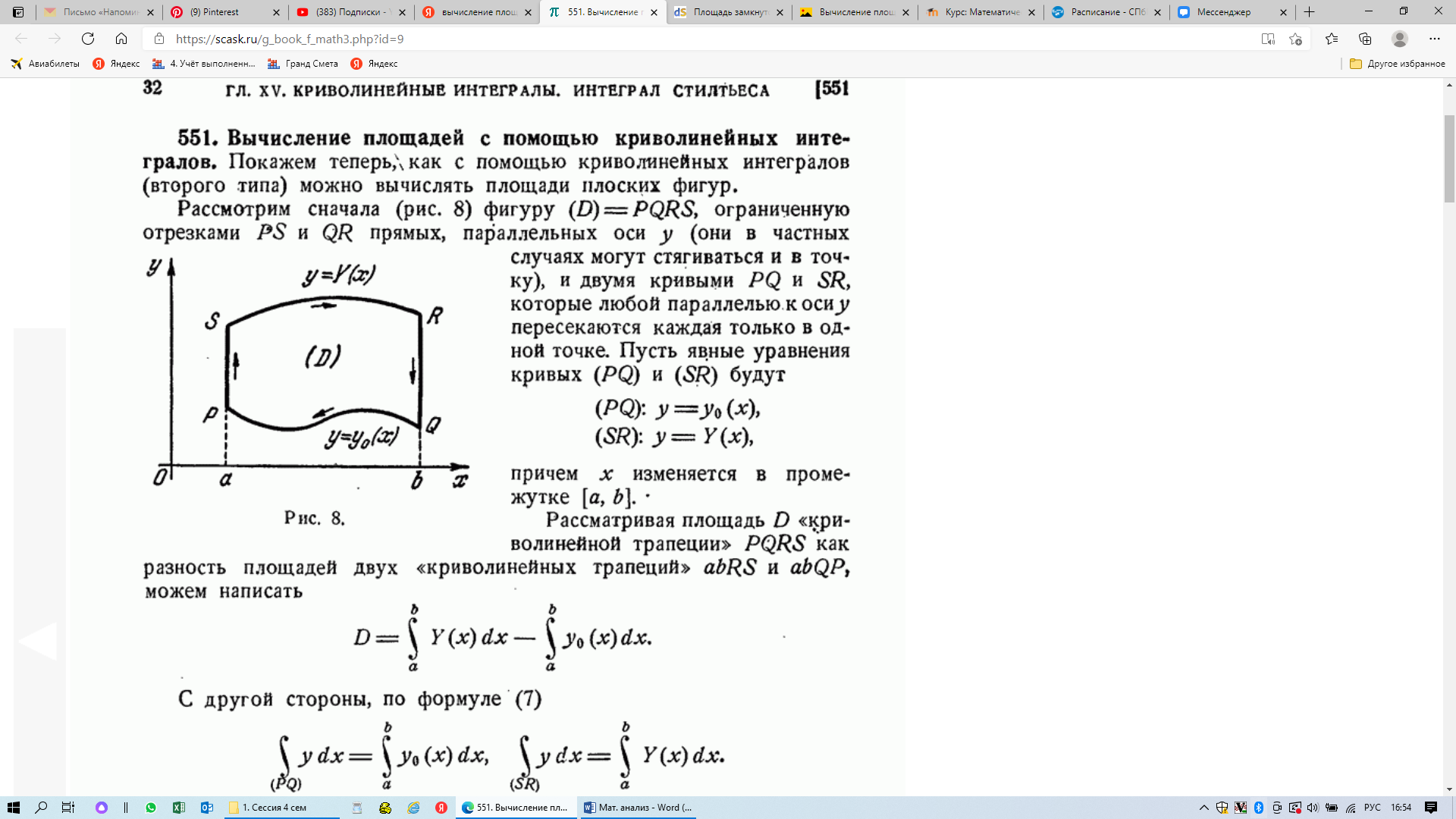
Контур интегрированной фигуры пробегается так, что ограниченная им область остается слева (положительное направление).