15. Интервал и радиус сходимости степенного ряда. Определение, формулы для вычисления.

Из теоремы Абеля (см. б. 14) следует, что существует такое число R > 0, что при I х| < R ряд сходится, а при I х| > R — расходится.

Число R получило название радиуса сходимости, а интервал (-R; R) — интервала сходимости степенного ряда. На концах интервала сходимости, т.е. при х = -R и x = R, ряд может как сходиться, так и расходиться.

Замечание. Если R = +∞, то интервал сходимости – вся числовая прямая (вся ось Ох). Если R = 0, то степенной ряд сходится лишь в точке х=0.

Нахождение интервала сходимости по признаку Доламбера

Рассмотрим ряд, составленный из абсолютных величин его членов:

, в котором все коэффициенты Сn, по крайнем мере, начиная с некоторого номера n, отличны от нуля.

По признаку Доламбера ряд сходится, если

будет меньше 1, т.е.

Если этот предел существует, то он и является радиусом сходимости ряда, т.е.

Интервал сходимости (-R;R).

Замечание. При исследовании сходимости на концах интервала сходимости для получающегося ряда с положительными членами применять признак Даламбера не имеет смысла, так как в этом случае всегда будем получать ,с нерешенным вопросом о сходимости ряда; в этом случае рекомендуется рассматривать другие признаки сходимости (например, признак сравнения, необходимый признак и т.д.).

16. Разложение функции в степенной ряд

(дальше про ряд Тейлора и Маклорена – б. 17)

17. Ряды Тейлора и Маклорена. Достаточное условие разложения функции в степенной ряд

Ряд вида называется рядом Тейлора для функции f(x) в точке a.

Рядом Тейлора функции f(x) называется ряд, коэффициенты которого определяются по формулам:

, т. Е. ряд

Ряд Телора со степенями х (а/х0=0) называют рядом Маклорена

Теорема. Для того чтобы ряд Маклорена сходился к функции f(x), необходимо и достаточно, чтобы при п -> ∞ остаток ряда стремился к 0, т.е. для всех значений х из интервала сходимости ряда.

Если функция f(x) разложима в ряд Маклорена, то это разложение единственное.

Разложение в ряд Маклорена некоторых функций

1. y =e^x

2. у =sin(х)

3. у = cos(х)

Рассматривая аналогично:

4. у = (1 + х)^m, где m — любое действительное число.

18. Разложение элементарных функций в степенной ряд

19. Использование степенных рядов для приближенных вычислений

Степенные ряды имеют самые разнообразные приложения.

С помощью степ. рядов вычисляют с заданной степенью точности:

• Значение ф-ий;

• Пределов функции

• Значение определённых интегралов (не берущихся) сложных, а также интегрируются;

• Приблеженные решения Дифференциальных уравнений;

Для нахождения с заданной точностью используют следствие из теоремы Лейбница: Погрешность при приближенном вычислении суммы сходящегося ряда, удовлетворяющего условия признака Лейбница*, по абсолютной величине не превышает абсолютной величины первого отброшенного члена. |C_n| ⩽ U_n+1

*Признак Лейбница. Если члены знакочередующегося ряда убывают по абсолютной величине и предел n-ого члена, при n-> , равен нулю, то ряд сходящийся, а его сумма по абсолютной величине не превосходит первого члена ряда.

20. Тригонометрический ряд: определение, основные свойства.

На ряду с системами степеней в элементарной математике хорошо изучены системы тригонометрических функций (2) cos x, sin x, cos 2x, sin 2x и т.д.

Тригонометрическим рядом называется функциональный ряд вида + nx + 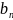sin nx), где an, bn, x ∈ R.

Ряд такого вида – тригонометрический ряд.

Идея принадлежит Жану Батисту Фурье

f(x) = + ( cos x + sin x) + ( cos 2x + sin 2x) + … + ( cos nx + sin nx) + … = + nx + sin nx)

Свойства тригонометрического ряда

1. Все ф-ии тригонометрической системы явл периодическими с периодом 2 , следовательно, если ряд сход. на отрезке (-π; π), то он сход на всей числовой прямой

Тригонометрическая система функций ортогональна на отрезке [−π; π].

21. Ряд Фурье. Теорема Дирихле.

Если функция f(x) заданная и непрерывная на отрезке (-π; π) разлагается в тригонометрический ряд, то коэффициенты разложения определяются единственным образом

Эти коэффициенты называются коэффициентами Фурье

Таким образом тригонометрический ряд – ряд Фурье.

22. Ряды Фурье для четных и нечетных функций.

Из определения четной и нечетной ф-ии следует:

Если f(x) – четное, то =

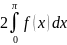
Если f(x) – нечетное то

Итак, если f(x) – четная, то ряд содержит только cos

(ТАМ ГДЕ К – это n)

Если f(x) – нечетная, то ряд содержит только sin

23. Ряд Фурье для функции с произвольным периодом

Пусть f(x) – периодическая ф-ия с периодом 2L (2L≠2π), тогда разложение ряда Фурье имеет вид:

Коэффициенты:

24. Разложение в ряд Фурье непериодической функции

Пусть ф-ия f(x) задана на отрезке [0; L], дополняем определение этой функции на отрезке [-L; L] (сохраняя кусочную монотонность), при этом можно разложить данную ф-ию в ряд Фурье:

Если f(x)= f(-x), то четным образом (cos)

Если f(-x)= - f(x), то нечетным образом (sin)

Итак, если f(x) – четная, то ряд содержит только cos

Если f(x) – нечетная, то ряд содержит только sin

25. Понятие двойного интеграла и его геометрическая интерпретация.

Функция z = f (х, у) называется интегрируемой на множестве D, если существует конечный предел I интегральной суммы этой функции на D при условии d -> 0.

Само значение предела I называется двойным интегралом функции z = f ( x , у) на множестве D. Обозначается двойной интеграл следующим образом:

Геометрический смысл двойного интеграла

Если функция f(x;y) непрерывна и неотрицательна в области D, то двойной интеграл представляет собой объем прямого цилиндрического тела (цилиндроида), построенного на области D как на основании и ограниченного сверху поверхностью z = f(x, у). Если f(х, у)=1 для всех (х, у)∈D, то I численно равен площади области D.

О бласть D, вырезаемая цилиндрическим брусом на плоскости Оху, называется основанием цилиндра, а цилиндрическая поверхность - его боковой поверхностью.

Теорема. Если функция z = f(х , у) непрерывна на элементарном множестве D, то

Интеграл, стоящий в правой части формулы, называется повторным интегралом и обычно записывается в виде