11. Абсолютная и условная сходимость знакопеременного ряда

Ряд называется абсолютно сходящимся, если сходится как сам ряд, так и ряд, составленный из абсолютных величин его членов.

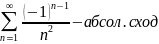
Ряд называется условно сходящимся, если сам ряд сходится, а ряд, составленный из абсолютных величин его членов, расходится.

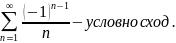
Замечание:

Различие между абсолютным и условно сходящимся рядом в следующем:

Абсолютно сходящие ряда в силу того, что их члены быстро убывают, а условно сходятся в результате того, что положительные и отрицательные слагаемые уничтожают друг друга.

12. Свойства абсолютно и условно сходящихся рядов: теорема Коши, теорема Римана

Свойства абсолютно и условно сходящихся рядов существенно отличаются:

1. если ряд 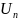сходится и есть С-const, то 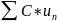– сходится абсолютно

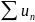2. если и 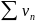сходятся абсолютно => сходится абсолютно

Теорема Коши: если сходится абсолютно, то он является абсолютно сходящимся при любой перестановке его членов, но при этом S не зависит от порядка его членов

Теорема Римана: если сходится условно, то какое бы не задать число А, можно переставить члены ряда так, чтобы сумма ряда оказалась равной числу А. Более того, можно так переставить члены условно сходящегося ряда, что ряд, полученный в результате перестановки, окажется расходящимся.

13. Функциональный ряд, его точка и область сходимости.

Функциональный ряд – это ряд, каждым членом которого является функция (не число).

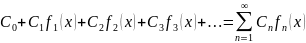
Равномерная сходимость функционального ряда:

1. Совокупность значений X, при которой функциональный ряд сходится, называется областью сходимости этого ряда. Функция S(x)= называется суммой ряда, а разность 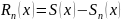называется остатком ряда.

2. Функциональный ряд называется равномерно сходящимся на отрезке , если для любого Е>0 можно найти такой номер N, что при всех n>N и для любого Х из будет выполнено неравенство

Признак равномерной сходимости. Функциональный ряд сходится абсолютно и равномерно на отрезке , если существует числовой сходящийся ряд с положительными числами такой, что

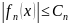
https://function-x.ru/rows3.html

14. Степенной ряд. Теорема Абеля и следствие из нее.

Совокупность тех значений х, при которых степенной ряд сходится, называется областью сходимости степенного ряда.

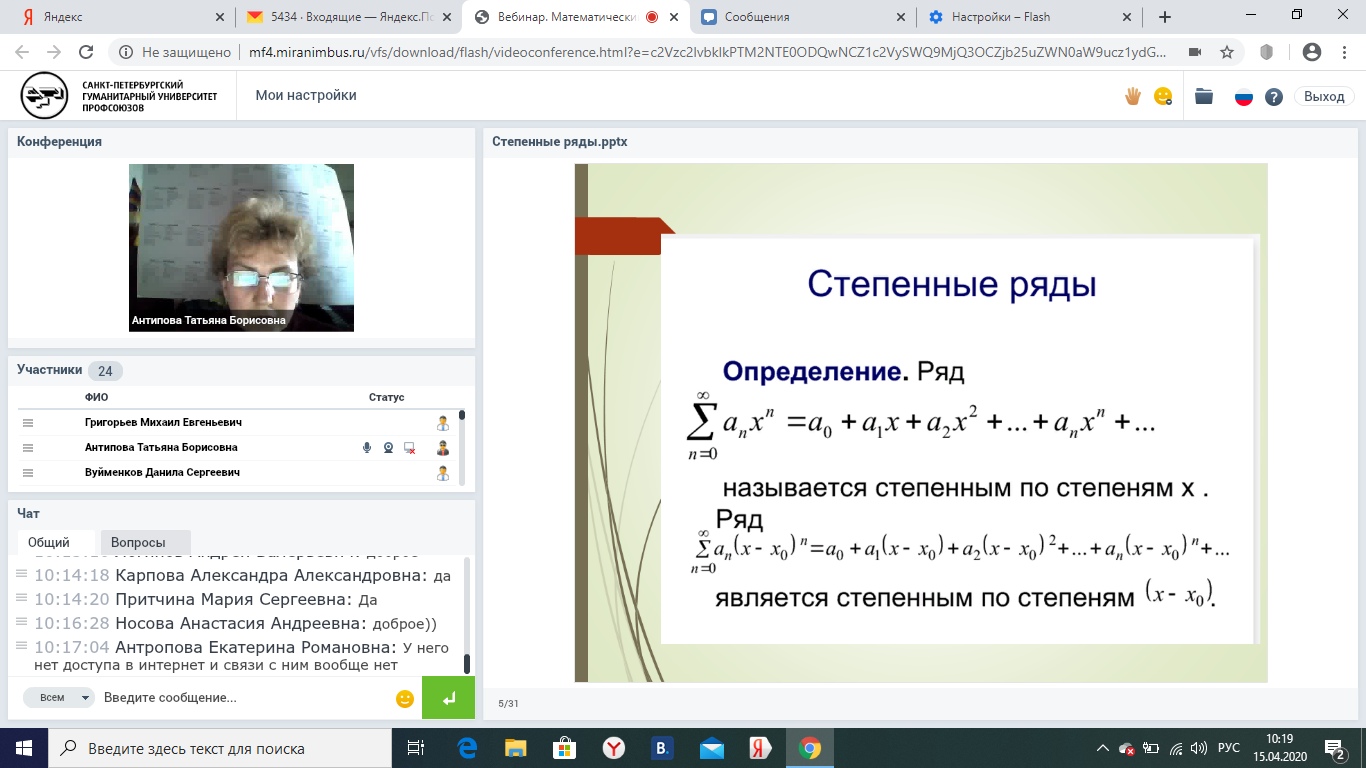
Где – коэффициенты степенного ряда.

Свойства степенных рядов. Непрерывность суммы ряда

1. Сума степенн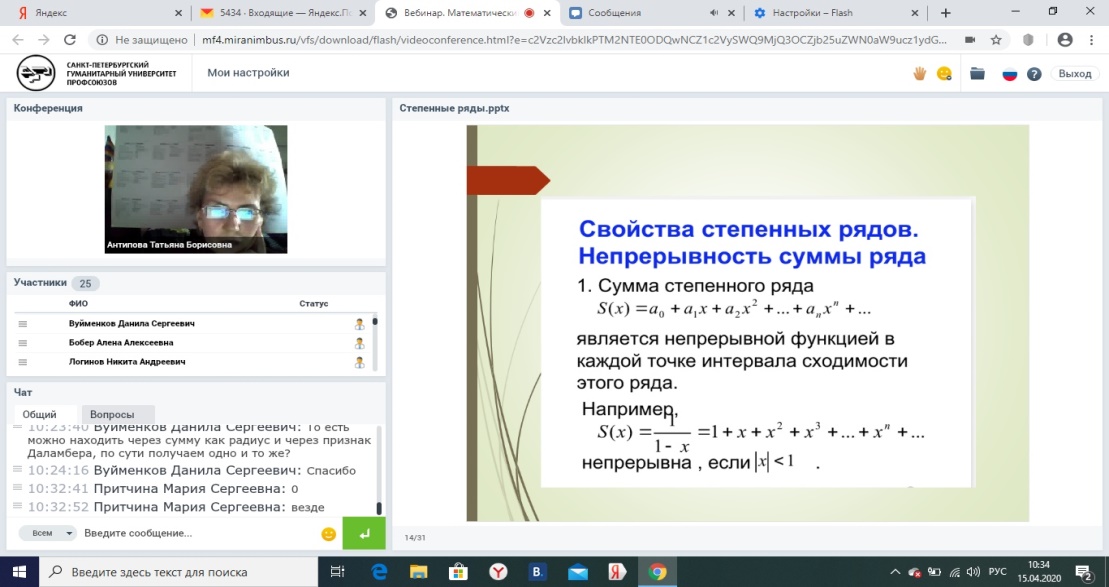ого ряда является непрерывной функцией в каждой точке интервала сходимости того ряда.

Например, непрерывна, если .

2. Почленное дифференцирование. Ряд, полученный почленным дифференцированием степенного ряда, является степенным интервалом с тем же интервалом сходимости, что и данный ряд, причем:

Если

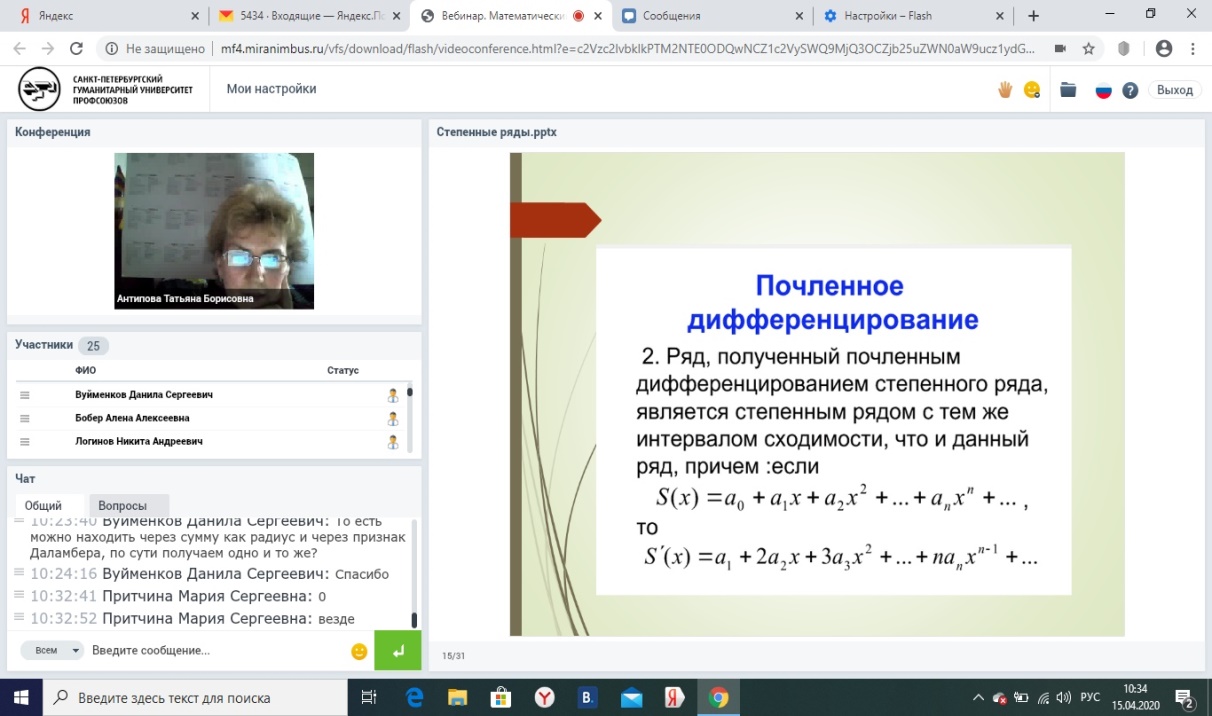
3. Почленное интегрирование. Степенной ряд можно почленно интегрировать на любом промежутке, целиком входящем в интервал сходимости степенного ряда, при этом

Теорема Абеля

• Если степенной ряд сходится при некотором значении x = x₀, отличном от нуля, то он сходится, и притом абсолютно, при всех значениях |x| < |x₀|.

• Следствие. Если степенной ряд расходится при некотором значении x = x₁, то он расходится и при всех значениях |x| > |x₁|.

Замечание. У некоторых рядов интервал сходимости вырождается в точку (R = 0), у других охватывает всю ось Ox (R = ∞).