6. Достаточные признаки сходимости (признак сравнения, признак Даламбера).
Признак сравнения
пусть даны
два ряда
и
с положительными членами, причем члены
первого ряда не превосходят членов
второго, т.е. при любом n
≤
,
тогда:
а) если сходится, то сходится и ;
б) если расходится , то расходится и .
Для сравнения используют ряды:
если α>1 – сходится (например )
если α
1
– расходится (например
)
|q|<1 – ряд сходится
(Это ряд геометрической прогрессии)
Пример№1. Доказать сходимость ряда
-
так как
– сход.
– сход
Признак Даламбера
Пусть для ряда с положительными членами существует предел
D
=
Тогда:
если D < 1 – ряд сходится;
если D > 1 – ряд расходится;
если D = 1 –признак не применяется
Признак Даламбера работает хорошо, когда есть степени и факториалы !!
Пример№2.
-
=
=
Следовательно ряд расходящийся по признаку Даламбера.
7. Достаточные признаки сходимости ( предельный признак сравнения, признак Коши).
Предельный признак сравнения
Если
существует конечный и отличный от нуля
предел
= A, то оба ряда
и
–
одновременно сходятся или расходятся.
Пример№1.
, рассмотрим эталонный ряд
– расход.
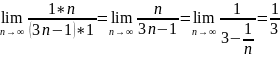
A
,
сл-но
Радикальный признак Коши
Если для ряда существует предел, равный k (с корнем n-ной степени от ), то при
k < 1 – ряд сходится,
k > 1 – ряд расходится,
k = 1 – не идет.
]
ꓱ
= k
Пример№2.
, рассмотрим
K<1,
сл-но
8. Достаточные признаки сходимости (интегральный признак).
Интегральный признак сходимости
Пусть дан ряд
,
члены которого положительны и не
возрастают, т.е.
>0,
>
,
а функция f(x), определенная при х≥1,
непрерывна и не возрастает и f(1)=
;
f(2)=
,…
f(n)=
, тогда для сходимости ряда
необходимо и достаточно, чтобы сходился
интеграл:
Пример№1.
1)
,так как
2) f(x)=
определена и непрерывна при x
3)
Следовательно
-
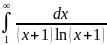расх. И сл-но, по интегральному признаку
сравнения расходится и
9. Знакочередующиеся ряды. Теорема Лейбница.
Под знакочередующимся рядом понимается ряд, члены которого попеременно то больше 0, то меньше 0:
-
+
-
+...+
+…= где
>0.
Данный ряд называется знакочередующимся, т.к. знаки его членов чередуются.
Признак Лейбница (теорема)
Если члены
знакочередующегося ряда убывают по
абсолютной величине|
|>|
|>….>|
|
и предел n-ого члена равен
0 (
=0), то ряд сходится, а его сумма не
превосходит первого члена (S ≤
).
Следствие:
Погрешность
при приближенном вычислении суммы
сходящегося знакочередующегося ряда,
удовлетворяющего условиям теоремы
Лейбница, по абсолютной величине не
превышает абсолютной величины первого
отброшенного члена т.е. |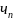
|≤
|
|
( - погрешность, - 1-ый отброшенный член)
Пример№1.
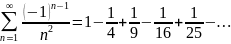
1) знакочер.
2)
убывает, т.к.
3)
Сл-но
-
сх., по теореме Лейбница.
10. Знакопеременные ряды: определение, достаточный признак сходимости
Знакопеременный ряд (u1, u2, …, un) – это ряд, в котором любой его член может быть как положительным, так и отрицательным.
Достаточный признак сходимости(теорема)
Если ряд, составленный из абсолютных величин членов данного знакопеременного ряда | |>| |>….>| | сходится, то сходится и сам знакопеременный ряд.
Замечание: обратное утверждение неверно ⬆
Пример№1.
1) знакочер.
2)
убывает, т.к.
3)
Следовательно
-
сх., по теореме Лейбница.