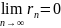- •1. Числовые ряды – основные понятия: определение числового ряда, сходимость и сумма ряда.
- •2. Эталонные ряды: геометрический ряд, гармонический ряд и условия их сходимости.
- •3. Необходимый признак сходимости числового ряда.
- •4. Положительные ряды: определение, достаточные признаки сходимости(перечислить).
- •Признак Даламбера
- •Признак сравнения
- •Предельный признак сравнения
- •Радикальный признак Коши
- •Интегральный признак сходимости
- •5. Свойства сходящихся числовых рядов.
- •6. Достаточные признаки сходимости (признак сравнения, признак Даламбера).
- •7. Достаточные признаки сходимости ( предельный признак сравнения, признак Коши).
- •8. Достаточные признаки сходимости (интегральный признак).
- •9. Знакочередующиеся ряды. Теорема Лейбница.
- •10. Знакопеременные ряды: определение, достаточный признак сходимости
- •11. Абсолютная и условная сходимость знакопеременного ряда
- •12. Свойства абсолютно и условно сходящихся рядов: теорема Коши, теорема Римана
- •13. Функциональный ряд, его точка и область сходимости.
- •14. Степенной ряд. Теорема Абеля и следствие из нее.
- •15. Интервал и радиус сходимости степенного ряда. Определение, формулы для вычисления.
- •16. Разложение функции в степенной ряд
- •17. Ряды Тейлора и Маклорена. Достаточное условие разложения функции в степенной ряд
- •18. Разложение элементарных функций в степенной ряд
- •19. Использование степенных рядов для приближенных вычислений
- •20. Тригонометрический ряд: определение, основные свойства.
- •26. Свойства двойного интеграла.
- •27. Сведение двойного интеграла к повторному. Замена переменных в двойном интеграле.
- •28. Понятие о тройных интегралах.
- •29. Геометрические и механические приложения тройных интегралов.
- •30. Замена переменных в тройных интегралах
- •31. Криволинейные интегралы (понятие, привести пример).
- •32. Криволинейные интегралы I рода
- •33. Вычисление площади фигуры, ограниченной замкнутым контуром.
1. Числовые ряды – основные понятия: определение числового ряда, сходимость и сумма ряда.
Числовой
ряд – бесконечная последовательность
чисел u1;u2;…un;…,
соединённых знаком сложения u1+u2+u3+…+un+…=
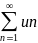
ui-члены ряда, un-общий член ряда (n-ный)
S=

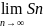
u1+u2+u3+…+un+…=
 S1=u1
S1=u1
Частичные суммы
S3=u1+u2+u3
Sn=u1+u2+..+un
S-сумма ряда
Ряд расходящийся, если предел частичных сумм не существует (например, равен бесконечности). У расходящегося ряда сумма не определена.

2. Эталонные ряды: геометрический ряд, гармонический ряд и условия их сходимости.
Эталонный ряд - это ряд, сходимость которого нам известна.

3. Необходимый признак сходимости числового ряда.
Если ряд сходится,
то предел его общего члена un при n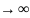 равен нулю, т.е.
равен нулю, т.е.
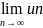 =0.
=0.
Следствие: Если предел у un не равен нулю, то ряд расходится.
.
 0,
то
0,
то
 расход.
расход.
Пример: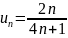

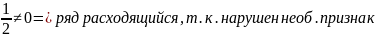
Замечание: Данная теорема выражает необходимый, но не достаточный признак сходимости: если =0, n , то из этого не следует, что ряд сходится.
4. Положительные ряды: определение, достаточные признаки сходимости(перечислить).
Положительные
ряды – ряды, все члены которых
неотрицательны. У такого ряда
последовательность (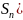 его
частных сумм является возрастающей и,
поэтому для его сходимости достаточно,
чтобы последовательность (
была
ограниченной.
его
частных сумм является возрастающей и,
поэтому для его сходимости достаточно,
чтобы последовательность (
была
ограниченной.
Достаточные признаки сходимости:
Признак Даламбера
Пусть для ряда un с положительными членами (от n=1 до бесконечности) существует предел
Д=

Тогда если Д<1 – ряд сходится;
Д>1 – ряд расходится;
Д=1 –признак не применяется
Признак Даламбера работает хорошо, когда есть степени и факториалы !!
Признак сравнения
пусть даны
два ряда с положительными членами
(ряд 1)
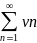 (ряд 2)
(ряд 2)
причем члены первого ряда не превосходят членов второго, т.е. при любом n un ≤ vn,
тогда: а) если сходится ряд 2, то сходится и ряд 1;
б) если расходится ряд 1, то расходится и ряд 2.
Для сравнения используют ряды:
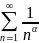 если α>1 – сходится (например
если α>1 – сходится (например
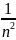
 )
)
если α≤1
– расходится (например

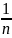 )
)
 |q|<1 – ряд сходится
|q|<1 – ряд сходится
Предельный признак сравнения
Если
И
– ряды с положительными членами и
существует конечный предел отношения
их общих членов(не равных 0) К=
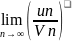 ≠
0 ,то ряды одновременно сходятся, либо
расходятся. Должен быть конечный предел.
≠
0 ,то ряды одновременно сходятся, либо
расходятся. Должен быть конечный предел.
Радикальный признак Коши
Если для
ряда un существует предел
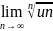 = K,
= K,
то при K<1 – ряд сходится,
K>1 – ряд расходится,
K=1 – не идет.
Интегральный признак сходимости
Пусть дан ряд , члены которого положительны и не возрастают, т.е un >un+1 , а функция f(x), определенная при х≥1, непрерывная и невозрастает.
Полагаем
что f(1)=u1, F(2)=u2, …f(n)=un,… тогда для сходимости
ряда ряд
необходимо и достаточно, чтобы сходился
несобственный интеграл:
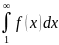 .
.
5. Свойства сходящихся числовых рядов.
1. Если ряд u1+u2+…un+… сходится и имеет сумму S, то и ряд λu1+λu2+…λun+… (полученный умножением данного ряда на число λ (лямбда)) также сходится и имеет сумму λS.
2. Если ряды u1+u2+…un+… и v1+v2+…vn+… сходятся и их суммы равны соответственно S1 и S2, то и ряд (u1+v1)+(u2+v2)+..(представляющий сумму данных рядов) также сходится, и его сумма равна S1+S2.
Свойства 1 и 2 вытекают из свойств пределов числовых последовательностей
3. Если ряд сходится, то сходится и ряд, полученный из данного путем отбрасывания (или приписывания) конечного числа членов.
4. Для того
чтобы ряд сходился, необходимо и
достаточно, чтобы при n→∞
остаток ряда стремился к 0 т.е. чтобы