
Лабораторные / UP_Nelineynye_sistemy_upravlenia
.pdf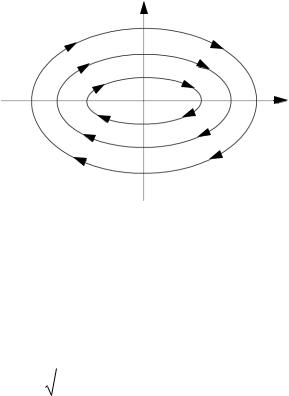
Тогда согласно (2.21) незатухающее движение, являющееся решением (2.15), описывается следующим образом:
x x0 cos 0t ,
y x0 0 sin 0t .
В общем случае при y0 0 система (2.22) имеет вид:
x |
y0 |
sin t x |
cos t , |
||||
|
|||||||
|
0 |
0 |
0 |
|
|
0 |
|
|
|
|
|
|
|
||
y x |
sin |
t y |
0 |
cos t . |
|||
|
0 |
0 |
0 |
|
0 |
||
Преобразуем систему (2.22) к следующему виду:
x |
|
cos t , |
||
|
|
|
||
|
|
0 |
||
x0 |
|
|||
|
y |
sin 0t . |
||
|
|
|||
|
|
|
||
|
|
|
||
|
|
|
|
|
x0 0 |
|
|||
(2.22)
(2.23)
Оба уравнения (2.23) необходимо возвести в квадрат, после чего произвести сложение и воспользоваться основным тригонометрическим тождеством. Тогда снова получим уравнение
эллипса (2.20). |
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
||
Вид фазовых траекторий с особой |
|
|
|
|
|
||||
точкой |
типа |
«центр» |
приведен на |
|
|
|
|
|
|
рис. 2.4. |
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
2. |
Далее |
рассмотрим |
поведение |
|
|
|
|
|
|
систем с вязким трением, т. е. когда |
|
|
|
|
|
||||
h 0 , на примере колебательного звена |
|
|
|
|
|
||||
второго порядка 2 h2 |
. Составим ха- |
|
Рис. 2.4. Фазовые траектории |
||||||
|
|
0 |
|
|
|
||||
рактеристическое уравнение для диф- |
|
с особой точкой типа «центр» |
|||||||
ференциального уравнения (2.14): |
|
|
|
|
|
||||
|
|
|
|
p2 2hp 2 |
0 . |
(2.24) |
|||
|
|
|
|
0 |
|
|
|
|
|
При условии 2 h2 |
решением характеристического уравнения (2.24) |
||||||||
|
|
0 |
|
|
|
|
|
|
|
будет комплексно-сопряженная пара вида |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
p |
|
h j , где |
|
2 h2 . |
(2.25) |
||
|
|
1,2 |
|
|
0 |
|
|
||
21

Если принять дополнительное условие, что h 0 , то вещественная часть пары (2.25) будет отрицательной. При таких корнях характеристического уравнения (2.24) и начальных условиях y0 y 0 , x0 x 0 получим:
x t y0 hx0 e ht sin t x0e ht cos t .
Чтобы изучить характер траекторий, будем исследовать систему при начальном положении изображающей точки на оси абсцисс, т. е. y0 0 :
|
x t x |
|
|
e ht |
|
0 |
|
|
|
|
|
|
|
|
y t x e ht |
||
|
|
0 |
|
|
|
h |
|
|
|
|
|
|
|
|
|
sin t e ht cos t , |
|
||
|
|
|||||
|
|
|
|
|||
|
h |
2 |
|
(2.26) |
||
|
||||||
|
|
sin t. |
|
|||
|
2 |
|
||||
|
|
|
|
|
|
|
|
|
|
|
|||
Из (2.26) следует, что движение фазовых координат происходит по гармоническому закону. При этом может быть показано, например, что амплитуда колебаний координаты x t убывает по экспоненциальной зависимости, которую можно определить следующим образом:
A t e ht |
|
|
|
|
|
y |
hx |
2 x2 . |
(2.27) |
||
x |
0 |
0 |
0 |
|
|
Фазовые траектории представляют собой скручивающиеся к началу координат спирали. Начало координат является особой точкой типа «фокус»:
|
|
любая траектория с течением времени при- |
||
y |
ближается к ней сколь угодно близко, но |
|||
|
|
угол вхождения траектории в фокус уста- |
||
|
|
новить невозможно, поскольку производная |
||
|
|
dy dx в начале координат не существует. |
||
x |
||||
|
|
Итак, фазовые траектории будут иметь |
||
|
|
вид, приведенный на рис. 2.5. При этом |
||
Рис. 2.5. Фазовые траектории |
начало координат носит |
название |
особой |
|
точки типа «устойчивый фокус». |
|
|||
с особой точкой |
|
|||
типа «устойчивый фокус» |
Если рассматривать |
случай, |
когда |
|
h 0, то фокус будет неустойчивым, и траектории будут от него беспредельно отдаляться. Движение представляет собой колебания с нарастающей амплитудой. Приведем фазовые траектории на рис. 2.6. Начало координат носит название особой точки типа «неустойчивый фокус».
22

3. Рассмотрим систему с вязким трением на примере апериодического звена второго порядка h2 02 . Тогда корни характеристического уравнения (2.24) являются вещественными. Если дополнительно задать h 0 , то они, кроме того, будут отрицательными:
p |
h |
h2 2 |
0, где |
p R . |
(2.28) |
1,2 |
|
0 |
|
1,2 |
|
В этом случае в фазовой плоскости существуют две прямолинейные фазовые траектории, проходящие через начало координат, с угловыми коэффициентами, равными значениям корней. Остальные траектории имеют вид параболических кривых, приближающихся к началу координат и входящих в него под углами arctg min pi . Вид же самих фазовых траекторий можно записать так:
 y
y
x
Рис. 2.6. Фазовые траектории с особой точкой
типа «неустойчивый фокус»
x t c e p1t c e p2t , |
|
|
|||
|
1 |
|
2 |
|
(2.29) |
|
|
p1t |
|
p2t |
|
|
|
c2 p2e |
. |
||
y t c1 p1e |
|
|
|||
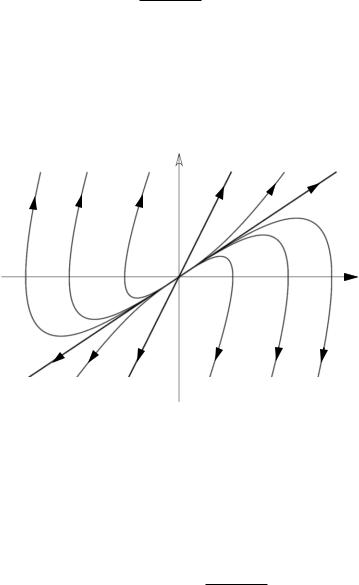
Переходный процесс во временной области в зависимости от начальных значений носит либо монотонный, либо апериодический характер. На рис. 2.7 приведем фазовый портрет, определяемый системой (2.29). При этом начало координат носит название особой точки типа «устойчивый узел».
 y
y
x
Рис. 2.7. Фазовые траектории с особой точкой типа «устойчивый узел»
При этом две прямолинейные фазовые траектории разделяют фазовую плоскость на две области: область с монотонным характером переходных
23
процессов, которая содержит фазовые траектории, не пересекающие ось абсцисс; область с апериодическим характером переходных процессов, которая содержит фазовые траектории, однократно пересекающие ось абсцисс.
Если рассматривать тот же случай, но при условии h 0 , то корни характеристического уравнения будут вещественными и положительными:
p1,2 h 
 h2 02 0 , где p1,2 R .
h2 02 0 , где p1,2 R .
Такие корни соответствуют неустойчивым решениям, которые, как и ранее, описываются системой (2.27). Центр в данном случае называется особой точкой типа «неустойчивый узел». Фазовые траектории приведены на рис. 2.8.
 y
y
x
Рис. 2.8. Фазовые траектории с особой точкой типа «неустойчивый узел»
4. Последний рассматриваемый случай соответствует действию отрицательной позиционной силы. Тогда уравнение (2.14) преобразуется к виду
x hx 2 x 0 . |
(2.30) |
0 |
|
При этом корни характеристического уравнения, соответствующего (2.30), будут иметь вид, аналогичный (2.28):
p1,2 h 
 h2 02 .
h2 02 .
Корни p1,2 будут всегда действительными, но с разными знаками. Нача-
ло координат будет представлять собой особую точку типа «седло», соответствующую неустойчивому состоянию равновесия. Фазовые траектории данной системы приведены на рис. 2.9.
24

 y
y
x
Рис. 2.9. Фазовые траектории с особой точкой типа «седло»
В этом случае, как и в случае положительной позиционной силы, фазовая плоскость разделена двумя прямолинейными фазовыми траекториями с углами наклона, соответствующими значениям корней характеристического уравнения. Однако одна из этих траекторий, имеющая отрицательный угловой коэффициент, устойчивая, а другая – нет.
2.2.4. Фазовые траектории нелинейных систем
Рассмотрим систему с сухим, или кулоновским, трением. Пусть теперь в системе (2.16) действует постоянная по величине сила трения f тр , направ-
ленная навстречу движению. Для удобства выразим эту силу в виде произве-
дения 02 на некоторое положительное число :
|
2 |
dx |
|
|
|
, |
|
|
|
0, |
|
|
|||||
|
0 |
dt |
|
|
|
|
|
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
|
|
fтр 0, |
|
|
|
0, |
|
dt |
|
||||
|
|
|
|
|
|
|
|
dx |
|
|
|
02 , |
|
|
|
0. |
|
dt |
|
|
|||
|
|
|
|
|
|
Когда система движется, динамическая сила, создающая ускорение x , и
сила пружины 02 x уравновешиваются силой трения:
|
x 2 x f |
тр |
, x |
0 . |
(2.31) |
|||||
|
0 |
|
|
|
|
|
|
|
|
|
Это наблюдается, когда |
2 x f |
тр |
или |
|
x |
|
, |
причем избыток силы |
||
|
|
|||||||||
|
0 |
|
|
|
|
|
|
|
|
|
02 x fтр расходуется на создание ускорения. Если же усилие, развиваемое
25

пружиной, меньше силы трения, то система не сможет сдвинуться с места. Таким образом, движение на разных стадиях описывается различными дифференциальными уравнениями:
|
|
2 |
|
dx |
|
|
|
|
|
|
||
|
|
0 |
, |
|
|
|
0, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
dt |
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
x 2 x |
0, |
|
dx |
0, |
|
x |
|
, |
(2.32) |
|||
|
|
|
||||||||||
|
|
|
||||||||||
0 |
|
|
|
dt |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
dx |
|
|
|
|
|
|
|
|
02 , |
|
|
|
0. |
|
|
|
|
|
||
|
|
dt |
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
||
Уравнение (2.32) с правой частью при dx dt 0 определяет траекторию в нижней полуплоскости; правая часть при dx
dt 0 определяет траекторию в нижней полуплоскости; правая часть при dx dt 0 определяет фазовую траекторию в верхней полуплоскости; правая часть при dx
dt 0 определяет фазовую траекторию в верхней полуплоскости; правая часть при dx dt 0, x соответствует отрезку покоя на действительной оси. Этот отрезок является геометрическим местом бесчисленного множества возможных точек равновесия.
dt 0, x соответствует отрезку покоя на действительной оси. Этот отрезок является геометрическим местом бесчисленного множества возможных точек равновесия.
В верхней полуплоскости движение определяется уравнением
x 02 x x '' 02 x 0, x 0 .
Уравнение (2.31) представляет собой уравнение эллипса, центр которого смещен в точку –ε на оси x. Соответственно в нижней полуплоскости:
x 02 x x '' 02 x 0, x 0 ,
получается семейство эллипсов с центром в точке +ε на оси x.
Смещение эллипсов приводит к тому, что изображающая точка, пересекая ось абсцисс, переходит на эллипс меньшего размера и, в конце концов, приходит на отрезок покоя. Так как к любой точке отрезка покоя фазовые траектории подходят сверху и снизу, изображающая точка, попав на отрезок покоя, остается на нем. Следовательно, отрезок покоя устойчив. На рис. 2.10 приведем фазовые траектории для данной системы.
Уравнения движения, получаемые в результате решения дифференци-
альных уравнений (2.32), при начальных условиях y0 0 |
и x0 x 0 имеют |
|||
следующий вид: |
|
|
|
|
а) первый полуэллипс в нижней полуплоскости |
|
|
|
|
x x |
cos t , 0 t |
|
; |
(2.33) |
|
||||
0 |
0 |
0 |
|
|
|
|
|
||
|
26 |
|
|
|

б) первый полуэллипс в верхней полуплоскости
|
|
|
|
|
|
|
|
2 |
|
|
x x |
3 cos |
|
t |
, |
t |
; |
||||
|
|
|
||||||||
0 |
|
0 |
|
0 |
|
0 |
|
0 |
||
|
|
|
|
|
|
|||||
в) второй полуэллипс в нижней полуплоскости
|
|
|
|
2 |
|
2 |
|
3 |
|
x x |
5 cos |
|
t |
, |
t |
||||
|
|
|
|||||||
0 |
|
0 |
|
|
|
0 |
0 |
||
|
|
|
|
0 |
|||||
и т. д.
 y
y
–ε |
ε |
x |
(2.34)
(2.35)
Рис. 2.10. Фазовые траектории нелинейной системы с сухим трением
Анализ выражений (2.33)–(2.35) позволяет говорить о том, что амплитуды последовательных колебаний убывают по линейному закону, и это качественно отличает характер затухания колебаний в нелинейной системе с сухим трением от экспоненциального затухания в линейной системе. Время затухания в линейной системе бесконечно, в рассматриваемой нелинейной – конечно.
2.3. Методика исследования нелинейных систем на фазовой плоскости
2.3.1. Исследование динамики системы при малых отклонениях от положения равновесия
Как известно, фазовые траектории могут содержать особые точки, называемые точками равновесного состояния, когда в математической модели
dxdt1 f1(x1, x2 ),
dx2 f2 (x1, x2 ) dt
27
одновременно выполнены равенства f1(x1, x2 ) 0 и f2 (x1, x2 ) 0 . Поведение системы при малых отклонениях от равновесного состояния с достаточной степенью точности может быть описано линейными дифференциальными уравнениями. Это доказано А. М. Ляпуновым для решения задач устойчивости. При этом поведение необходимо оценивать для всех особых точек, а их может быть достаточно много. Вопросы анализа линейных систем известны и в данном пособии не рассматриваются. Как известно, поведение линейных систем полностью описывается корнями характеристического уравнения. Фазовые траектории для этого случая рассмотрены выше.
2.3.2. Исследование динамики систем при больших отклонениях от положения равновесия
После определения особых точек и оценки динамических режимов «в малом» необходимо решить задачу, которую можно сформулировать так:
определить наличие других установившихся процессов, кроме равновесных;
при наличии таких процессов определить, каковы условия, обеспечивающие неизменность работы системы в каждом из этих режимов.
Первый из вопросов проясняется путем определения наличия периодических колебательных режимов, которым на фазовой траектории соответствуют особые устойчивые замкнутые траектории – устойчивые предельные циклы.
Для решения второго вопроса нужно выделить также области значений координат изображающей точки, в каждой из которых с течением времени достигается лишь один из возможных установившихся режимов работы. Эти области называются областями притяжения этих режимов и образуются они особыми неустойчивыми траекториями – неустойчивыми предельными циклами и сепаратрисами седел (сепаратриса – асимптота, по которой изображающая точка уходит в бесконечность).
Все это накладывает серьезные трудности на анализ и синтез нелинейных систем. Относительно точные результаты можно получить для автоколебательных и кусочно-линейных систем.
2.3.3. Метод точечных преобразований
При определении периодических режимов и особенно при точном исследовании устойчивости этих режимов и границ областей их притяжения
28

можно использовать один из методов исследования нелинейных систем – метод точечных преобразований.
Рассмотрим идею метода точечного преобразования. Для этого запишем в общем виде уравнения динамики нелинейной системы второго порядка без внешнего воздействия:
dx |
F x, y , |
dy |
F |
x, y . |
(2.36) |
|
|
||||
dt |
1 |
dt |
2 |
|
|
|
|
|
|
||
На фазовой плоскости x, y построим три возможных варианта фазовых траекторий, соответствующих (2.36), и линию AB, которая пересекает фазовые траектории под одним и тем же углом (рис. 2.11).
y 
M
M B
M ц
A |
x |
0
Рис. 2.11. Метод точечных преобразований
Пусть решение уравнений системы (2.36) x x t , y y t дает фазовую траекторию, проходящую через точку М. Допустим далее, что с увеличением времени t эта фазовая траектория снова пересечет отрезок AB в некоторой другой точке M .
Точка M (первого пересечения отрезка AB той же фазовой траекторией)
называется последующей по отношению к исходной точке М. |
|
Зависимость |
|
M T M , |
(2.37) |
соответствующая фазовой траектории в силу решения уравнений системы
(2.36), называется функцией последования или точечным преобразованием.
29
Функция последования определяет закон точечного преобразования для данной нелинейной функции.
Определение последующих точек по заданным исходным на отрезке AB
и называется точечным преобразованием отрезка AB самого в себя. Ввиду непрерывности расположения фазовых траекторий исходные и последующие точки заполняют весь отрезок. Однако каждая точка AB необязательно имеет последующую внутри этого отрезка. Фазовые траектории, пересекающие от-
резок, могут и не возвращаться к нему. |
|
Возможен такой случай, когда последующая точка M |
совпадает с ис- |
ходной М, т. е. |
|
Mц T Mц . |
(2.38) |
При этом получается замкнутая фазовая траектория: предельный цикл или кривая, соответствующая особой точке типа «центр». Последнее выясняется из хода соседних фазовых траекторий. Случай (2.38) называется точеч-
ным преобразованием точки M самой в себя. Это неподвижная точка в об-
щем точечном преобразовании отрезка AB.
Если обозначить через s координату произвольной точки M на отрезке AB, отсчитывая длину отрезка вдоль AB от начала A, а координату последующей точки M по отрезку AB обозначить s , то можно изобразить графически функцию последования s f s (рис. 2.12). Проведем из начала координат наклонную прямую под углом 45 (биссектрису координатного угла). Если она пересечется с кривой f s , то точка пересечения даст координату sц замкнутой фазовой траектории.
Ход точечного преобразования прослеживается на этом графике следующим образом. Возьмем исходную точку s0 правее точки sц . Точке s0 соответствует определенное значение s (точка N) на кривой f s . Таким образом, мы нашли координату последующей точки. Теперь примем ее за новую исходную точку. Для этого достаточно провести отрезок NM, параллельный оси абсцисс, из полученной точки N до биссектрисы координатного угла. Проведя далее из точки M вертикаль ML, найдем значение координаты s новой последующей точки и т. д. Из этого простого построения видно, что процесс в данном случае сходится к предельному циклу sц .
30
