
MathCad_4-5
.pdf
Міністерство транспорту та зв’язку України Дніпропетровський національний університет залізничного транспорту імені акад. В.Лазаряна
Львівська філія
ІНТЕГРОВАНА МАТЕМАТИЧНА СИСТЕМА
MathCAD 2000
ч. 4-5
“ТАБУЛЮВАННЯ ТА ПОБУДОВА ГРАФІКІВ ФУНКЦІЙ. РОЗВ'ЯЗУВАННЯ РІВНЯННЬ З ОДНИМ НЕВІДОМИМ.”
Інструкція до лабораторної роботи з курсу “Обчислювальна техніка та програмування”
Львів 2002
Лабораторна робота № 4 - 5.
Тема: Табулювання та побудова графіків функцій. Розв'язування рівняннь з одним невідомим.
Мета: Навчитись користуватись палітрами математичних операцій та відповідними командами меню в середовищі MathCAD.
1. Табулювання функцій і побудова графіків.
Побудувати таблицю значень функції можна двома способами: 1.1. Задати інтервал зміни аргументу у форматі
x:=початкове значення[,початкове значення+крок]..кінцеве значення
в дужках вказаний необов'язковий параметр, якщо його немає, то крок по замовчуванню рівний 1.
Потім можна визначити функцію від цього аргумента, наприклад:
x := 0,0.1.. |
π |
|
f(x) := x cos (3 x)2 |
Двокрапка ".." вводиться символом крапка з комою ";" |
||
|
|
|
2 |
|
|
або кнопкою арифметичної палітри |
x = |
|
f(x) = |
|
Введіть x= |
і отримаєте таблицю значень змінної x. Щоб вивести |
|
|
|
|
|
|
||
0 |
|
|
|
0 |
||
|
|
|
таблицю значень функції введіть f(x)=. Так можна отримати перші 50 |
|||
0.10.091 значень змінної чи функції.
|
|
|
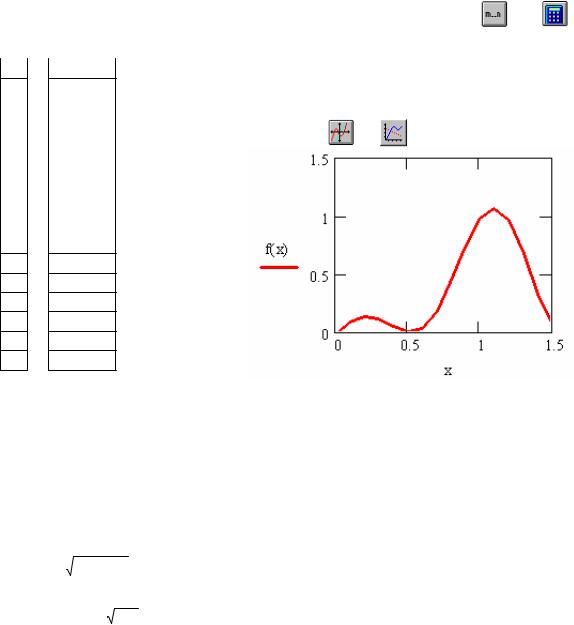
Тепер можна побудувати графік. Розкриємо графічну палітру і |
|
0.2 |
0.136 |
|||
виберемо на ній x-y графік. |
||||
|
|
|
||
0.3 |
0.116 |
|||
|
||||
|
|
|
|
|
0.4 |
0.053 |
|
||
|
|
|
|
|
0.5 |
|
2.502·10 -3 |
|
|
0.6 |
0.031 |
|
||
|
|
|
|
|
0.7 |
0.178 |
|
||
|
|
|
|
|
0.8 |
0.435 |
|
||
|
|
|
|
|
0.9 |
0.736 |
|
||
10.98
1.11.073
1.20.965
1.30.685
1.40.336
1.50.067
Впозиції маркера осі х вкажемо змінну х, в позиції маркера осі y вкажемо функцію f(x). Більше можно нічого не вводити, просто клацнути мишею поза графіком.
Можна також явно вказати границі зміни змінної і функції.
Подвійне клацання мишею на графіку викликає меню настройки, яке дозволяє змінити багато характеристик графіка. Одночасно на графіку можна відобразити до 16 кривих з спільним аргументом. Для цього треба вказати через кому список функцій. Аргументи також можна вказувати через кому.
Побудуйте самостійно на одному малюнку графіки функцій
u(x) := x sin(x)
v(x) := 1 + sin(x)2 w(x) := e−x2
z(x) := log(1 + x − 1)
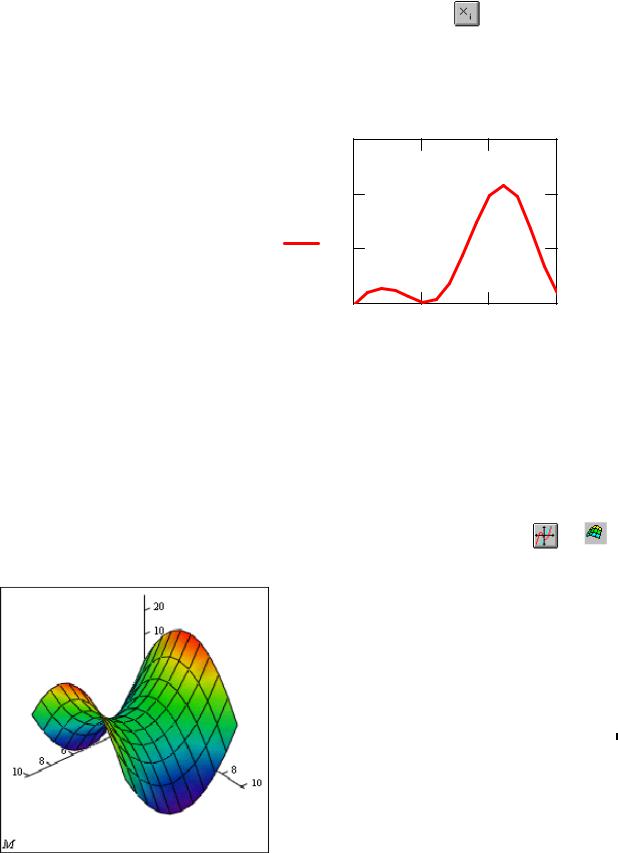
1.2. Визначити змінну цілого індекса і побудувати таблицю значень функцій в вигляді вектор-стовбця. Зокрема для попередньої задачі:
i := 0..15 |
xi := |
i |
|
yi := xi cos (3 xi)2 |
|
10 |
|||||
|
|
|
|||
|
|
0 |
|
|
0 |
|
0 |
0 |
|
0 |
0 |
|
1 |
0.1 |
|
1 |
0.091 |
|
2 |
0.2 |
|
2 |
0.136 |
|
3 |
0.3 |
|
3 |
0.116 |
|
4 |
0.4 |
|
4 |
0.053 |
|
5 |
0.5 |
|
5 |
2.502·10 -3 |
|
6 |
0.6 |
|
6 |
0.031 |
x = |
7 |
0.7 |
y = |
7 |
0.178 |
|
8 |
0.8 |
|
8 |
0.435 |
|
9 |
0.9 |
|
9 |
0.736 |
|
10 |
1 |
|
10 |
0.98 |
|
11 |
1.1 |
|
11 |
1.073 |
|
12 |
1.2 |
|
12 |
0.965 |
|
13 |
1.3 |
|
13 |
0.685 |
|
14 |
1.4 |
|
14 |
0.336 |
|
15 |
1.5 |
|
15 |
0.067 |
|
|
|
|
|
|
Змінна з індексом вводиться так: x[i Отримуємо xi
Важливо знати!
В Mathcad прийнято, що індекс масиву відраховується від 0. Початковий індекс визначається системною змінною ORIGIN=0.
1.5 |
|
|
|
1 |
|
|
|
yi |
|
|
|
0.5 |
|
|
|
0 0 |
0.5 |
1 |
1.5 |
|
|
xi |
|
Доступ до елементів масиву проходить за індексом, наприклад: y0 = 0
y1 = 0.091 y2 = 
Вибір способу побудови функції не дуже важливий, однак при обчисленні значення функції як елементу масиву спрощується процедура доступу до його окремих значень.
Для двовимірного масиву вводиться так: M[i,j |
а отримується |
Mi , j |
||
Двовимірний масив відповідає значенню функції двох змінних, наприклад: |
||||
f(x,y) := x2 − y2 |
i := 0..10 |
j := 0..10 |
xi := −5 + i |
y j := −5 + j |
Визначимо двовимірну матрицю: Mi , j := f(xi ,y j) і побудуємо поверхню. Єдиним аргументом графіка вказуємо ім'я матриці М
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
|
|
0 |
0 |
9 |
16 |
21 |
24 |
25 |
24 |
21 |
16 |
9 |
|
|
1 |
-9 |
0 |
7 |
12 |
15 |
16 |
15 |
12 |
7 |
0 |
|
|
2 |
-16 |
-7 |
0 |
5 |
8 |
9 |
8 |
5 |
0 |
-7 |
|
|
3 |
-21 |
-12 |
-5 |
0 |
3 |
4 |
3 |
0 |
-5 |
-12 |
|
M = |
4 |
-24 |
-15 |
-8 |
-3 |
0 |
1 |
0 |
-3 |
-8 |
-15 |
|
|
||||||||||||
|
5 |
-25 |
-16 |
-9 |
-4 |
-1 |
0 |
-1 |
-4 |
-9 |
-16 |
|
|
6 |
-24 |
-15 |
-8 |
-3 |
0 |
1 |
0 |
-3 |
-8 |
-15 |
|
|
7 |
-21 |
-12 |
-5 |
0 |
3 |
4 |
3 |
0 |
-5 |
-12 |
|
|
8 |
-16 |
-7 |
0 |
5 |
8 |
9 |
8 |
5 |
0 |
-7 |
|
|
9 |
-9 |
0 |
7 |
12 |
15 |
16 |
15 |
12 |
7 |
0 |
|
|
10 |
0 |
9 |
16 |
21 |
24 |
25 |
24 |
21 |
16 |
9 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Двічі клацнувши мишею в області графіка можемо викликати меню настройки і вибрати потрібні установки

1.3 .Розглянемо на прикладі кардіоіди побудови полярного графіка. |
|
φ:= 0,0.1..2 π |
ρ(φ):= 1 + cos (φ) |
Для вводу φ, ρ використаємо палітру грецьких символів
ρ(φ)
φ
Побудуйте самостійно в полярних координатах графіки функцій:
1.ρ(φ):= cos (φ) sin(φ)
2.ρ(φ):= φ
3.ρ(φ):= eφ
2. Розвязання алгебраїчних і трансцендентних рівняннь.
2.1. Розвязання рівняннь за допомогою функції root.
В середовищі MathCAD розв'язувати алгебраїчні або трансцендентні рівняння f(x)=0 з одним або кількома невідомими можна різними способами. Один з них - за допомогою внутрішньої функції
(оператора) k:=гооt(f(x),x).
Першим аргументом оператора root є або функція f(x)=<вираз>, визначена де-небудь в робочому документі вище оператора root, або сам вираз. Другий аргумент - ім'я змінної х, варіюючи якою MathCAD намагається обернути вираз на ноль. Цій змінній перед використанням оператора root потрібно присвоїти числове значення. MathCAD використовує це значення як початкове наближення при пошуку кореня k.
Функція root повертає значення k = х, при якому функція f(x) або вираз перетворюється на ноль. Скаляр k є коренем рівняння f[x) = 0.
Задача розв'язування рівняння з одним невідомим виду f(x)=g(x) є еквівалентна до задачі пошуку кореня виразу f(x) - g(x) = 0. В цьому випадку функція root використовується в такому вигляді: root(f(x) - g(x),x).
Перед використанням оператора root треба дослідити графік функції у=f(x) з метою визначення кількості коренів і їхніх проміжків ізоляції. Щоб таке дослідження зробити, треба протабулювати функцію у=f(x) та побудувати її графік.
MathCAD в функції root використовує комбінований метод Ньютона-січних, тому в якості початкового наближення х можна брати числове значення або лівого, або правого проміжка ізоляції кореня. Обидва вони є рівнозначні, але величина цього проміжка впливає на швидкість обчислення: чим меншим буде проміжок ізоляції, тим ближчим до кореня буде його початкове наближення і тим швидше функція root буде збігатись до значення кореня з точністю TOL.
Початкове значення, присвоєне змінній х, є першим наближення до шуканого кореня. Коли значення виразу у=f(x) при черговому наближенні стане менше за значення внутрішньої змінної TOL = 0.001, корінь вважається знайденим і функція root повертає результат а, який є коренем рівняння у=f(x).
Якщо треба змінити точність; з якою функція root відшукує корінь, слід змінити значення внутрішньої змінної TOL. Якщо значення TOL збільшити, то функція root буде збігатись швидше, але відповідь буде менш точною, й навпаки.
Якщо після багатьох ітерацій MathCAD не може здобути наближення з точністю TQL, то з'явиться повідомлення про помилку: "відсутня збіжність”. Ця помилка може бути викликана такими причинами:
-рівняння не має коренів;
-корені рівняння розміщені надто далеко від початкового наближення;
-вираз має локальний максимум або мінімум між початковим наближенням і коренями;
-вираз має розриви між початковим наближенням і коренями;
-вираз має комплексний корінь, а початкове наближення було дійсним (або навпаки).
Щоб встановити причину помилки, треба дослідити графік функції у=f(x) вказаним вище способом. |
||||||||
Щоб визначити кількість коренів, досить побудувати графік функції у=f(x) на інтервалі x є [а; b] й |
||||||||
підрахувати, скільки разів цей графік перетинає вісь абсцис Х. |
|
|
||||||
Щоб точніше визначити проміжки ізоляції коренів, треба протабулювати досліджувану функцію |
||||||||
у=f(x) в n точках. Проміжком ізоляції того чи іншого кореня функції у=f(x) вважаються такі найближчі |
||||||||
числові значення незалежної змінної х, між якими функція у=f(x) змінює свій знак (з " - " на " + "або, |
||||||||
навпаки, з " + " на " - ". В якості початкового наближення х функції root можна брати числове значення |
||||||||
як лівого, так і правого проміжка ізоляції кореня. |
|
|
|
|
||||
Величину інтервалу [а; Ь] і кількість точок табулювання п треба підбирати експериментально, |
||||||||
пам'ятаючи, що кінцевою метою цього дослідження є визначення не лише кількості коренів, а і |
||||||||
величини їхніх проміжків ізоляції. |
|
|
|
|
|
|
|
|
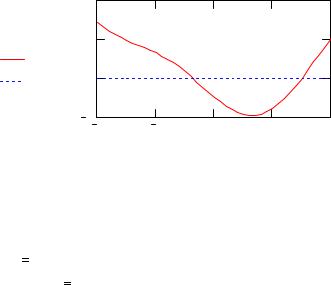
Приклад: Знайти всі корені трансцендентного рівняння |
|
x2 − e0.5 x − sin(2 x) =0 |
|
|||||
|
x := −2.0,−1.9..2.0 |
|
|
f(x) := x2 − e0.5 x − sin(2 x) |
|
|
||
|
|
4 |
|
|
|
|
|
|
|
x2−e0.5 x−sin(2 x) |
2 |
|
|
|
|
|
|
|
0 |
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
2 |
1 |
0 |
1 |
2 |
|
Результат: |
Перше наближення |
|
|
|
x |
Перший корінь |
|
|
|
|
|
|
|
|
|||
|
x := −1 |
|
|
|
x := root(f(x) ,x) |
x = −0.378 |
||
|
Друге наближення |
|
|
|
|
Другий корінь |
|
|
|
x := 1 |
|
|
|
x := root(f(x) ,x) |
x = 1.502 |
||
Знайти корені рівняння f(x)=0 функцією root(f(x),x) |
|
|
|
|||||
x5 + 2 x4 + 3x3 + 4 x2 + 5 x + 6 0 |
|
|
|
|
|
|
|
|
6 x5 + 0.5 x4 + 4 x3 − 31 x2 + 2.5 x + 13 |
0 |
|
|
|
|
|
|
|
2.2. Розвязання рівняннь за допомогою ключового слова Given |
і функції Find. |
|||||||
Приклад: Знайти за допомогою ключового слова Given |
і функції Find всі корені трансцендентного |
|||||||
рівняння попереднього прикладу |
x2 − e0.5 x − sin(2 x) =0. |
|
|
|
||||
Якщо це рівняння записати у вигляді |
|
|
|
|
|
|||
|
f(x)= x2 − e0.5 x − sin(2 x) =0, |
|
|
|
|
|
||
то для визначення кількості коренів і їхніх наближень можна скористатись графіком цієї функції, |
||||||||
зображеним вище. |
|
|
|
|
|
|
|
|
Рівняння x2 − e0.5 x − sin(2 x) =0 можна записати і в іншому вигляді, наприклад в такому: |
||||||||
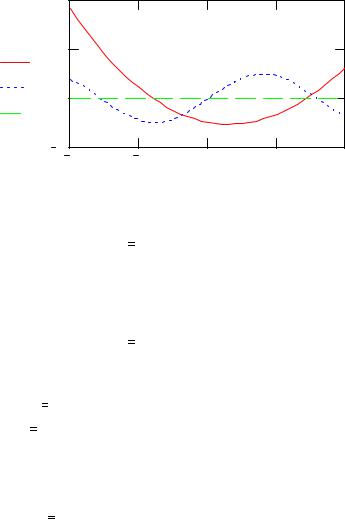
x2 − e0.5 x =sin(2x). Тоді, щоб визначити кількість коренів і їхніпочатковінаближення, треба |
||||||||
побудувати графіки двох функцій - f1(x)= x2 − e0.5 x та f2(x)=sin(2x), які задають ліву і праву частини |
||||||||
досліджуваного рівняння. З рисунка видно, що рівняння x2 − e0.5 x =sin(2x) має два корені k1 i k2, |
||||||||
оскільки графіки функцій f1(х) і f2(x) перетинаються двічі. |
|
|
|
|||||
x := −2.0,−1.9..2.0
|
|
4 |
|
|
|
|
|
x2−e0.5 x |
2 |
|
|
|
|
|
|
sin(2 x) |
|
|
|
|
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
2 |
2 |
1 |
0 |
1 |
2 |
Результат: |
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
Перше наближення |
|
x:=-1 |
|
|
|
|
|
|
|
|
Given |
|
|
|
|
|
|
|
x2 − e0.5 x |
sin(2 x) |
|
|
|
Перший корінь |
|
Find(x)=0.378 |
|
|
|
|
|
Друге наближення |
x:=1 |
Given |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x2 − e0.5 x |
sin(2 x) |
|
|
|
Другий корінь |
|
Find(x)=1.502 |
|
|
|
|
|
Знайти корені рівняння f(x)=0 функцією Find(f(x),x) |
|
|
|||||
7 cos (x) sin(3 x) + 2 x − 0.3 |
|
0 |
|
|
|
|
|
2 sin(5 x) + 1.75 x2 − 0.35 |
0 |
|
|
|
|
|
|
2.3. Знаходження коренів алгебраїчного полінома за допомогою функції polyroots.
Для знаходження коренів алгебраїчного полінома степеня n , який має вигляд
νn xn + .... + νn x2 + ν1 x + ν0 0
де ν0 ν1 νn -коефіцієнти полінома, треба користуватись функцією polyroots
Функція polyroots(v) не потребує початкового наближенняі одночасно повертає всі корені
полінома степеня n (як дійсні, так і комплексні ) у вигляді вектора довжиною n.
Коефіцієнти полінома знаходяться у векторі V=( ν0 ..... νn ) |
довжиною n+1 |
||
Приклад : Знайти всі корені полінома |
x3 − 10 x + 2 |
|
0 |
|
|||
|
|||
|
|
2 |
|
|
|
−3.258 |
|
|
|
−10 |
|
|
|||
v := |
|
|
polyroots (v) = |
|
0.201 |
|
|
|
0 |
|
|
|
|||
|
|
3.057 |
|
||||
|
|
1 |
|
|
|
||
|
|
|
|
|
|
||
Знайти корені рівняння f(x)=0 функцією polyroots x5 + 2 x4 + 3x3 + 4 x2 + 5 x + 6  0
0
6 x5 + 0.5 x4 + 4 x3 − 31 x2 + 2.5 x + 13  0
0
Контрольні запитання
1.Що називається коренем (коренями) рівняння f(x)=0 ?
2.Чим відрізняються алгебраїчні рівняння від трансцендентних ?
3.Що таке проміжки ізоляції коренів та за якими способами їх можна визначити ?
4.Чим відрізняється функція root від функції polyroots? Для якої з них потрібно визначати початкові наближення коренів? Яка з них може обчислювати корені трансцендентних рівнянь ?
5.За допомогою якої функції можна обчислювати комрлексні корені алгебраїчних рівнянь ?
