
Лаб.роб.Excel N3
.pdfЛ А Б О Р А Т О Р Н А Р О Б О Т А № 3
ВИКОРИСТАННЯ ТАБЛИЧНОГО ПРОЦЕСОРА EXCEL ДЛЯ РОЗВ’ЯЗУВАННЯ РІВНЯНЬ
Мета роботи:
1.Опанування методами розв’язування систем лінійних та нелінійних алгебраїчних рівнянь.
2.Набуття практичних навичок роботи з матричними функціями.
3.Опанування методами ітераційного обчислювального процесу.
Перед виконанням лабораторної роботи слід ознайомитися з теоретичним матеріалом, поданим у методичному посібнику [1].
1.ПОРЯДОК ВИКОНАННЯ РОБОТИ
1.1.Отримайте завдання до виконання лабораторної роботи у викладача.
1.2.Ознайомтеся з умовами задачі і методичними вказівками їх вико-
нання.
1.3.Підготуйте проект електронної таблиці на папері з номерами рядків, назвами стовпців, основними формулами, текстовими і числовими даними.
1.4.Визначте основні кроки послідовності оптимального виконання ро-
боти.
1.5.Внесіть та відредагуйте данні у комірках електронної таблиці згідно
зпідготованим заздалегідь її проектом.
1.6.Отримайте результати обчислень.
1.7.Підготуйте електронні таблиці до друку.
1.8.Надрукуйте результати роботи.
1.9.Виконайте звіт до лабораторної роботи та здайте викладачу на пере-
вірку.
1
2. РОЗВ’ЯЗУВАННЯ ЛІНІЙНИХ МАТРИЧНИХ РІВНЯНЬ
Сукупність систем лінійних алгебраїчних рівнянь, які відрізняються лише правими частинами, можна представити у вигляді одного лінійного матричного рівняння
A X = B .
Тут A - квадратна матриця розміру n ×n , В – прямокутна матриця розміру n ×m . Розв’язком рівняння є матриця Х такого ж розміру, як і матриця
В.
Якщо визначник матриці A не дорівнює нулю, то існує обернена до неї матриця A−1 і можна отримати розв’язок матричного рівняння.
Знаходимо обернену матрицю до матриці A і помножимо зліва матричне
рівняння на A−1
A−1A X = A−1B .
Оскільки A−1A = E – одинична матриця, то A−1A X = E X = X , і шукана матриця Х знаходиться за формулою
X = A−1B .
Усі зазначені дії можна виконати використовуючи функції Excel для операцій з матрицями.
Нагадаємо, що визначник матриці повертає функція Excel МОПРЕД, обернену матрицю – функція МОБР, а для множення матриць призначена функція МУМНОЖ.
Більш детальні відомості про матричні функції приведені у розділі 2 посібника [1].
Приклад.
Нехай задані наступні матриці
1 |
3 |
5 |
4 |
6 |
2 |
8 |
||||
|
5 |
2 |
−2 |
2 |
|
|
3 |
5 |
5 |
|
|
|
|
|
|||||||
A = |
3 |
1 |
−2 |
4 |
|
B = |
1 |
6 |
|
. |
|
|
|
−1 |
|||||||
|
2 |
1 |
2 |
2 |
|
|
4 |
3 |
4 |
|
|
|
|
|
|||||||
Побудувати електронну таблицю для обчислення матриці Х, як розв’язку матричного рівняння A X = B .
2
Розв’язування. На робочому аркуші потрібно визначити діапазони комірок, у які внесемо елементи заданих матриць A та В, а також для обчислених оберненої матриці A−1 і матриці Х.
Сплануємо наступне заповнення робочого аркуша (рис. 1).
Таким чином, вхідні дані розмістимо у діапазонах комірок В3:Е6 – матриця A і G3:I6 – матриця В.
|
A |
B |
|
С |
|
D |
E |
F |
|
G |
|
H |
|
I |
J |
1 |
|
Розв |
’язування матричного рівняння АХ=В |
|
|
||||||||||
2 |
|
|
|
Матриця А |
|
|
|
|
Матриця В |
|
|
||||
3 |
|
1 |
3 |
|
5 |
4 |
|
|
6 |
2 |
|
8 |
|
||
4 |
|
5 |
2 |
|
-2 |
2 |
|
|
3 |
5 |
|
5 |
|
||
5 |
|
3 |
1 |
|
-2 |
4 |
|
|
1 |
6 |
|
-1 |
|
||
6 |
|
2 |
1 |
|
2 |
2 |
|
|
4 |
3 |
|
4 |
|
||
7 |
Визначник матриці А: |
|
|
|
|
|
|
|
|
|
|||||
8 |
|
|
|
|
|
|
|
|
|
||||||
9 |
|
Обернена матриця А-1 |
|
|
|
|
|
|
|
|
|||||
10 |
|
|
|
|
|
|
|
|
|
||||||
11 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
|
|
|
|
|
|
|
|
Перевірка розв’язку |
|
|||||
15 |
|
|
|
|
|
|
|
|
|
||||||
16 |
|
|
Матриця Х |
|
|
|
|
Матриця А·Х |
|
||||||
17 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
19 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Рис. 1. Розташування даних у комірках робочого аркуша
Проміжні результати – визначник матриці A у комірці Е8 і обернена матриця A−1 у діапазоні В11:Е14.
Розв’язок задачі отримаємо у діапазоні В17:D20 – матриця Х.
Крім того, виділимо діапазон комірок G17:I20 для добутку матриць A X , тобто для перевірки отриманого розв’язку підстановкою його в рівняння. Значення у комірках цього діапазону повинні збігатися зі значеннями діапазону G3:I6, у якому розміщена матриця В.
3
Відповідно до такої структури таблиці внесемо вхідні дані в комірки, запишемо розрахункові формули та виконаємо такі дії.
1. Обчислимо визначник матриці A.
У комірку Е8 внесемо формулу = МОПРЕД(В3:Е6) для обчислення визначника. Якщо отримане значення не дорівнюватиме нулю, то продовжимо вносити формули в комірки. В іншому випадку роботу завершуємо.
2. Обчислимо обернену матрицюA−1 .
У комірку В11 внесемо формулу = МОБР(В3:Е6), яка обчислить перший елемент оберненої матриці. Після цього виділимо мишею діапазон комірок В11:Е14. Натискаємо клавішу F2, і у комірці висвітлюється внесена у неї формула. На завершення натискаємо комбінацію клавіш Ctrl+Shift+
Enter. У |
кожній |
комірці виділеного діапазону маємо формулу вигляду |
|||
{= МОБР(В3:Е6)}, що дозволить отримати у діапазоні комірок В11:Е14 |
об- |
||||
числені за цими формулами елементи оберненої матриці. |
|
|
|||
3. Знаходимо матрицю Х. |
|
|
|
||
У комірку В17 |
внесемо формулу = МУМНОЖ( В11:Е14 ; G3:I6 ), |
щоб |
|||
отримати |
перший |
елемент |
добуткуA−1B . Виділимо |
діапазон комірок |
|
В17:D20, натискаємо клавішу |
F2 і комбінацію клавіш |
Ctrl+Shift+Enter. У |
|||
діапазоні комірок матимемо формули {= МУМНОЖ( В11:Е14 ; G3:I6 )}, які дають значення елементів матриці Х.
4. Перевіримо отриманий розв’язок підстановкою його у рівняння.
У комірку G17 внесемо формулу = МУМНОЖ( В3:Е6 ; В17:D20 ), щоб обчислити перший елемент масиву добуткуA X . Інші елементи цього добутку отримаємо так, як і у попередньому пункті. Виділимо діапазон комірок G17:I20, натискаємо клавішу F2 і комбінацію клавіш Ctrl+Shift+Enter. У діапазоні комірок матимемо формули {= МУМНОЖ( В3:Е6 ; В17:D20 )}. У разі правильного розв’язання задачі значення у комірках повинні дорівнювати значенням матриці В.
5. Надаємо таблиці вигляду, придатного для звіту про виконання роботи. Змінюємо формати відображення числових значень у комірках та діапа-
зонах комірок таблиці, а також наводимо межі комірок (рис. 2).
6. Друкуємо отримані результати.
Виділяємо діапазон комірок A1:J21 і виконаємо команду Файл | Печать . Поставимо перемикач в позицію Выделеный диапазон і надрукуємо виділений діапазон – ОК.
4
|
A |
B |
С |
D |
E |
F |
|
G |
|
H |
|
I |
J |
1 |
|
Розв |
’язування матричного рівняння АХ=В |
|
|
||||||||
2 |
|
|
Матриця А |
|
|
|
|
Матриця В |
|
|
|||
3 |
|
1 |
3 |
5 |
4 |
|
|
6 |
2 |
|
8 |
|
|
4 |
|
5 |
2 |
-2 |
2 |
|
|
3 |
5 |
|
5 |
|
|
5 |
|
3 |
1 |
-2 |
4 |
|
|
1 |
6 |
|
-1 |
|
|
6 |
|
2 |
1 |
2 |
2 |
|
|
4 |
3 |
|
4 |
|
|
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
8 |
Визначник матриці А: |
100 |
|
|
|
|
|
|
|
|
|||
9 |
|
Обернена матриця А-1 |
|
|
|
|
|
|
|
|
|||
10 |
|
|
|
|
|
|
|
|
|
||||
11 |
|
-0,2 |
0,1 |
-0,1 |
0,5 |
|
|
|
|
|
|
|
|
12 |
|
0,44 |
0,38 |
-0,18 |
-0,9 |
|
|
|
|
|
|
|
|
13 |
|
-0,04 -0,08 -0,12 |
0,4 |
|
|
|
|
|
|
|
|
||
14 |
|
0,02 |
-0,21 |
0,31 0,05 |
|
Перевірка розв’язку |
|
||||||
15 |
|
|
|
|
|
|
|
||||||
16 |
|
Матриця Х |
|
|
|
Матриця А·Х |
|
||||||
17 |
|
1 |
1 |
1 |
|
|
|
6 |
2 |
|
8 |
|
|
18 |
|
0 |
-1 |
2 |
|
|
|
3 |
5 |
|
5 |
|
|
19 |
|
1 |
0 |
1 |
|
|
|
1 |
6 |
|
-1 |
|
|
20 |
|
0 |
1 |
-1 |
|
|
|
4 |
3 |
|
4 |
|
|
Рис. 2. Результати обчислень за внесеними формулами
3. ЗАВДАННЯ ДЛЯ РОЗВ’ЯЗУВАННЯ ЛІНІЙНОГО МАТРИЧНОГО РІВНЯННЯ
Задані матриці А та В . Розробити структуру таблиці на робочому аркуші та, використовуючи табличний процесор Excel, отримати розв’язок матричного лінійного рівняння
A X = B .
Результати роботи видрукувати.
Варіанти матриць А та В для проведення обчислень:
1 |
3 |
5 |
−2 |
17 |
3 |
|
1. A = 5 |
2 |
−2 , |
B = |
2 |
−7 |
16 |
3 |
1 |
−2 |
|
1 |
−6 |
10 |
5
|
1 |
|
2 |
|
3 |
|
|
|
7 |
|
3 |
|
|
|
|||
2. A = |
1 |
−3 |
|
2 , |
|
B = |
5 −3 |
|
|
|
|||||||
|
2 |
|
1 −1 |
|
|
|
0 |
−4 |
|
|
|
||||||
|
1 |
|
2 |
|
3 |
|
|
|
|
1 |
6 |
|
|
||||
3. A = |
1 |
−4 1 , |
|
|
B = |
−3 −4 |
|
|
|||||||||
|
2 |
−1 5 |
|
|
|
−2 |
|
5 |
|
|
|||||||
|
3 |
2 |
|
|
3 |
|
|
|
3 |
4 |
4 |
|
|
||||
4. A = |
1 |
1 |
|
2 , |
|
|
B = |
1 2 0 |
|
|
|||||||
|
2 |
1 −1 |
|
|
|
0 0 |
6 |
|
|
||||||||
5. |
1 |
|
2 |
|
|
|
|
3 |
|
0 |
|
7 |
|
||||
A = |
|
|
, |
|
|
B = |
−3 |
−6 − |
|
|
|
||||||
|
1 |
− |
4 |
|
|
|
|
11 |
|
||||||||
|
|
|
1 3 |
2 |
|
|
|
|
7 |
|
8 −2 |
||||||
6. A = −2 0 |
|
−2 , |
B = |
−6 −4 −4 |
|||||||||||||
|
|
|
2 2 −1 |
|
|
|
|
5 −3 |
|
5 |
|||||||
7. |
3 |
|
2 |
|
|
|
1 |
−1 |
|
1 |
|
|
|||||
A = |
1 |
|
, |
|
|
B = |
2 |
|
|
|
|
|
|||||
|
|
− |
1 |
|
|
|
|
3 −3 |
|
|
|||||||
|
4 |
2 |
3 |
|
|
|
|
5 |
2 |
|
|
|
|||||
8. |
|
1 |
2 |
|
|
, |
|
|
|
−3 |
− |
|
|
|
|
||
A = |
|
1 |
|
B = |
1 |
|
|
|
|||||||||
|
|
2 |
1 |
− |
|
|
|
|
|
0 |
|
|
|
|
|
||
|
|
1 |
|
|
|
|
|
1 |
|
|
|
||||||
9. |
3 |
|
2 |
|
|
|
8 |
3 |
11 |
|
|
||||||
A = |
5 |
|
2 |
, |
|
B = |
8 −11 |
|
|
|
|
||||||
|
|
− |
|
|
|
|
|
−3 |
|
|
|||||||
|
1 |
|
2 |
2 |
|
|
|
|
5 |
|
−2 |
|
|
||||
10. |
|
1 |
−4 |
|
, |
|
|
|
−1 |
|
4 |
|
|
|
|||
A = |
2 |
|
B = |
|
|
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
2 −6 |
|
|
|
|||
|
|
|
1 −1 |
|
|
|
|
|
|
|
|||||||
|
1 |
3 |
|
1 |
|
|
|
|
−2 11 |
6 |
|||||||
11. |
|
2 |
1 |
− |
|
|
|
|
|
−3 |
−6 |
6 |
|
||||
A = |
2 , |
|
|
B = |
|
||||||||||||
|
|
2 |
|
|
|
|
|
|
|
|
−3 |
|
|
|
|
||
|
|
2 −1 |
|
|
|
|
0 5 |
||||||||||
6
|
3 |
2 |
1 |
|
|
|
|
||
12. |
|
2 |
5 |
2 |
|
|
|
|
|
A = |
, |
|
|
||||||
|
|
2 |
1 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
13. |
5 |
7 |
|
|
|
|
|
|
|
A = |
3 |
, |
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
5 |
2 |
|
4 |
|
|
|||
14. |
|
1 |
2 |
|
|
, |
|
||
A = |
|
1 |
|
||||||
|
|
1 |
2 |
− |
|
|
|
||
|
|
1 |
|
|
|||||
|
1 |
3 |
|
5 |
|
||||
15. |
|
4 |
2 |
−2 |
|
|
|||
A = |
, |
|
|||||||
|
|
3 |
1 |
−2 |
|
|
|||
|
|
|
|
||||||
|
6 |
2 |
3 |
|
|
|
|
||
16. |
|
1 |
1 |
|
|
|
|
|
|
A = |
3 , |
|
|
|
|||||
|
|
2 |
2 |
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||
17. |
3 |
5 |
|
|
|
|
|
|
|
A = |
1 |
, |
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
3 |
2 |
|
3 |
|
|
|||
18. |
|
0 |
3 |
|
2 |
|
, |
|
|
A = |
|
|
|
||||||
|
|
2 |
1 |
|
|
|
|
|
|
|
|
−1 |
|
|
|||||
|
4 |
0 |
|
|
|
3 |
|
||
19. |
|
2 |
−3 |
|
|
|
|
|
, |
A = |
|
|
|
2 |
|||||
|
|
0 |
2 |
|
|
|
|
|
|
|
|
|
−1 |
|
|||||
|
1 |
3 |
|
5 |
|
|
|||
20. |
|
5 |
2 |
− |
2 |
|
, |
|
|
A = |
|
|
|||||||
|
|
3 |
1 |
− |
2 |
|
|
|
|
|
|
|
|
|
|||||
−2 |
7 |
|
|
|
||
|
−1 |
7 |
|
|
|
|
B = |
|
|
|
|
||
|
0 |
4 |
|
|
|
|
|
|
|
|
|
||
3 |
9 |
8 |
|
|
||
B = |
5 |
−1 |
|
|
|
|
|
8 |
|
|
|||
|
5 |
|
3 |
|
|
|
|
−2 |
−4 |
|
|
|
|
B = |
|
|
|
|||
|
−4 |
−6 |
|
|
|
|
|
|
|
|
|||
3 |
2 |
−1 |
|
|||
|
0 |
0 |
|
8 |
|
|
B = |
|
|
|
|||
|
0 |
−1 |
|
6 |
|
|
|
|
|
|
|||
−7 |
−5 |
|
|
|||
|
7 |
|
|
|
|
|
B = |
|
3 |
|
|
||
|
−1 |
|
|
|
|
|
|
|
1 |
|
|
||
1 |
9 |
−2 |
|
|
||
B = |
0 |
4 |
|
|
|
|
|
−1 |
|
|
|||
20 |
5 |
|
|
|
||
|
5 |
|
|
|
|
|
B = |
14 |
|
|
|
||
|
10 |
|
|
|
|
|
|
−1 |
|
|
|
||
15 |
|
7 |
|
|
||
|
−5 |
|
|
|
|
|
B = |
|
0 |
|
|
||
|
5 |
|
|
|
|
|
|
−1 |
|
|
|||
−2 |
17 |
|
3 |
|||
|
2 |
−7 |
16 |
|
||
B = |
|
|||||
|
1 |
−6 |
10 |
|
||
|
|
|||||
7
4. РОЗВ’ЯЗУВАННЯ НЕЛІНІЙНИХ АЛГЕБРАЇЧНИХ РІВНЯНЬ
У практиці інженерних обчислень досить часто доводиться розв’язувати алгебраїчні рівняння
F (x)= 0,
де функція F(x) - задана.
Складність задачі полягає у тому, що рівняння може мати один чи декілька дійсних розв’язків, або не мати жодного розв’язку. Зробити попередні висновки про кількість і наближені значення розв’язків рівняння можна, побу-
дувавши таблицю і графік функції y = F(x) для області визначення F(x), |
ви- |
||||||
користовуючи графічні можливості Excel. Точки перетину функції |
y = F(x) |
||||||
з віссю х |
відповідають розв’язкам рівняння F(x) = 0. |
|
|
|
|||
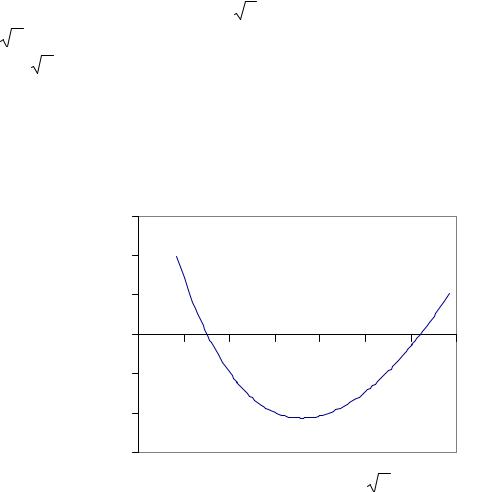
Наприклад, рівняння |
10sin |
x = 3x +5 , |
яке |
можна записати |
як |
||
10sin x −3x −5 = 0 , має |
два |
розв’язки, |
тому |
що графік |
функції |
||
y =10sin |
x −3x −5 двічі перетинає вісь х (рис. 3). |
|
|
хі, |
|||
У випадку, якщо розв’язок існує, потрібно визначити такі значення |
|||||||
підставивши які у рівняння замість х, отримаємо тотожності. На прикладі функції, показаної на рис. 3, видно, що розв’язки слід шукати в околі 0,5 та дещо більше ніж 1,4.
0,6 |
y |
|
|
|
|
|
|
|
0,4 |
|
|
|
|
|
|
|
|
0,2 |
|
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
x |
-0,2 0,2 |
0,4 |
0,6 |
0,8 |
1 |
1,2 |
1,4 |
1,6 |
|
-0,4 |
|
|
|
|
|
|
|
|
-0,6 |
|
|
|
|
|
|
|
|
|
Рис. 3. Графік функції y =10sin |
x −3x −5 |
||||||
Якщо розв’язок не вдається отримати аналітично, використовуємо методи наближеного розв’язання рівняння. Табличне представлення даних і результатів проміжних обчислень в Excel дозволяє реалізувати ітераційні розрахункові схеми, які виникають при застосуванні чисельних методів. Крім того, алгебраїчні рівняння можна розв’язувати в Excel, використовуючи вбудований у програму допоміжний засіб – “Пошук розв’язку”.
8

4.1. Реалізація ітераційної розрахункової схеми в електронній таблиці
Для того, щоб застосувати відомі методи чисельного розв’язання рівняння F(x) = 0, потрібно спочатку перетворити його до вигляду
x = f (x) .
Іноді це досить легко зробити. Наприклад, рівняння 10sin  x −3x −5 = 0 відповідним перетворенням рівняння набуває вигляду
x −3x −5 = 0 відповідним перетворенням рівняння набуває вигляду
x = |
10sin x −5 |
, тобто f (x) = 10sin |
x −5 . |
|
3 |
|
3 |
Тоді з області визначення функції f(x) вибирається певне значення x = x0 , яке відіграє роль початкового наближення. Це значення підставляємо у праву частину рівняння і отримуємо наближення x = x1
x1 = f (x0 ) .
Наступні наближення обчислюються подібним чином xn+1 = f (xn ) .
Якщо із зростанням n попереднє і наступне значення х зближуються, тобто xn+1 − xn → 0, то ітераційний процес збігається і наближений
розв’язок отримано.
Сплануємо наступне заповнення робочого аркуша для реалізації цієї розрахункової схеми (рис. 4.)
|
A |
B |
С |
|
1 |
Ітераційний метод розв' |
язування рівняння x = f(x) |
||
2 |
Послідовні наближення розв’язку |
|
||
3 |
Попереднє значення |
|
Наступне значення |
Похибка розв’язку |
|
хn |
|
хn+1 |
│хn+1– хn│ |
4 |
х0 |
|
f(х0) |
│х1 – х0│ |
5 |
х1 |
|
f(х1) |
│х2 – х1│ |
6 |
… |
|
… |
… |
7 |
|
|
|
|
|
Рис. 4. Розташування даних і формул у комірках таблиці |
|||
При такому розташуванні даних у комірку А4 вносимо початкове значення х0. У комірці В4 обчислюємо значення f(х0). Це значення вносимо в комірку А5 і у комірці В5 обчислюємо наступне значення f(х1). Наближення розв’язку рівняння контролюємо у комірках стовпчика С. Рядки таблиці заповнюємо доти, поки у стовпчику С отримаємо мале значення, яке відповідає задовільній точності розв’язання рівняння.
9
Приклад. Застосуємо таку структуру таблиці для розв’язання рівняння
10sin x −3x −5 = 0 , записаного у вигляді |
x = |
10sin x −5 . |
|
|
3 |
Допустимими значеннями х тут є значення x ≥ 0 , з яких вибираємо початкове наближення x = x0 , наприклад x0 =1, і далі отримуємо наступні наближення згідно з формулою
|
xn+1 = |
10sin |
|
xn −5 |
. |
|
|
|
3 |
|
|
||
|
|
|
|
|
|
|
Для цього прикладу створюємо електронну таблицю (рис. 5). |
||||||
|
|
|
|
|
|
|
A |
|
B |
|
|
|
С |
1Ітераційний метод розв'язування рівняння 10sin  x −3x −5 = 0
x −3x −5 = 0
2Послідовні наближення розв’язку
3 |
Попереднє значення |
Наступне значення хn+1 |
Похибка розв’язку |
|
|
|
хn |
|
│ хn+1- хn │ |
4 |
|
1 |
=(10*SIN(КОРЕНЬ(A4))-5)/3 |
=ABS(A4-B4) |
5 |
|
=B4 |
=(10*SIN(КОРЕНЬ (A5))-5)/3 |
=ABS(A5-B5) |
6 |
|
=B5 |
=(10*SIN(КОРЕНЬ (A6))-5)/3 |
=ABS(A6-B6) |
7 |
|
… |
… |
… |
Рис. 5. Розрахункові формули задачі в комірках робочого аркуша |
||||
Послідовність заповнення таблиці. |
|
|||
1. Вносимо дані у комірки таблиці |
|
|||
|
А4 |
1 |
|
|
|
В4 |
=(10*SIN(КОРЕНЬ(A4))-5)/3 |
|
|
|
С4 |
=ABS(B4-A4) |
|
|
|
А5 |
=B4 |
|
|
Функцію КОРЕНЬ вносимо у формулу, використовуючи майстер функцій.
2. Копіюємо формули у стовпчиках А, В, та С у наступні рядки таблиці, використовуючи автозаповнення. Для цього наводимо курсор миші на нижній кут комірки з формулою і при натиснутій лівій клавіші миші протягуємо маркер заповнення на кілька комірок вниз. Після цього відпускаємо клавішу миші. Формули скопіюються з модифікацією у них відносних адрес комірок. Кількість рядків таблиці збільшуємо поки не досягнемо потрібної точності обчислень, тобто коли похибка розв’язку у стовпчику С достатньо мала. При цьому значення у стовпчиках А та В достатньо близькі і отримане значення у стовпчику В приймаємо за розв’язок рівняння (рис. 6).
З таблиці (рис. 6) випливає, що ітераційний процес збіжний, оскільки у стовпчику С відхилення лівої і правої частин рівняння спадає. Розв’язок рів-
10
