
- •Интерференция световых волн.
- •Ширина интерференционных полос
- •Способы получения когерентных волн делением волнового фронта:
- •7. Области применения интерференции.
- •8. Принцип Гюйгенса-Френеля.
- •9. Метод зон Френеля.
- •10. Метод графического сложения амплитуд
- •11. Дифракция Френеля от простейших преград
- •12. Дифракция Френеля на полуплоскости. Спираль Корню.
- •13. Дифракция Фраунгофера от одной щели
- •14 .Дифракция Фраунгофера от двух щелей:
- •2 Способ
- •15. Дифракция света от прямоугольного и круглого отверстия
- •16. Дифракционная решетка
- •17. Дифракция на двумерной решетке.
- •18. Дифракция на трехмерной решетке.
- •20. Понятие о голографии
11. Дифракция Френеля от простейших преград
Дифракция света- явление отклонения света от прямолинейного направления распространения при прохождении вблизи препятствий.
а) Дифракция от круглого отверстия
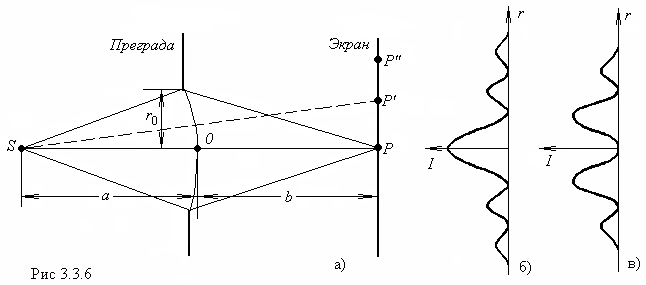
Поставим
на пути сферической световой волны
непрозрачный экран с вырезанным в нем
круглым отверстием радиуса ![]() .
Расположим экран так, чтобы перпендикуляр,
опущенный из источника света
.
Расположим экран так, чтобы перпендикуляр,
опущенный из источника света![]() ,
попал в центр отверстия (рис.3.3. 6). На
продолжении этого перпендикуляра
возьмем точку
,
попал в центр отверстия (рис.3.3. 6). На
продолжении этого перпендикуляра
возьмем точку![]() .
При радиусе отверстия
,
значительно меньшем, чем указанные на
рисунке длины
.
При радиусе отверстия
,
значительно меньшем, чем указанные на
рисунке длины ![]() и
и![]() ,
длину
можно
считать равной расстоянию от источника
до
преграды, а длину
-
расстоянию от преграды до точки
.
Если расстояния
и
удовлетворяют
соотношению:
,
длину
можно
считать равной расстоянию от источника
до
преграды, а длину
-
расстоянию от преграды до точки
.
Если расстояния
и
удовлетворяют
соотношению:
![]()
где ![]() -
целое число, то отверстие оставит
открытыми ровно
первых
зон Френеля, построенных для точки
.
-
целое число, то отверстие оставит
открытыми ровно
первых
зон Френеля, построенных для точки
.
Число
открытых зон Френеля определяется
выражением

Амплитуда
в точке
будет
равна
![]()
Перед ![]() берется
знак плюс, если
нечетное,
и минус, если
четное.
Положив выражения в скобках равными
нулю, придем к формулам
берется
знак плюс, если
нечетное,
и минус, если
четное.
Положив выражения в скобках равными
нулю, придем к формулам
![]() m
нечетное
m
нечетное
![]() m
четное
m
четное
Амплитуды
от двух соседних зон практически
одинаковы. Поэтому
![]() можно заменить через
можно заменить через

В
результате получится

Картина дифракции на круглом отверстии: 1-отверстие открывает нечетное число зон, в центре - свет, 2- отверстие открывает четное число зон, в центре - темнота.

б) Дифракция от круглого диска

Поместим между источником света и точкой наблюдения непрозрачный круглый диск радиуса (рис.3.3.8). Если диск закроет
![]() первых
зон Френеля, амплитуда в точке
будет
равна
первых
зон Френеля, амплитуда в точке
будет
равна
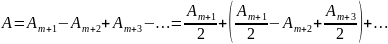
Выражения, стоящие в скобках, можно положить равными 0, значит
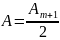
Картина дифракции на круглом диске: Светлое пятно в центре- пятно Пуассона

12. Дифракция Френеля на полуплоскости. Спираль Корню.
Поместим
на пути световой волны (которую для
простоты будем считать плоской)
непрозрачную полуплоскость с прямолинейным
краем. Расположим эту полуплоскость
так, чтобы она совпала с одной из волновых
поверхностей. На расстоянии
за
полуплоскостью поставим параллельный
ей экран, на котором возьмем точку
(рис.
3.3.9). Разобьем открытую часть волновой
поверхности на зоны, имеющие вид очень
узких прямолинейных полосок, параллельных
краю полуплоскости. Ширину зон выберем
так, чтобы отсчитанные в плоскости
рисунка расстояния от точки
до
краев любой зоны отличались на одинаковую
величину ![]() .
При этом условии колебания, создаваемые
в точке
соседними
зонами, будут отличаться по фазе на
постоянную величину.
.
При этом условии колебания, создаваемые
в точке
соседними
зонами, будут отличаться по фазе на
постоянную величину.
Зонам,
расположенным справа от точки
,
припишем номера1, 2, 3 и т. д., расположенным
слева - номера 1', 2', 3' и т. д. Зоны с
номерами
и![]() имеют
одинаковую ширину и расположены
относительно точки
симметрично.
Поэтому создаваемые имив
колебания
совпадают по амплитуде и по фазе.
имеют
одинаковую ширину и расположены
относительно точки
симметрично.
Поэтому создаваемые имив
колебания
совпадают по амплитуде и по фазе.
 Чтобы
установить зависимость амплитуды от
номера зоны
,
оценим площади зон. Из рис. 3.3.10 видно,
что суммарная ширина первых
зон
равна
Чтобы
установить зависимость амплитуды от
номера зоны
,
оценим площади зон. Из рис. 3.3.10 видно,
что суммарная ширина первых
зон
равна
![]()
Вследствие
узости зон![]() .
Поэтому при не очень больших
квадратичным
членом под корнем можно пренебречь.
Тогда
.
Поэтому при не очень больших
квадратичным
членом под корнем можно пренебречь.
Тогда
![]() .
.
Положив
в этой формуле ![]() ,
получим, что
,
получим, что![]() .
Следовательно, выражению для суммарной
ширины первых
зон
можно придать вид
.
Следовательно, выражению для суммарной
ширины первых
зон
можно придать вид
![]() .
.
Отсюда
![]() .
.
Расчет
по последней формуле дает, что
![]() В
таких же соотношениях находятся и
площади зон.
В
таких же соотношениях находятся и
площади зон.
 Из
последнего соотношения вытекает, что
амплитуда колебаний, создаваемых в
точке
отдельными
зонами, в начале (для первых зон) убывает
очень быстро, затем это убывание
становится медленным. По этой причине
ломаная линия, получающаяся при
графическом сложении колебаний,
возбуждаемых прямолинейными зонами,
идет сначала более полого, чем в
случае кольцевых зон (площади которых
при аналогичном построении примерно
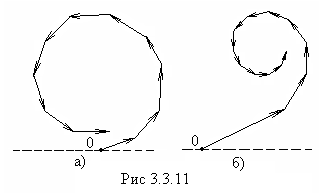
равны). На рис. 3.3.11 сопоставлены обе
векторные диаграммы. В обоих случаях
отставание по фазе каждого следующего
колебания взято одним и тем же.
Из
последнего соотношения вытекает, что
амплитуда колебаний, создаваемых в
точке
отдельными
зонами, в начале (для первых зон) убывает
очень быстро, затем это убывание
становится медленным. По этой причине
ломаная линия, получающаяся при
графическом сложении колебаний,
возбуждаемых прямолинейными зонами,
идет сначала более полого, чем в
случае кольцевых зон (площади которых
при аналогичном построении примерно
равны). На рис. 3.3.11 сопоставлены обе
векторные диаграммы. В обоих случаях
отставание по фазе каждого следующего
колебания взято одним и тем же.
Значение
амплитуды для кольцевых зон (рис.3.3.11,
а) принято постоянным, а для прямолинейных
зон (рис.3.3.11, б) - убывающим в соответствии
с последним соотношением. Графики на
рис.3.3.11 являются приближенными. При
точном построении графиков нужно
учитывать зависимость амплитуды
от ![]() и
и![]() .Однако
на общем характере диаграмм это не
отразится.
.Однако
на общем характере диаграмм это не
отразится.
На рис.3.3.11, б показаны только колебания, обусловленные зонами, лежащими справа от точки . Зоны с номерами и расположены симметрично относительно .
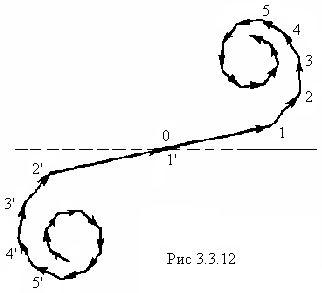 Поэтому
естественно при построении диаграммы
векторы, изображающие соответствующие
этим зонам колебания, располагать
симметрично относительно начала
координат
Поэтому
естественно при построении диаграммы
векторы, изображающие соответствующие
этим зонам колебания, располагать
симметрично относительно начала
координат ![]() (рис.3.3.12).
Если ширину зон устремить к нулю,
ломаная линия, изображенная на рис.
3.3.12, превратится в плавную кривую
(рис. 3.3.13), которая называется спиралью
Корню.
(рис.3.3.12).
Если ширину зон устремить к нулю,
ломаная линия, изображенная на рис.
3.3.12, превратится в плавную кривую
(рис. 3.3.13), которая называется спиралью
Корню.
У равнение
спирали Корню в параметрической форме
равнение
спирали Корню в параметрической форме
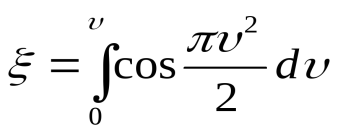

Эти
интегралы называются интегралами
Френеля. Они не берутся в элементарных
функциях, однако имеются таблицы, по
которым можно находить значения
интегралов для разных ![]() .
.
Смысл
параметра
заключается
в том, что ![]() дает
длину дугикривой Корню, измеряемую от
начала координат.
дает
длину дугикривой Корню, измеряемую от
начала координат.
Числа,
отмеченные вдоль кривой на рис. 3.3.13,
дают значения параметра
.
Точки ![]() и
и![]() ,
к которым асимптотически приближается
кривая при стремлении
к
,
к которым асимптотически приближается
кривая при стремлении
к ![]() и
и![]() ,
называются фокусами или полюсами
спирали Корню. Их координаты равны
,
называются фокусами или полюсами
спирали Корню. Их координаты равны
![]()
![]() для
точки F1
для
точки F1
![]()
![]() для
точки F2
для
точки F2
Правый
завиток спирали (участок ![]() )
соответствует зонам, расположенным
справа от точки
,
левый завиток (участок
)
соответствует зонам, расположенным
справа от точки
,
левый завиток (участок![]() )
-зонам, расположенным слева от точки
.
)
-зонам, расположенным слева от точки
.
Найдем
производную ![]() в
точке кривой, отвечающей данному
значению параметра
.
Приращению
на
в
точке кривой, отвечающей данному
значению параметра
.
Приращению
на ![]() соответствует
соответствует
![]()
![]()
Следовательно, ![]() .
Вместе с тем
.
Вместе с тем![]() ,
где
,
где![]() -
угол наклона касательной к кривой в
данной точке. Таким образом,
-
угол наклона касательной к кривой в
данной точке. Таким образом,![]() .
.
Отсюда
следует, что в точке, отвечающей ![]() ,
касательная к кривой Корню
перпендикулярна к оси
,
касательная к кривой Корню
перпендикулярна к оси ![]() .
При
.
При![]() угол
равен
угол
равен![]() ,так
что касательная параллельна оси
.
При
,так
что касательная параллельна оси
.
При![]() угол
равен
угол
равен![]() ,
так что касательная снова перпендикулярна
к оси
,
и т. д.
,
так что касательная снова перпендикулярна
к оси
,
и т. д.
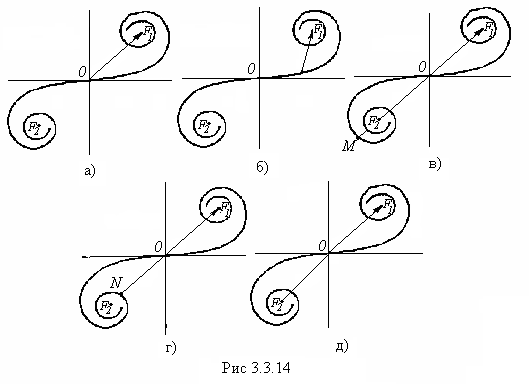 Спираль
Корню дает возможность найти амплитуду
светового колебания в любой точке
экрана. Положение точки будем
характеризовать координатой
Спираль
Корню дает возможность найти амплитуду
светового колебания в любой точке
экрана. Положение точки будем
характеризовать координатой ![]() ,
отсчитываемой от границы геометрической
тени (см. рис. 3.3.9).Для точки
,
лежащей на границе геометрической
тени
,
отсчитываемой от границы геометрической
тени (см. рис. 3.3.9).Для точки
,
лежащей на границе геометрической
тени ![]() ,
все штрихованные зоны будут закрыты.
Колебаниям от не штрихованных зон
соответствует правый завиток спирали.
Следовательно, результирующее колебание
изобразится вектором, начало которого
находится в точке
,
а конец - в точке
(рис.
3.3.14, а). При смещении точки
в
область геометрической тени полуплоскость
закрывает все большее число не штрихованных
зон. Поэтому начало результирующего
вектора перемещается по правому завитку
в направлении полюса F1 (рис.
3.3.14, б). В результате амплитуда
колебания монотонно стремится к нулю.
,
все штрихованные зоны будут закрыты.
Колебаниям от не штрихованных зон
соответствует правый завиток спирали.
Следовательно, результирующее колебание
изобразится вектором, начало которого
находится в точке
,
а конец - в точке
(рис.
3.3.14, а). При смещении точки
в
область геометрической тени полуплоскость
закрывает все большее число не штрихованных
зон. Поэтому начало результирующего
вектора перемещается по правому завитку
в направлении полюса F1 (рис.
3.3.14, б). В результате амплитуда
колебания монотонно стремится к нулю.
Если
точка
смещается
от границы геометрической тени вправо,
в дополнение к не штрихованным зонам
открывается все возрастающее число
штрихованных зон. Поэтому начало
результирующего вектора скользит
по левому завитку спирали в направлении
к полюсу
.
При этом амплитуда проходит через ряд
максимумов(первый из них равен длине
отрезка ![]() на
рис.3.3.14, в) и минимумов (первый из них
равен длине отрезка
на
рис.3.3.14, в) и минимумов (первый из них
равен длине отрезка ![]() на
рис. 3.3.14, г).При полностью открытой
волновой поверхности амплитуда равна
длине отрезка
на
рис. 3.3.14, г).При полностью открытой
волновой поверхности амплитуда равна
длине отрезка ![]() (рис.
3.3.14, д), т. е. ровно в два раза превышает
амплитуду на границе геометрической
тени (см. рис. 3.3.14, а). Соответственно
интенсивность на границе геометрической
тени составляет 1/4 интенсивности
(рис.
3.3.14, д), т. е. ровно в два раза превышает
амплитуду на границе геометрической
тени (см. рис. 3.3.14, а). Соответственно
интенсивность на границе геометрической
тени составляет 1/4 интенсивности ![]() ,
получающейся на экране в отсутствие
преград.
,
получающейся на экране в отсутствие
преград.
 Зависимость
интенсивности света
Зависимость
интенсивности света ![]() от
координаты
дана
нарис. 3.3.15. При переходе в область
геометрической тени интенсивность
изменяется не скачком, а постепенно
стремится к нулю. Справа от границы
геометрической тени расположен ряд
чередующихся максимумов и минимумов
интенсивности.
от
координаты
дана
нарис. 3.3.15. При переходе в область
геометрической тени интенсивность
изменяется не скачком, а постепенно
стремится к нулю. Справа от границы
геометрической тени расположен ряд
чередующихся максимумов и минимумов
интенсивности.
