
Частина 2
.pdf
“Курс вищої математики. Частина 2.”
Q(xi-1)
Q(xi)
а xi-1 xi b x
Хай є тіло об'єму V. Площа будь-якого поперечного перетину тіла Q, відома як безперервна функція Q = Q(x). Розіб'ємо тіло на “шари” поперечними перетинами, що проходять через точки хi розбиття відрізання [а, b]. Оскільки на какомабо проміжному відрізку розбиття [xi-1, xi] функція Q(x) безперервна, то приймає на нім найбільше і найменше значення. Позначимо їх відповідно Mi і mi.
Якщо на цих найбільшому і найменшому перетинах побудувати циліндри із створюючими, паралельними осі х, то об'єми цих циліндрів будуть відповідно рівні
Mixi і mixi тут xi = xi - xi-1. |
|
Провівши такі побудови для |
всіх відрізань розбиття, отримаємо циліндри, |
n |
n |
об'єми яких рівні відповідно ∑M i ∆xi |
і ∑mi ∆xi . |
i=1 |
i=1 |
При прагненні до нуля кроку розбиття, ці суми мають загальну межу:
|
n |
n |
b |
limλ→0 |
∑M i ∆xi = limλ→0 |
∑mi ∆xi = ∫Q(x)dx |
|
|
i=1 |
i=1 |
a |
Таким чином, об'єм тіла може бути знайдений по формулі:
b
V = ∫Q(x)dx
a
Недоліком цієї формули є те, що для знаходження об'єму необхідно знати функцію Q(x), що вельми проблематично для складних тіл.
Приклад: Знайти об'єм кулі радіусу R.
у
R у
-R |
0 |
x R |
x |
У поперечних перетинах кулі виходять кола змінного радіусу у. Залежно від поточної координати х цей радіус виражається по формулі  R2 − x2 .
R2 − x2 .
Тоді функція площ перетинів має вигляд: Q(x)= π(R2 − x2 ). Отримуємо об'єм кулі:
81
“Курс вищої математики. Частина 2.”
R |
|
|
|
|
|
|
|
x |
3 |
|
R |
|
|
|
R |
3 |
|
|
|
|
|
R |
3 |
|
|
4πR |
3 |
|
V = ∫ |
π(R |
2 |
− x |
2 |
)dx = π(R |
2 |
x − |
|
|
|
|
3 |
|
|
|
|
− R |
3 |
|
|
|
|
|
|
||||
|
|
|
|
|
) |
|
|
− |
|
|
|
+ |
|
|
= |
|
. |
|||||||||||
|
|
|
3 |
|
= π R |
|
3 |
|
− π |
|
3 |
|
3 |
|||||||||||||||
−R |
|
|
|
|
|
|
|
−R |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Приклад: Знайти об'єм довільної піраміди з висотою Н і площею підстави S.
QS
xH x
При перетині піраміди площинами, перпендикулярними висоті, в перетині отримуємо фігури, подібні до підстави. Коефіцієнт подібності цих фігур рівний відношенню x/H, де х – відстань від площини перетину до вершини піраміди.
З геометрії відомо, що відношення площ подібних фігур рівне коефіцієнту подібності в квадраті, тобто
Q |
|
x 2 |
|
|
= |
|
|
S |
|
||
|
H |
||
Звідси отримуємо функцію площ перетинів: Знаходимо об'єм піраміди:
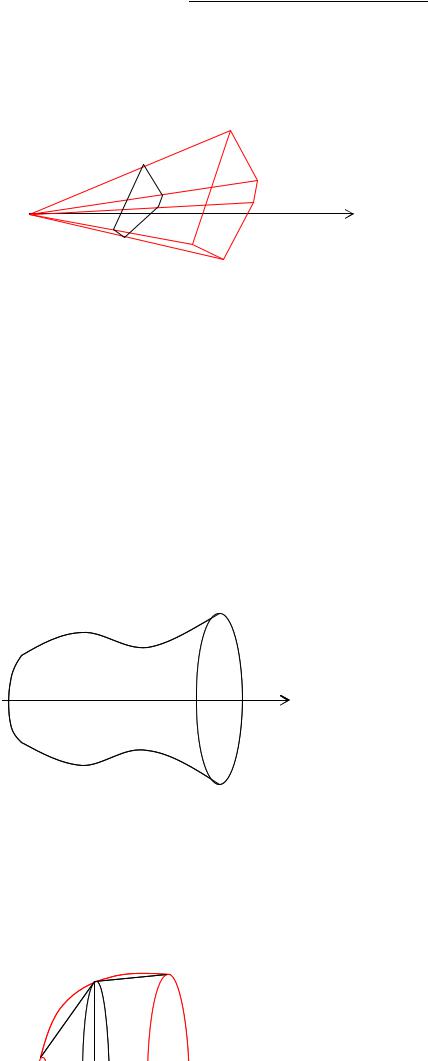
Об'єм тіл обертання.
Розглянемо криву, задану рівнянням у = f(x). Припустимо, що функція f(x) безперервна на відрізку [а, b]. Якщо відповідну їй криволінійну трапецію з підставами а
іb обертати навколо осі Ох, то отримаємо так зване тіло обертання.
у= f(x)
x
Оскільки кожен перетин тіла площиною x = const є кругом радіусу, то об'єм тіла обертання може бути легко знайдений по отриманій вище формулі:
b
V = π∫ f 2 (x)dx
a
Площа поверхні тіла обертання.
Мi B
82

“Курс вищої математики. Частина 2.”
А
х
xi
Визначення: Площею поверхні обертання кривої АВ навколо даної осі називають межу, до якої прагнуть площі поверхонь обертання ламаних, вписаних в криву АВ, при прагненні до нуля найбільших з довжин ланок цих ламаних.
Розіб'ємо дугу АВ на n частин точками M0, M1, M2 ., Mn. Координати вершин отриманою ламаною мають координати xi і yi. При обертанні ламаної навколо осі отримаємо поверхню, що складається з бічних поверхонь усічених конусів, площа яких рівна Pi. Ця площа може бути знайдена по формулі:
∆P = 2π |
yi−1 + yi |
∆S |
i |
|
||||
|
|
|||||||
i |
|
|
2 |
|
|
|
|
|
Тут Si – довжина кожної хорди. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
2 |
2 |
= |
|
|
∆yi |
∆xi |
||
∆Si = ∆xi |
+ ∆yi |
1 + |
|
|
||||
|
|
|
|
|
|
∆xi |
|
|
Застосовуємо теорему Лагранжа (див. Теорема Лагранжа.) до відношення
Отримуємо: Тоді
∆Pi = 2π yi−1 + yi |
1 + f ′2 (εi )∆xi |
2 |
|
∆yi . ∆xi
Площа поверхні, описаної ламаної рівна:
|
|
|
|
|
|
n |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Pn = π∑(f (xi−1 ) + f (xi )) 1 + f |
′2 (εi )∆xi |
|
|
|
|
||||||
|
|
|
|
|
|
i=1 |
|
|
|
|
|
|
|
|
|
|
Ця сума не є інтегральною, але можна показати, що |
|
|
|
|
|
|
||||||||||
P = lim |
π n |
(f (x |
i−1 |
) + f (x |
)) 1 + f ′2 (ε |
)∆x |
i |
= |
lim |
π n |
2 f (ε |
) |
1 + f ′2 (ε |
)∆x |
i |
|
max ∆x →0 |
∑ |
|
|
i |
i |
|
|
max ∆x →0 |
∑ |
i |
|
i |
|
|||
i |
i=1 |
|
|
|
|
|
|
|
|
i |
i=1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Тоді P = 2π∫ f (x) |
1 + f ′2 (x)dx - формула обчислення площі поверхні тіла обертання. |
|||||||||||||||
a
Функції декілька змінних
83

“Курс вищої математики. Частина 2.”
При розгляді функцій декілька змінних обмежимося докладним описом функцій два змінних, оскільки всі отримані результати будуть справедливі для функцій довільного числа змінних.
Визначення: Якщо кожній парі незалежних один від одного чисел (х, у) з деякої множини по якому - або правилу ставиться у відповідність одне або декілька значень змінної z, то змінна z називається функцією два змінних.
z = f(x, у)
Визначення: Якщо парі чисел (х, у) відповідає одне значення z, то функція називається однозначною, а якщо більш за одне, то – багатозначною.
Визначення: Областю визначення функції z називається сукупність пар (х, у), при яких функція z існує.
Визначення: Околицею точки М0(х0, у0) радіусу r називається сукупність всіх крапок (х, у), які задовольняють умові (x − x0 )2 + (y − y0 )2 < r .
Визначення: Число А називається межею функції f(x, у) при прагненні крапки М(х, у) до точки М0(х0, у0), якщо для кожного числа ε > 0 знайдеться таке число r >0, що для будь-якої точки М(х, у), для яких вірна умова
MM 0 < r
також вірно і умова f (x, y) − A < ε . Записують:
Визначення: Хай точка М0(х0, у0) належить області визначення функції f(x, у). Тоді функція z = f(x, у) називається безперервною в точці М0(х0, у0), якщо
lim f (x, y) = f (x0 , y0 ) (1)
x→x0 y→y0
причому точка М(х, у) прагне до точки М0(х0, у0) довільним чином.
Якщо в якій – або крапці умова (1) не виконується, то ця крапка називається точкою розриву функції f(x, у). Це може бути в наступних випадках:
1) Функція z = f(x, у) не визначена в точці М0(х0, у0).
2) Не існує межа lim f (x, y) .
x→x0 y→y0
3) Ця межа існує, але він не рівний f( x0, y0).
Властивість. Якщо функція f(x, у .) визначена і безперервна в замкнутій і обмеженій області D, то в цій області знайдеться принаймні одна крапка
N(x0, y0 .), така, що для решти крапок вірна нерівність f(x0, y0 .) ≥ f(x, у .)
а також точка N1(x01, y01 .), така, що для решти всіх крапок вірна нерівність f(x01, y01 .) ≤ f(x, у .)
тоді f(x0, y0 .)= M – найбільше значення функції, а f(x01, y01 .)= m – найменше значення функції f(x, у .) в області D.
Безперервна функція в замкнутій і обмеженій області D досягає принаймні один раз найбільшого значення і один раз найменшого.
84

“Курс вищої математики. Частина 2.”
Властивість. Якщо функція f(x, у .) визначена і безперервна в замкнутій обмеженій області D, а M і m – відповідно найбільше і найменше значення функції в цій області, то для будь-якої крапки існує крапка
N0(x0, y0 .) така, що f(x0, y0 .)= µ.
Простіше кажучи, безперервна функція приймає в області D всі проміжні значення між M і m. Наслідком цієї властивості може служити висновок, що якщо числа M і m різних знаків, то в області D функція принаймні один раз звертається в нуль.
Властивість. Функція f(x, у .), безперервна в замкнутій обмеженій області D, обмежена в цій області, якщо існує таке число До, що для всіх точок області вірна нерівність f (x, y,...) < K .
Властивість. Якщо функція f(x, у .) визначена і безперервна в замкнутій обмеженій області D, то вона рівномірно безперервна в цій області, тобто для будьякого позитивного числа ε існує таке число ∆ > 0, що для будь-яких двох крапок (х1, y1) і (х2, у2) області, що знаходяться на відстані, меншому, виконана нерівність
f (x1 , y1 ) − f (x2 , y2 ) < ε
Приведені вище властивості аналогічні властивостям функцій однієї змінної, безперервних на відрізку. Див. Свойства функций, непрерывных на отрезке.
Похідні і диференціали функцій декількох змінних.
Визначення. Хай в деякій області задана функція z = f(x, у). Візьмемо довільну
точку М(х, у) і задамо приріст х до змінній х. Тоді величина xz = f( x + ∆x, у) – f(x, у)
називається приватним приростом функції по х.
Можна записати
|
|
|
∆x z = |
f (x + ∆x, y) − f (x, y) |
. |
|
|
|
|||
|
|
|
∆x |
∆x |
|
|
|||||
Тоді lim |
∆x z |
називається приватній похідній функції z = f(x, у) по х. |
|||||||||
∆x→0 |
∆x |
|
|
|
|
|
|
|
|
|
|
Позначення: |
|
|
|
|
|
|
|
|
|
|
|
Аналогічно визначається приватна похідна функції по у. |
|
|
|||||||||
|
|
|
∂z |
= lim |
f (x, y + ∆y) − f (x, y) |
|
|
|
|||
|
|
|
∂y |
|
|
|
|||||
|
|
|
∆y→0 |
∆y |
|
|
|||||
Геометричним сенсом |
приватної |
похідної (допустимо |
∂z |
) є тангенс кута |
|||||||
|
|
|
|
|
|
|
|
|
|
∂x |
|
нахилу дотичної, проведеної в точці N0(x0, y0, z0) до перетину поверхні площиною у =
у0.
85

“Курс вищої математики. Частина 2.”
Повний приріст і повний диференціал.
Визначення. Для функції f(x, у) вираз z = f( x + ∆x, у + ∆у) – f(x, у) називається
повним приростом.
Якщо функція f(x, у) має безперервні приватні похідні, то |
|
||||||
∆z = f (x + ∆x, y + ∆y) − f (x, y) + f (x, y + ∆y) − f (x, y + ∆y) = [f (x + ∆x, y + ∆y) − f (x, y + ∆y)]+ |
|||||||
+[f (x, y + ∆y) − f (x, y)] |
|
|
|
|
|
|
|
Застосуємо теорему Лагранжа (див. Теорема Лагранжа.) до виразів, що стоять в |
|||||||
квадратних дужках. |
|
|
|
|
|
|
|
f (x, y + ∆y) − f (x, y) = ∆y ∂f (x, y) |
|
||||||
|
|
|
|
|
∂y |
|
|
f (x + ∆x, y + ∆y) − f (x, y + ∆y) = ∆x ∂f (x, y + ∆y) |
|
||||||
тут |
|
|
|
|
∂x |
|
|
|
|
|
|
|
|
||
Тоді отримуємо |
|
|
|
|
|
|
|
∆z = ∆x ∂f (x, y + ∆y) + ∆y ∂f (x, y) |
|
||||||
|
|
∂x |
|
∂y |
|
||
Оскільки приватні похідні безперервні, то можна записати рівність: |
|
||||||
lim ∂f (x, y + ∆y) |
= ∂f (x, y) |
|
|||||
∆x→0 |
∂x |
|
∂x |
|
|||
∆y→0 |
|
|
|
|
|
|
|
lim |
∂f (x, y) = |
∂f (x, y) |
|
||||
∆x→0 |
∂y |
|
∂y |
|
|||
∆y→0 |
|
|
|
|
|
|
|
Визначення. Вираз ∆z = |
∂f (x, y) |
∆x + |
∂f (x, y) |
∆y + α1∆x + α2 ∆y |
називається |
||
|
|
||||||
|
|
∂x |
|
∂y |
|
||
повним приростом функції f(x, у) в деякій крапці (х, у), де 1 і 2 – нескінченно малі функції при х → 0 і у → 0 відповідно.
Визначення: Повним диференціалом функції z = f(x, у) називається головна лінійна відносно х і у приросту функції z в крапці (х, у).
dz = f x′(x, y)dx + f y′(x, y)dy
Для функції довільного числа змінних:
df (x, y, z,...,t) = ∂∂fx dx + ∂∂fy dy +... + ∂∂ft dt
Приклад. Знайти повний диференціал функції u = x y2 z .
du = ∂∂ux dx + ∂∂uy dy + ∂∂uz dz
86

“Курс вищої математики. Частина 2.”
∂u |
= y 2 zx y2 z−1 ; |
∂u |
= x y2 z ln x 2 yz; |
∂u |
= x y2 z ln x y 2 ; |
∂x |
|
∂y |
|
∂z |
|
du = y 2 zx y2 z−1dx + 2x y2 z yz ln xdy + y2 x y2 z ln xdz
Приклад. Знайти повний диференціал функції
|
|
|
|
|
|
|
∂z = |
|
|
|
− 2 yx |
|
|
|
|
|
|
|
|
|
|||
∂z = |
y (x |
|
− y |
|
|
∂x |
|
(x2 − y 2 )2 |
+ 2 y |
|
= |
x |
|
+ y |
|
||||||||
|
|
) − y(−2 y) |
= x |
|
− y |
|
|
|
|
|
|||||||||||||
|
|
′ |
2 |
|
2 |
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
|
|
2 |
|
2 |
|
∂y |
|
|
|
(x2 − y 2 )2 |
|
|
|
|
|
(x2 − y 2 )2 |
|
|
(x2 − y 2 )2 |
||||||||||
|
|
|
|
dz = − |
2xy |
|
|
|
dx + |
x2 + y 2 |
|
dy |
|
|
|
|
|||||||
|
|
|
|
(x2 − y |
2 ) |
(x2 |
− y 2 ) |
2 |
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
Геометричний сенс повного диференціала. Дотична площина і нормаль до поверхні.
N
ϕN0
дотична площина
Хай N і N0 – точки даної поверхні. Проведемо пряму NN0. Площина, яка проходить через точку N0, називається дотичною площиною до поверхні, якщо кут між січною NN0 і цією площиною прагне до нуля, коли прагне до нуля відстань NN0.
Визначення. Нормаллю до поверхні в точці N0 називається пряма, що проходить через точку N0 перпендикулярно дотичній площині до цієї поверхні.
Уякій – або крапці поверхня має, або тільки одну дотичну площину, або не має
їїзовсім.
Якщо поверхня задана рівнянням z = f(x, у), де f(x, у) – функція, що диференціюється в точці М0(х0, у0), дотична площина в точці N0(x0,y0(x0,y0)) існує і має рівняння:
z − f (x0 , y0 ) = f x′(x0 , y0 )(x − x0 ) + f y′(x0 , y0 )( y − y0 ) .
87

|
|
|
|
|
|
“Курс вищої математики. Частина 2.” |
|
Рівняння нормалі до поверхні в цій крапці: |
|
|
|
|
|||
|
x − x0 |
= |
y − y0 |
= z − z0 |
|||
|
f x′(x0 y0 ) |
|
f y′(x0 , y0 ) |
|
|
−1 |
|
Геометричним сенсом повного диференціала функції два змінних f(x, у) в крапці (х0, у0) є приріст аплікати (координати z) дотичної площини до поверхні при переході від крапки (х0, у0) до крапки (х0+х, у0+у).
Як видно, геометричний сенс повного диференціала функції два змінних є просторовим аналогом геометричного сенсу диференціала функції однієї змінної.
Приклад. Знайти рівняння дотичної площини і нормалі до поверхні z = x2 − 2xy + y 2 − x + 2y
у точці М(1, 1, 1).
∂z |
= 2x − 2 y −1; |
∂z |
= −2x + 2 y + 2 |
|||||||||||
∂x |
|
|
|
|||||||||||
|
|
|
|
|
|
∂y |
|
|
|
|
||||
|
∂z |
|
|
= −1; |
|
∂z |
|
= 2; |
||||||
|
|
|
|
|
||||||||||
|
∂x |
|
M |
|
∂y |
|||||||||
|
|
|
|
|
|
|
M |
|||||||
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||
Рівняння дотичної площини: |
|
|
|
|
|
|
|
|
|
|
||||
z −1 = −(x −1) + 2( y −1); |
|
|
x − 2y + z = 0; |
|||||||||||
Рівняння нормалі: |
|
x −1 |
|
y −1 |
|
|
|
|
z −1 |
|
||||
|
|
= |
= |
; |
||||||||||
|
|
−1 |
|
|
||||||||||
|
|
2 |
|
|
|
|
|
|
−1 |
|||||
Наближені обчислення за допомогою повного диференціала.
Хай функція f(x, у) дифференцируема в крапці (х, у). Знайдемо повний приріст цієї функції:
∆z = f (x + ∆x, y + ∆y) − f (x, y) f (x + ∆x, y + ∆y) = f (x, y) + ∆z
Якщо підставити в цю формулу вираз |
|
|
|
|
∆z ≈ dz = ∂f |
∆x + ∂f ∆y |
|
|
|
∂x |
∂y |
|
|
|
то отримаємо наближену формулу: |
|
|
|
|
f (x + ∆x, y + ∆y) ≈ f (x, y) + ∂f (x, y) |
∆x + |
∂f (x, y) |
∆y |
|
|
∂x |
|
∂y |
|
Приклад. Обчислити приблизно значення, |
виходячи |
із значення функції |
||
u = x y + ln z при x = 1, у = 2, z = 1. |
|
|
|
|
Із заданого виразу визначимо x = 1,04 – 1 = 0,04, у = 1,99 – 2 = -0,01, ∆z = 1,02 – 1 = 0,02.
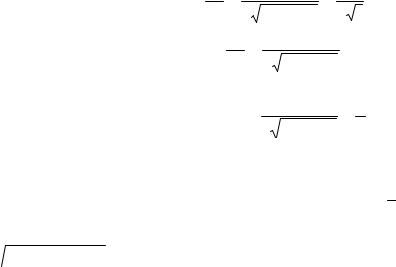
Знайдемо значення функції u(x, у, z)= Знаходимо приватні похідні:
88
|
|
|
|
|
|
|
|
|
“Курс вищої математики. Частина 2.” |
∂u |
= |
|
|
y x y−1 |
2 1 |
=1 |
|||
∂x |
2 |
= |
2 |
1 |
|||||
|
x y + ln z |
|
|||||||
|
∂u |
= |
x y ln x |
= 0 |
|
||||
|
∂y |
|
2 x y + ln z |
|
|||||
|
|
|
|
|
|
|
|||
|
∂u |
|
|
1 |
|
1 |
|
||
|
|
= |
|
z |
= |
|
|||
|
∂z |
|
2 x y + ln z |
2 |
|
||||
du = 0,04 ∂∂ux −0,01 ∂∂uy + 0,02 ∂∂uz =1 0,04 − 0 0,01+ 12 0,02 = 0,04 + 0,01 = 0,05
 1,041,99 + ln1,02 ≈ u(1,2,1) + du =1 + 0,05 =1,05
1,041,99 + ln1,02 ≈ u(1,2,1) + du =1 + 0,05 =1,05
Точне значення цього виразу: 1,049275225687319176.
Приватні похідні вищих порядків.
Якщо функція f(x, у) визначена в деякій області D, то її приватні похідні f x′(x, y) і f y′(x, y) теж будуть визначені в тій же області або її частині.
Називатимемо ці похідні приватними похідними першого порядку.
Похідні цих функцій будуть приватними похідними другого порядку. |
|
|||||||||||||||||||
|
∂2 z |
= |
f xx′′(x, y); |
|
|
∂2 z |
= |
f yy′′ |
(x, y); |
|
|
|
|
|||||||
|
∂x2 |
|
|
∂y 2 |
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
∂2 z |
= |
f xy′′(x, y); |
|
|
∂2 z |
= |
|
f yx′′ (x, y); |
|
|
|
||||||||
|
∂x∂y |
|
|
∂y∂x |
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Продовжуючи диференціювати отриману рівність, отримаємо приватні похідні |
||||||||||||||||||||
вищих порядків. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Визначення. Приватні похідні вигляду |
|
|
∂2 z |
; |
∂2 z |
; |
∂3 z |
; |
∂3 z |
і так далі |
||||||||||
∂x∂y |
∂y∂x |
∂x∂y∂x |
∂x∂y∂y |
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
називаються змішаними похідними. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Теорема. Якщо функція f(x, у) і її приватні похідні |
f x′, f y′, f xy′′, f yx′′ визначені і |
|||||||||||||||||||
безперервні в точці М(х, у) і її околиці, то вірне співвідношення: |
|
|
|
|||||||||||||||||
|
|
|
|
∂2 f |
= |
∂2 f |
|
|
. |
|
|
|
|
|
|
|
|
|
||
|
|
|
|
∂x∂y |
∂y∂x |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
Тобто приватні похідні вищих порядків не залежать від порядку диференціювання.
Аналогічно визначаються диференціали вищих порядків. dz = f x′(x, y)dx + f y′(x, y)
89

“Курс вищої математики. Частина 2.”
d 2 z = d[f x′(x, y)dx + |
f y′(x, y)dy]= f x′′2 (x, y)(dx)2 |
+ 2 f xy′′(x, y)dxdy + |
f y′′2 (x, y)(dy)2 |
||||||||||
d 3 z = |
f ′′3′(x, y)(dx)3 + 3 f ′′2′ |
(x, y)(dx)2 dy |
+ 3 f |
′′′2 (x, y)dx(dy)2 |
+ f |
′′3′ |
(x, y)(dy)3 |
||||||
|
x |
x y |
|
|
|
|
|
|
xy |
|
y |
|
|
|
|
|
|
|
....... |
|
n |
|
|
|
|
||
|
|
|
|
∂ |
|
∂ |
|
|
|
|
|
||
|
|
d n z = |
|
dx + |
|
dy |
|
|
f (x, y) |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
∂x |
|
∂y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Тут n – символічний ступінь похідної, на яку замінюється реальний ступінь після зведення в неї що стоїть з дужках виразу.
Екстремум функції декілька змінних.
Визначення. Якщо для функції z = f(x, у), визначеною в деякій області, в деякій околиці точки М0(х0, у0) вірна нерівність
f (x0 , y0 ) > f (x, y)
то точка М0 називається точкою максимуму.
Визначення. Якщо для функції z = f(x, у), визначеною в деякій області, в деякій околиці точки М0(х0, у0) вірна нерівність
f (x0 , y0 ) < f (x, y)
то точка М0 називається точкою мінімуму.
Теорема. (Необхідні умови екстремуму).
Якщо функція f(x,y) в крапці (х0, у0) має екстремум, то в цій крапці або обидві її приватні похідні першого порядку рівні нулю, або хоч би одна з них не існує.
Цю крапку (х0, у0) називатимемо критичною крапкою.
Теорема. (Достатні умови екстремуму).
Хай в околиці критичної крапки (х0, у0) функція f(x, у) має безперервні приватні
похідні до другого порядку включно. Розглянемо вираз: |
||||||||||
|
|
|
|
|
|
D(x, y) = f x′′2 (x, y) f y′′2 (x, y) −[f xy′′(x, y)]2 |
||||
f ′′2 |
|
|
1) Якщо D(x0, y0)> 0, то в крапці (х0, у0) функція f(x, у) має екстремум, якщо |
|||||||
(x |
0 |
, y |
0 |
) < 0 |
- максимум, якщо f ′′2 (x |
0 |
, y |
0 |
) > 0 - мінімум. |
|
x |
|
|
|
x |
|
|
||||
2)Якщо D(x0, y0)< 0, то в крапці (х0, у0) функція f(x, у) не має екстремуму
Увипадку, якщо D = 0, вивід про наявність екстремуму зробити не можна.
Умовний екстремум.
Умовний екстремум знаходиться, коли змінні х і у, що входять у функцію u = f( x, у), не є незалежними, тобто існує деяке співвідношення
ϕ(х, у) = 0, яке називається рівнянням зв'язку.
Тоді із змінних х і у тільки одна буде незалежною, оскільки інша може бути виражена через неї з рівняння зв'язку.
Тоді u = f(x, у(x)).
dudx = ∂∂fx + ∂∂fy dydx
В точках екстремуму:
du |
= |
∂f |
+ |
∂f dy |
=0 |
(1) |
||
|
|
|
|
|||||
dx |
∂x |
∂y dx |
||||||
|
|
|
|
|||||
90
