
Vakarchuk_I_O_Kvantova_mehanika_Pidruchnik_B
.pdf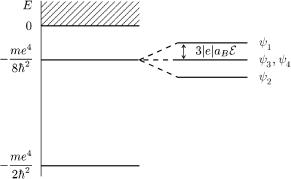
ис 46. озщеплення енер етичних рiвнiв атома водню в електричному |
||||||||||||
ïîëi. |
|
|
|
|
|
|
|
|
|
|
|
|
|
Далi р зглянемо нетривiальнi розв'язки секулярного рiвняння. |
|||||||||||
Перший корiнь |
|
|
|
|
|
|
|
|
|
|
||
З першоготреть та четвертого рiвнянь для |
|
|
|
|||||||||
|
|
E = E1 |
= |V12| = 3|e|aBE. |
|||||||||
ç |
|
рiвняння |
|
|
|
|
|
|
|
Cα ìà¹ìî C3 = 0, C4 = 0, à |
||
|
умови |
|
C1 = |
V12 |
−C2. |
|||||||
Ç |
|
|
E C2 = |
|||||||||
|
нормування знаходèìî явнi вирази: |
|||||||||||
|
|
|
1 |
|
|
|
|
|
1 |
|
||
Îòæå, |
C1 = √ |
|
, |
|
|
|
C2 |
= −√ |
|
. |
||
|
|
|
||||||||||
|
|
|
2 |
|
|
|
|
|
2 |
|
||
|
|
|
|
|
|
|
1 |
|
|
|
|
|
à âiäïîâiäíà åíåð iÿ |
ψ1 = √ |
|
( 1 |
2 ), |
|
|
||||||
|
|
|
||||||||||
|
|
|
|
|
|
|
|
2 | i − | i |
||||
Беремо другий корiньE1 = −me4/8~2 + 3|e|aBE. |
||||||||||||
432 |
E = |
E2 = −|V12| = −3|e|aBE. |
||||||||||

З першого рiвняння
|
C1 |
= |
V12 |
|
|
|
|
|
|
|
|||
|
|
E C2 = C2 |
|
|
|
|
|||||||
i з допомогою умови нормуваííÿ знаходимо |
|
|
|||||||||||
|
|
1 |
|
|
|
|
1 |
|
|
|
|||
|
|
÷èìî, âiäïîâiä๠|
|
|
|
|
|
||||||
C1 |
= i√âiäïîâiäíàC2 |
= |
√ |
. |
|
|
|||||||
Тепер хвильова ункцiя |
|
|
|
|
|
åíåð iÿ: |
|
|
|
||||
|
|
2 |
|
|
|
|
|
|
2 |
|
|
|
|
ах типу бензолу C |
|
àíi÷íèõ π-зв'язках в |
|
||||||||||
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
ψ2 = √2 (|1 + |2 ), |
|
|
|
|
||||||||
46)ÿê. |
|
|
|
4 |
2 |
− 3|e|aBEменше. |
значення енер- |
||||||
Симетричнiйi¨(див.Ÿ 52акож. ункцi¨,рис.E2 |
= áà−me /8~ |
||||||||||||
|
|
спектратрацi¹ютеорiяелектронiвзастосорг ван розв'язалимолекутеорi¨ збурень ¹ |
|||||||||||
розрахунокЩеднi¹юенерπцiкавою-електроннаетичногоiлю |
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
- |
|
|
|
|
|
|
|
|
|
|
|
|
îðèõ.â- |
|
|
|
|
|
|
|
|
|
|
|
|
|
íò |
|
|
|
|
|
|
|
|
|
|
|
|
|
сперимдинармолекуларанiшеявиктим, |
|
|
|
|
|
|
|
|
|
|
посвiдчить.ми47)рiвнiв.'язокiйних.дрiзня¹тьсТобто,Дляекможнаелектроналiнiйних |
|
|||
|
|
|
|
|
|
|
|
÷ó |
|
|
|
|
|
кристщо(дивãàíi÷íèõ.атиутозгалiПриклмиляньмо¹.так¹молекуповнiстюЗрозумiло,суперпозицiйним,àæä¹ìî4äëÿëзамкненийдозамкненийтипурозрахункуиметричною,Ÿ13)щобутадi¹ну.ЗадачаакланцюланцюжокчергуваннянеенерцюдляпрозакрiпленимжокHзадаетичнихщобензолу.(рисˆ¨ |
|
|
|||||||||||
бензолузв'язкiв |
|
|
|
|
|
|
6 6 |
|
|
|
|
|
|
крнимчергуютьссполученiзванимизв'язкоммiж.Кожсобоюатомомзв'язкатомiвдинарнимивовуглецю.Подвiйнавитимутьподвiйнимиожатомамизв'язоксполученийзв'язкамистворенийвугçâ'ÿçêè,öþ,ä- |
|||||
тщоякi |
|
|
|
N |
|
а якихнерелектрониi¨ цих- |
¹- рухливимиами.Нас.Нашецiк завдання самерозрхувати |
||||
ðiâíi |
π |
σ |
|
π |
|
è åëåêò |
îíà íà π-електронiв. Iндексом n будемо нумерувà |
- |
|||
28 I. О. Вакарчук |
n-тому атомi вуглецю. |
|
433 |
||

ис. 47. Молекула бензолу.
Отже, ми знову ма¹мо справу iз секулярною проблемою:
|
X′ |
|
|
− |
|
де матричнi елементи гамiльтонiана зада¹мо так: |
||
|
( Eδnn′ |
+ Hnn′)Cn′ = 0, |
|
n |
|
|
Hnn = E0, |
|
рештак |
Hn,n±1 = −A, |
|
|
|
- |
електронадiв,вузлиолиою,виглядi.враховуюункцi¹юIмщосильновдорiвню¹рнрiвнянняслокЦенаступнихòüсяалiзована¹перехнулевiстрибкиакдлязванедусусiдiв.кIоенаелêøåвузлiнаближенняiцi¹нтiвлектрона.Урахжучи,неовуючичерезперекрива¹тьслишехвильованайближчихвузолце,першiвипишемоуважа¹тьункцiязсусухвисiд |
||
льовоюявномус Hnn′ |
= 0. |
|
|
|
|
|
|
|
|
|
Cn: |
|
àáî |
(E0 − E)Cn − ACn+1 − ACn−1 = 0 |
||||||||
434 |
C |
n+1 |
= |
E0 − E |
C |
n − |
C |
n−1 |
. |
|
|
|
A |
|
|
||||
|
Запишемо це рiвняння в компактнiшiй ормi. Для цього вве- |
|||||||||||||||
демо вектор |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
та так звану транс ер- |
|
Xn |
= |
|
Cn |
|
|
|
|
|
||||||
|
|
|
матрицю |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
Cn−1 |
|
|
|
|
|
|||
|
|
êîåT = |
E0−E |
− |
1 |
. |
|
|
|
|||||||
Тепер рiвняння для ˆ |
iöi¹íòiâ |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
A |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Cn запишемо так: |
|
|||||||
|
Оскiльки ланцюжок |
замк ений,електроноеˆ òî |
iöi¹íò |
|
||||||||||||
|
Xn+1 = T Xn. |
|
|
|
|
|
|
|||||||||
збiгатись iз кое iцi¹нтом |
|
|
|
|
|
|
|
|
|
|
CN +1 повинен |
|||||
|
|
граничних, кое iцi¹нт |
CN +2 ç ê å iöi¹íòîì |
|||||||||||||
|
|
|
|
C1 |
|
|
|
|
|
|
||||||
àòîìiдор вню¹ ймовiрностi того, що |
|
|
|
|
знах диться на |
2 |
||||||||||
C2 |
.д. Нагада¹мо, що, згiдно з принципом суперпîçèöi¨, |Cn| |
|||||||||||||||
|
вуглецю. Iз цих |
|
|
|
|
|
умов виплива¹, що |
n-òîìó |
||||||||
Лiву частину цi¹¨ |
|
|
можна записати ще й так: |
|
||||||||||||
|
|
рiвностi XN +2 |
= X2. |
|
|
|
|
|
|
|||||||
|
отримали однорiднеˆ |
ëiíiéíåˆ ˆ |
рiвнянняˆ для вектора |
|||||||||||||
Îòæå, ìè XN +2 = T XN +1 = T T XN = . . . = T |
N |
X2. |
|
|||||||||||||
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
X2 |
àáî |
|
|
|
ˆN |
X2 |
= X2, |
|
|
|
|
|
|
||||
|
|
|
T |
|
|
|
|
|
|
|
||||||
|
|
|
|
ˆNрозв'язку цього |
|
|
|
|||||||||
|
Умовою нетривiального(T |
− 1)X2 |
= 0. |
|
рiвняння ¹ |
|
||||||||||
28* |
|
|
|
ˆN |
− 1| = 0. |
|
|
|
|
|
435 |
|||||
|
|
|
|T |
|
|
|
|
|
|
|||||||

З нього знаходимо ен р етичнi рiв |
i електрона. Використа¹мо тео- |
||
ðåìó € óññà ïðî êîðåíi àë |
ебра¨чного |
рiвняння i запишемо таке |
|
матричне рiвняння: |
|
|
àäà¹ìî, |
де величини e |
N −1 |
|
|
Y |
Tˆ − e2π s/N |
TˆN − 1 = s=0 |
нант добутку матриць2πis/N ¹ коренямидорiвню¹здîдиницiбутковi. Нагдетермiнантiвщоматриць:детермi-
Тепер рiвняння для|T |
|
− 1| = s=0 |
T − e |
|
|
. |
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
Y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆвизначення рiвнiвˆ енер i¨ зводиться до такого: |
|||||||||||||||||||
|
|
|
|
N |
|
|
|
|
|
N −1 |
|
|
|
|
|
|
2πis/N |
|
|
|||
|
|
|
|
|
|
|
T − e |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
= 0. |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ˆ, ìà¹ìî |
||||
Використовуючи явний виглядˆ |
матрицi |
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2πis/N |
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
T |
|
|
|
||||
|
|
E0−E |
|
1 |
e2πis/N |
|
|
|
e |
1 |
|
|
|
|||||||||
|
|
|
A |
|
|
− |
|
|
|
|
|
− |
|
− |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2πis/N |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
= 0, |
||||||||
− |
|
E0 |
A |
|
E |
− |
2πis/N |
|
2πis/N |
|
|
|
||||||||||
|
|
|
− |
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
e |
|
|
|
|
e |
|
|
|
+ 1 = 0, |
|||||
|
|
ðiâíiA− |
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
− e |
|
|
|
= e− |
|
|
|
. |
||||||||||
Отже, дозволенi |
|
E0 |
|
|
E |
|
|
|
|
|
|
|
|
|
|
2πis/N |
|
|||||
|
|
|
åíåð i¨ 2πis/N |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
Es = E0 − 2A cos |
|
2πs |
, |
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
N |
|
|
|||||||||||||||
i¨ Цiкаво порiвняти нашs =результат0, 1, . . . , Niç −îðìó1. ëîþ äëÿ ðiâíiâ åíåð
кулярногорималиπ-електронаПрикладiрiвняння:лiнiйному4доŸ13незапряìимкненр зрахункла цюомжку,визначникаякуми отсе-
436 |
Es = E0 − 2A cos |
πs |
, |
|
|||
N + 1 |
випадкуЦейрезультатперiодично¨можнаструктуриsодержати= 1, 2рiвняння, . . .é, Niíøèì. дляшляхомкоеiцi¹нтiв.Справдi, у
Cn
можна задовольнити пiдстановкою |
|
= 0 |
|||
|
(E0 − E)Cn − ACn+1 − ACn−1 |
||||
звiдкирезу |
атi отримати |
iαn |
, |
n = 1, 2, . . . |
|
Cn e |
|
||||
(E0 − E) − Aeiα − Ae−iα = 0,
Êóò |
E = E0 − 2A cos α. |
|
α визнача¹мо з граничних умов |
|
C0 = 0, |
якiомбiнацiюнеланцюжкдопускрозв'язкiвають.Цiмоумовижливостiiздодатноюзадовжами перебуванняльняютьсвiд'¹мною,електронаякщовзятиазами,позалiнiйнуме- |
|||||
|
CN +1 = 0, |
|
|
|
|
|
|
|
|
|
Cn |
sin αn. Перша умова задов льня¹тьс |
òðèâià ü î, |
äðóã ä๠|
|||
|
|
|
ланцюшеаспарнiжкiвдовиписаногоармонiки¹ ñóòò¹â |
||
|
що й приводитьма¹моаклад |
|
|
||
|
незамкненогой, |
|
|
|
|
αрiзнимивище(N +озв'язкирезультату1). =Äëÿπs,длязамкненогоs .= 1 2, . . .ланцюжк, N |
повний |
ÿä |
|
||
(0, 2π/N , 4π/N, . . . , äëÿ |
|
|
|||
нвплива¹Ÿ5(поблизуπ/ровестиу,ндричнаегкi í(àêöi¨Nакобговореннiрозрiзня¹мо+.йзакнепарТут1)аналогiюрезо,2итогоуба,дляπ/àíñ(Nнаочно¨якармонiкиграничнихзвучанняпорожниниêiíöÿ)+дерев'яними1)поводить,3iлюстрацi¨якπ/. Ì(óìîâ,Nлейтиiдкритжротасебе+iíøмузичними1)ùîâðiç,а(внаслiдок.кларнетм,.онавця.èöi)обох.Мицихêiiнструмент.вжютьс.нцiвстьКларнетрозв'язкiвФлейтвеликогозвукузупинялисьма¹нахвильовiами:якотворуцелейтиакпаржнацимиж- 437
ц лiндрична |
|
àëå |
дним закритим кiнцем, |
éîãî çâóê ì๠|
|||||
чаннюèõ ã |
|
еттруба,свî¹р дно¨ мелодiйностi . Правда, пропуски пар |
|||||||
|
|
властивструментiвзбiльшують |
|
мiж модамиармонiк |
|
òîìó |
|||
не виник |
|
групи гобоя (гобой, англiйський |
|||||||
øå íåï |
|
|
г рм нiки. В дсутнiсть парних г |
|
íàä๠çâó |
||||
для кларнет |
|
|
тервал |
виконання. Цi трудно- |
|||||
ð æîê, à |
ають, онтра а от),äíîùiÿê |
¹ |
iчними трубами, |
îòæå, ç |
|||||
повнимармонiкядом |
армонiк, |
як цилiндричтехнiцiа труба, що вiдкритоливань,з обох |
|||||||
ùiê íöiâ. |
|
|
|
|
|
|
|
|
åíåð- |
Для прикладу розглянемо молекулу бензолу. Випише |
|||||||||
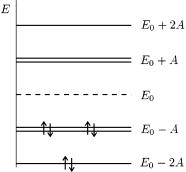
рисетичнi.48. рiвнi замкненого ланцюжка для N = 6 i зобразиìî ¨õ íà
èñ. 48. Åí |
|
етичнi рiвнi бензольного кiльця. |
|||||
Пiдраху¹мо |
вну енер iю основного стану, пам'ятаючи, що а |
||||||
напрямленими |
спiнами,знахтакож ураховуючи, що другий рiвåíü ¹ |
||||||
жному рiвнi |
îæóòü |
|
|
одитись два електрони з протил жíî |
|||
двократно виродженим: |
|
|
|
|
|
||
У розрахункуE = 2(E0 |
− 2A) + 4(E0 − A) = 6E0 − 8A. |
||||||
на один електрон ця енер iя |
|||||||
|
|
|
|
E |
4 |
|
|
438 |
|
|
|
|
= E0 − |
|
A |
|
|
|
N |
3 |
|||
i вонасистемаменша,¹ йнинiæчоюу випадкунезалежнимидля мок ëèвихмолекулакiльцевихбензолузв'язкмолерозгляда¹тьсу . До речi,ÿ
з трьома подвiйними ам енер
ïëàÿêвонадрахуватио¨бензолувсьомуE/N =кiльцю,¹повнуEнайстiйкiшою− Aтоенер.Тмолекулаобто,. вУякщозагцьста¹альномуелектронамстабiльнiшоюневажквипадкуперекдозв.дляОтже,îнатись,лит молекубiгатиякщо
0
iâ: |
|
|
|
|
|
|
|
|
|
|
|
|
|
N електро- |
результат:ша¹мономупричомурiвнiчитпiдсумовува¹E = X (E0 |
− 2A cos (2πs/N )) , |
- |
||||||||||||
|
чевi цейелектрони,простий,необхiдноа алечастиназцiкавийурахуваннямрiвнiврозрахуноквиродженiтого,.щоНаведемона.Заликж |
|||||||||||||
N ó |
|
|
|
|
|
|
çрозумiло, |
|
|
|
||||
|
|
N E0 |
− 2A cos2 |
|
π |
/ sin |
π |
, N − непарне, |
||||||
|
2N |
2N |
||||||||||||
|
|
|
− |
|
|
|
N |
|
|
|
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Число |
|
N E0 |
− 4A |
tg Nπ , |
|
|
|
N/2 − |
. |
|||||
|
|
|
|
|||||||||||
E = |
|
N E0 |
|
4A |
sin |
π |
|
|
|
N/2 |
|
непарне, |
||
|
|
|
випадку, |
|
|
|
|
|
¹ парним. Величина |
|||||
|
нашому |
|
|
|
|
|
||||||||
äåëü, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ε = E − N E0 |
|
|
|
|||||||
як ункцiя числа |
|
|
|
|
|
|
4AN |
|
|
|
||||
|
|
N зображена |
а рис. 49. Вона досяга¹ мiнiмуму |
|||||||||||
молекудi реТàкимлiзунайсаме¹тьсчином,якутiйкiшiпримолсåредкулатi молеку.бензолуУжливихграли,ицi.Цiкаво,кiльцевихдляякихщома¹мосередмолекулвiртуприрольних.- |
|||||
ε = −1/3 |
N = 6 |
|
N → ∞ |
ε = −1/π |
|
|
|
|
N/2 |
¹ |
непарним, |
|
|
|
|
|
- |
|
|
|
|
|
à, |
якихМольногознрозрахунзв'яздяться. миêó)розглянули,йони,.електронногоПозначимочерезвузлпрямоспектрадальстосу¹ться,мiжкристалавузламияк(наближужлацюзазнаенк |
|||||
NБунячалось,= 10 14, . . . |
|
|
|
|
|
äåìî ââ æàòè, ùî êiëüêiñòü |
a;iдовжина¹ великою,ланцюжк |
L = N a. |
|||
хвильовий вектор |
k: |
|
N → ∞. Уведемо |
||
|
|
|
|
|
|
|
k = |
2πs |
, |
|
439 |
|
|
|
|||
|
|
L |
|
|
|
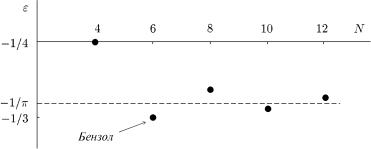
ис. 49. Залежнiсть енер i¨ замкненого ланцюжка вiд кiлькостi вузлiв |
||||||||
у розрахунку на один атом. |
|
|
|
|
|
|
||
Тквазiнеперервнимирiвнiенерi¨ |
|
2πs |
= |
|
2πs |
a = ka. |
||
|
|
|
||||||
|
|
N |
|
L |
||||
¹ |
E = E0 − 2A cos ka |
|||||||
|
(Δk = 2π/L → 0) i утво юють зону шириною |
|||||||
4A. При малих значеннях хвильового вектора |
||||||||
äå m = ~2/2Aa2 |
ективна маса åëåêòðîíà, а величина (E0 − |
|||||||
й енер iя електрона як ункцiя хвильового вектора |
||||||||
|
|
|
|
1 |
(ka)2 + . . . |
|||
E = E0 − 2A 1 − |
2 |
|||||||
частинковий вигляд: |
|
|
|
|
|
|
|
k ì๠âiëüíî- |
|
E = E0 |
|
|
|
|
~2k2 |
||
|
− 2A + 2m |
|||||||
|
|
|
|
|
|
|
|
|
440Шредин2i¨A)i визнача¹назива¹тьсозглянемоера, положякийщеварiацiйнимŸо53åдинруння. ту¹тьсяВарiацiйнийпiдхiдднаенерметодомнаближетично¨принципiпринцип. еногоЦейзониметодмiнiмальностiрозв'язку.працю¹рiвнянняенерпри-
|
задач, для яких ст дартна |
збурень не за- |
|
стосовна. Деякою мiрою успiх варiацiйного теорiяпiдх ду залежить вiд |
|||
iнту¨цi¨ т досвiду. Ми вж мали з ним справу ранiше в декiлькох |
|||
озглянемо |
квантовомеханiчну систему, що характеризу¹ться |
||
дачах. |
|
|
|
ìiëüò íiàíîì |
ˆ |
|
|
розв'язуваннiг |
|
|
|
ò êó, ù á |
|
H. Виберемо деяку пiдхожу ункцiю, ψ = ψ(q), |
|
Z
||2
i пiдраху¹мо з нею середн¹ значенняψ dq = 1,
|
|
âàðiàöiéíó |
|
|
|
ˆ |
|
hH |
|||
|
|
|
|
|
H: |
|
|||||
Цюни ункцiю називаютьhH = Z |
|
|
|
|
|||||||
ψ Hψ dq. |
|
|
|||||||||
|
|
|
пробноюˆ |
. Будемоˆ |
вимаг ти, щоб малi змi- |
||||||
дковурàтковнжаумову. Пiдраху¹моюмовоюжнанормуваннязняти,варiацiюяк âiäîìî,на хвильовууведеннямункцiюмноæíèêiâ. Цю додзЛдоàò- |
|||||||||||
|
|
|
|
|
|
|
ˆ |
|
|
|
|
âàðiàöiÿψ не змiнювали середнього hH . Тобто при зàìiíi ψ íà ψ + δψ |
|||||||||||
|
âàðiàöiþ |
|
|
ˆ |
|
|
|
|
|
||
Ми с рмулю али |
|
|
δhHзадачу= 0. для ункцiо ала |
||||||||
|
|
|
|
|
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
ˆ |
|
|
|
|
|
|
|
|
|
|
hHi: |
|
|
|
|||
Âiäíiìåìî âiä |
ˆ |
|
|
умовиˆ |
нормування,ˆ |
|
|||||
|
íå¨δhH |
|
= Z δψ Hψ dq + Z ψ Hδψ dq. |
|
|||||||
|
δ Z ψ ψ dq = Z |
Лаδψ ранжаψ dq + Z |
ψ δψ dq, |
|
|||||||
помноживши ¨¨ на множник |
|
|
|
|
|
|
|
||||
на безумовний екстремум: |
|
|
|
|
|
E, i отрима¹мо рiвняння |
|||||
Уважаючиˆ |
− E Z |
δψ ψ dq + Z |
ˆ |
|
ψ δψ dq = 0. |
||||||
Z δψ Hψ dq |
ψ Hδψ dq − E Z |
||||||||||
нiмум середнього значенняезалежними,гамiльтонiана:з ходимо двi умови на мi- |
||
δψ i δψ |
|
|
Z |
δψ (Hψˆ − Eψ) dq = 0, |
441 |
