Работа 3

Работа 3

ИССЛЕДОВАНИЕ МНОГОКАНАЛЬНОЙ СИСТЕМЫ ПЕРЕДАЧИ ИНФОРМАЦИИ С НЕЛИНЕЙНЫМ УПЛОТНЕНИЕМ КАНАЛОВ

Цель работы - изучение нелинейного метода уплотнения кана­лов и способа разделения каналов по форме сигналов.

Общие сведения

Многоканальные системы предназначены для передачи по одному радиотракту сообщений от нескольких источников информации. Сообщения каждого источника модулируют выделенный данному ис­точнику сигнал, который называют также переносчиком или поднесущим колебанием.

Модулированные канальные сигналы объединяются по некоторо­му правилу в групповой сигнал, который модулирует несущее ко­лебание. Модулированная несущая поступает в высокочастотный тракт. Операцию получения группового сигнала из канальных на­зывают уплотнением каналов.

На приемной стороне осуществляются обратные операции: вы­деление группового сигнала и сигналов отдельных каналов. Полу­чение канальных сигналов из группового называется разделением каналов. Переданные сообщения выделяются при демодуляции ка­нальных сигналов. В некоторых случаях операции разделения и демодуляции выполняются одним устройством одновременно.

Разделение каналов производится в присутствии помех как внешних (внесистемных), так и внутренних (внутрисистемных). Природа и действие внешних помех такие же, как и в одноканальных системах. Внутренние помехи являются существенной особен­ностью многоканальных систем передачи информации. Появление внутрисистемных помех обусловлено тем, что по одному радиотракту передается совокупность канальных сигналов. В этом случае для любого канала сигналы других каналов представляют собой помеху.

Отличие внутрисистемных помех от внешних состоит в том, что их влияние на качество разделения определяется свойствами канальных сигналов, которые выбираются разработчиком системы.

Поэтому основная задача при построении многоканальных систем состоит в выборе такой совокупности канальных сигналов и та­кого метода их обработки, которые обеспечивают разделение каналов без взаимных помех.

Существуют линейные и нелинейные методы уплотнения и раз­деления каналов. При линейном уплотнении групповой сигнал получается как линейная комбинация канальных сигналов. Линейное разделение каналов предполагает обработку группового си­гнала линейными устройствами.

Выбор к ан а л ь н ы х сигналов. Доказано, что при линейном уплотнении и разделении каналов внутрен­ние помехи не влияют на разделение, если канальные сигналы составляют ансамбль линейно независимых или ортогональных сигна­лов. Сигналы у;(t) ортогональны на интервале (О,Т) ,

Наиболее распространенные ансамбли ортогональных сигналов -это последовательности неперекрывающихся по времени импульсов и сигналы с неперекрывающимися частотными спектрами. Использоваие в качестве поднесущих импульсных последовательностей приводит к системам с временным разделением каналов (ВРК), использование сигналов с неперекрывающимися спектрами - к сис­темам с частотным разделением каналов (ЧРК).

Однако ортогональность сигналов может быть обеспечена не только при несовпадении их во времени иди по спектру, но и за счет особой формы сигналов. Например, полиномы Чебышева, Ла- герра ,Эрмита, функции Уолша, Хаара и т.п, образуют ортого-­ нальные системы функций и, следовательно, могут составлять ан-­ самбли канальных сигналов. Использование ансамблей ортогональ-­ ных функций приводит к системам с разделением каналов по фор- ме.

Главным фактором при выборе ансамблей ортогональных сиг­налов является простота технической реализации аппаратуры уп­лотнения и разделения каналов. Широкое применение цифровых

устройств в многоканальных системах возможно при использо­вании дискретных ортогональных и квазиортогональных сигналов (импульсно-временных кодов, функций Уолша, Хаара, псевдослучай­ных последовательностей).

В лабораторной работе изучается многоканальная система с использованием в качестве канальных сигналов функций Уолша. Функции Уолша особенно удобны при использовании цифровых устройств, так как принимают всего два значения +1 и -1.

Функции Уолша задаются на дискретном интервале (0, W -1), причем n=2^K , где k= 1,2,3... . Если рассматри­вать функции Уолша как двоичные кодовые слова, то n - чис­ло символов в слове. Из n различных функций Уолша можно со­ставить много систем ортогональных функций, отличающихся спо­собом упорядочения (нумерацией) функций.

Для практического генерирования функций Уолша наиболее важна система упорядочения Уолша-Пэли. В этой системе все функции выражаются через функции Радемахера, которые легко формируются с помощью многоразрядного двоичного счетчика.

Функции Радемахера определяются соотношением

Функции Радемахера имеют вид правильной прямоугольной кривой - меандра, поэтому их называют иногда меандровыми функциями. На рис.3,1 показана система функций Радемахера для n= 8. Следует обратить внимание на совпадение функций Радемахера и.временных диаграмм, иллюстрирующих работу трех­разрядного двоичного счетчика.

Функции Уолша W_m (Θ) , упорядоченные по Пэли, получа­ются перемножением функций Радемахера:

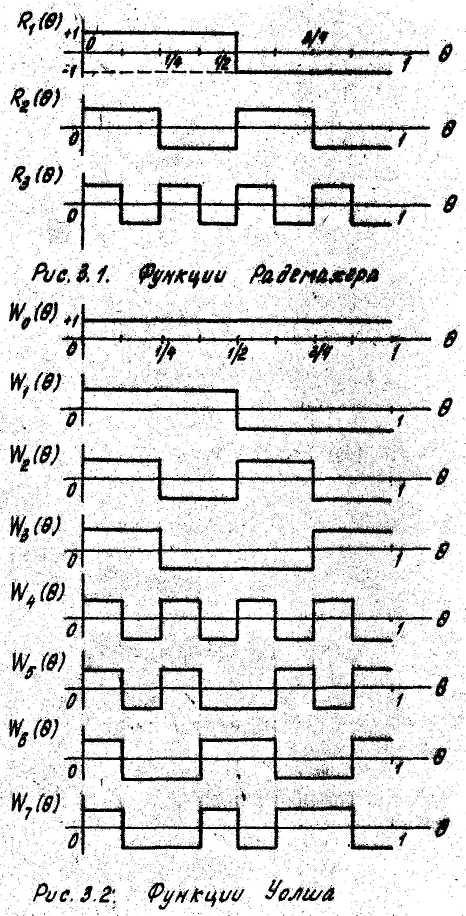
Для K=3 (n= 8) система Уолша-Пэли содержит следующие функции(рис.3.2)

Система кусочно-постоянных функций Уолша является полной орто­гональной системой.

Представление функций Уолша в виде (3.2) определяет простой способ их генерирования. Если сопоставить значению функ­ции Уолша, равному 1, логический нуль, а значению функции Уолша, равному -1, логическую единицу, то операции умножения функций Радемахера будет соответствовать сложение по тоd2.

Поэтому функцию Уолша (3.2) можно представить как пере- ключательную

Таким образом, функции Уолша могут формироваться устрой­ством, состоящим из двоичного счетчика для получения функций Радемахера,и комбинационной схемы, реализующей переключатель-ную функцию (3.3).

Канальные сигналы Yi(t) в многоканальных системах полу­чаются модулированием поднесущих Ai(t) . При использовании в качестве поднесущих функций Уолша возможна модуляция по амплитуде, по частоте следования (кодовая модуляция), по временному положению и временной базе. Однако ортогональность канальных сигналов и, следовательно, разделение их без взаим­ных помех можно обеспечить только при амплитудной и кодовой модуляции. Эти виды модуляции и могут быть использованы в

многоканальных системах.

Наиболее просто осуществляется амплитудная модуляция, при которой модулирующий сигнал Xj перемножается с функ-­ цией Уолша , Yj=Xj*Aj(t) , где Aj (t) функция Уолша, поднесущая у канала.

В случае представления сообщения двоичной последователь- ностью символов Хj = (хj1, Хj2,..., Хji) значение

каждого символа xji умножается на функцию Уолша, и

канальный сигнал состоит из l кодовых комбинаций значности n , передаваемых последовательно. Поэтому в дальнейшем рас­сматривается передача одного входного символа Xj по каждому из N каналов.

Таким образом, в многоканальной системе, использующей функции Уолша в качестве поднесущих и предназначенной для пе­редачи дискретных сообщений, модулированный канальный сигнал или совпадает с кодовой комбинацией, соответствующей функции Уолша: Yj(t) = Aj(t), или противоположен ей; Yj(t)=-Aj(t)

У п л о т н е н и е к а н а л о в .Групповой сигнал У_гр можно получить из канальных как линейными, так и нели­нейными способами. Простейший способ линейного уплотнения состоит в алгебраическом сложении канальных сигналов:

где N - число уплотняемых каналов.

Групповой сигнал при этом получается многоуровневым, что затрудняет реализацию приемо-передающей аппаратуры.

Определение знака суммы Yj равносильно операции мажоритар-

Двухуровневый групповой сигнал с минимальным пик-фактором получается в случае нелинейного уплотнения. Один из способов заключается в том, что значение группового сигнала оп­ределяется знаком алгебраической суммы канальных сигналов:

Групповой сигнал Y_грм(t) , описываемый кусочнопосто-янной функцией (3.4), может быть представлен конечным рядом

ности, проводимой над одноименными разрядами кодовых комби- наций Yj , j= Поэтому такой способ уплотнения кана­лов называется мажоритарным.

В соответствии с операцией мажоритарности значение i -го символа группового сигнала y_j= +1, если большинство i- х символов канальных сигналов равно +1, и y_i= -1, если больши­нство i- г символов канальных сигналов равно -1 (число кана­лов предполагается нечетным).

Р а з д е л е н и е к а н а л о в и д е к о д и- р о в а н и е с и м в о л о в. Операции разделения и де­- кодирования осуществляются в каждом канале путем вычисления коэффициента корреляции r_j между принятым групповым сиг-­ налом и опорным, соответствующим функции Уолша данного кана­- ла:

Для вынесения решения о значении переданного символа rj сравнивается c порогом.

При линейном уплотнении ортогональных канальных сигналов вычисление коэффициента, корреляции является достаточным для разделения и декодирования без взаимных помех. Действительно, коэффициент корреляции в j - м канале можно представить в виде

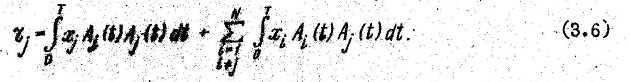
Второе слагаемое в выражении (З.6) равно 0 в силу ортого- нальности функций Уолша. Поэтому r_j=cx_j , где С =

, если A j(t) , j= являются n-значными ортогональными кодовыми комбинациями. Видно, что коэффициент корреляции r_j определяется значением переданно­го символа xj=±1 и не зависит от значений символов, пе­редаваемых по соседним каналам (междуканальных искажении нет).

Покажем, что и при нелинейном, мажоритарном уплотнении возможно разделение каналов без взаимных помех.

где _i - постоянные коэффициенты.

Первая сумма в этом ряду пропорциональна групповому сигна­лу при линейном уплотнении. Подставляя (3.7) в выражение (3.5} о учетом (3,6) получим

где z_i l=- коэффициент корреляции l суммы в разложении (3.7) и функции Уолша Аj(t) .

Коэффициенты z_l зависят от значений символов, передавае­мых по соседним каналам, и от ансамбля поднесущих, функций Уол­ша. Для полного устранения междуканальных помех требуется, что­бы Z_e = 0 для всех l= и всех j =.

Известно, что произведение функций Уолша есть функция Уол­ша с другим номером

где mn – обозначение поразрядного сложения по mod2 двоичных представлений чисел m и n

C учетом этого свойства и свойства ортогональности, можно заключить, что z_l= 0 для всех , l= , если поразрядная сумма номеров перемножаемых функций Уолша в (3.7) не совпадает с номером функции Уолша, поднесущей j канала. Очевидно, что чем больше функций Уолша в ансамбле, из которого выбирается N поднесущих, то есть чем больше значность п кодовых ком- бинаций Аi(t) , тем легче выполнить это ycловие. Доказано, что междуканальные помехи отсутствуют при мажоритарном уплот­нении, если n≥2^N-1 . Тогда коэффициент корреляции в j - м канале

В случае, если n< 2^N-1 , возникают междуканальные помехи, уровень которых определяется структурой ко­довых комбинаций А_i .

Оценка X_j^* переданного символа X_j^* в каждом канале производится по правилу

X_j^*=sign r_j , j= (3.9)

Выражение (3.9) означает, что если коэффициент корреля­ции r_j положителен, то принимается решение x_j^* = 1,если r_j отрицателен, то х_j* = -1.

В отсутствии внешних помех алгоритм (3.9) обеспечивает правильное решение при сколь угодно малой величине коэффици­ента корреляции, что является следствием разделения каналов без взаимных помех. При наличии помех, искажающих групповой сигнал, оценка по знаку коэффициента корреляции приводит как и правильным, так и к ошибочным решениям.

Вероятность ошибочного декодирования символа Xj уменьша­ется с увеличением r_j , Так как абсолютная величина коэф­фициента корреляции при мажоритарном уплотнении меньше, чем при линейном (₁ <1 ), то мажоритарный способ уплотнения уступает по помехоустойчивости линейному. Проигрыш обусловлен тем, что при N канальной корреляционной обработке группово­го сигнала учитываются только N первых членов разложения (3.7).

Корректирующая способность канальных сигналов при мажоритарном уплотнении. Установим связь между искажениями группового сигнала и ошибками в приеме символа x_j , j = . Искажения группового сигнала У_гр будем оценивать кратностью ошибки , q - числом искаженных симво­лов в принятой комбинации У_гр , а корректирующую способность кратностью исправленных ошибок q_испp

Задача обнаружения ошибок в групповом сигнале решается путем сравнения полученного коэффициента корреляции r_j и коэффициента r_j0 , вычисленного по (3.8) при отсутствии искажений. Ошибки могут быть обнаружены, если r_j ≠ r_j0,.

и не могут быть обнаружены, если при наличии искажений r_j = r_j0

Исправление ошибок связано с правилом оценки переданного символа (3.9). При этой любая ошибка исправляется, то есть в присутствии искажений принимается правильное решение о зна­чении символа X: , если знак коэффициента корреляции не изменяется

sign r_j = sign r_j0 . Ошибка не исправляется, если искажения приведут к изменению знака коэффициента корреляции sign r_j = -sign r_j0 .

Коэффициент корреляции между кодовыми комбинациями

A_j = (a_j1, a_j2,...,a_jn) и

Yгр = (y₁,y₂,…,y_n)

можно представить в виде

где a_ji = ±1 и y_i = ±1 •

Из выражения (3.10) следует, что величина коэффициента r_j0 определяется числом позиций, на которых совпадает n_совп и . отличаются n_несовп символы кодовых комбинаций А_j и Y_гр:

причем n_совп + n_несовп = п

Коэффициент корреляции можно выразить через расстояние между комбинациями А_j и У_гр . По определению расстояние d_j равно числу позиций, в которых отличаются две кодовые комбинации

-d_j =n_несовп

Поэтому

Выражение (З.12) показывает, что если расстояние d_j изменяется на 1, например, вследствие однократной ошибки, то коэффи­циент корреляции изменяется на 2.

В соответствии с (З.11) величина коэффициента корреляции, а следовательно, и вероятность неправильной оценки x_j , зависит не только от кратности ошибки, но и от распределения общего числа исправлений по множествам позиций n_совп, и

n_несовп, Кроме того, при передаче Xj =+1 наибольший вред причиняет ошибка, исказившая символы на позициях из множества n_совп , а при передаче Xj = -I - ошибка, исказившая символы на позициях из множества n_несовп Таким образом, влияние искажений группового сигнала на оценку передаваемых символов определяется многими факторами, что затрудняет анализ корректирующей способности применяемых сигналов.

Рассмотрим случай x_j = +1, когда для правильного приема необходимо, чтобы r_j>0 . Тогда можно выделить три вида искажений группового сигнала У_гр :

• искаженные символы находятся на позициях, в которых Аj совпадает о Y_гр (при Xj = +1 худший случай);

• искаженные символы находятся на позициях, в которых А_j отличается от Y_гр (лучший случай);

• часть искаженных символов q_совп расположены на позиции-­ ях, в которых A_j совпадает с Y_гp , часть q_несовп - на

позициях, в которых А_j отличается от Y_гр ( q_совп + q_несовп=q)

В худшем случае ошибка кратности q уменьшает коэффици­ент корреляции на 2q единиц. Но решение о переданном симво­ле будет правильным, если знак коэффициента остается положи­тельным (Xj = +l). Поэтому кратность исправляемых ошибок в любых сочетаниях q_испр (r_j0 -1)/2

Во втором случае ошибка кратности q увеличивает r_j на 2q единиц и, следовательно, исправляются все сочетания ошибок q_ucnp. n_несовп .

Третий случай является промежуточным: влияние ошибки кратности q эквивалентно ошибке кратности q_экв = /q_совп - q_несовп/ причем, если q_совп > q_несовп , коэффициент корреляции уменьшается на 2q_зкв единиц, если q_совп < q_несовп , коэффициент r_j увеличивается на 2q_зкв единиц.

При q_совп < q_несовп r_j = r_j0 что соответствуeт отсутствию искажений группового сигнала.

Аналогичные рассуждения можно провести для случая передачи x_j = -1. Следует только отметить, что групповой сигнал от­личается и совпадает с канальными сигналами на разных позици­ях для разных каналов и X, = ± 1. Поэтому один и тот же вид искажения группового сигнала будет неодинаково влиять на пра-

вильность приема x_j , j=1, N : в некоторых каналах ошибка будет исправлена, в других - нет. Однако при любых условиях будут исправлены ошибки, кратность которых опреде­лена для худшего случая -

Пример. Рассмотрим работу трехканальной системы передачи информации с мажоритарным способом уплотнения и раз-делением каналов по форме сигналов.

Упрощенная схема системы приведена на рис.3.3. На схеме формирователи функций Уолша обозначены как генераторы адре­сов А₁ , А_г и A₃ . Этим подчеркнуто, что вид функций Уолша, используемых в качестве поднесущих, определяет также и номер (адрес) канала.

Каждый из 3 источников данных формирует сообщения, пред­ставленные комбинациями двоичных символов Xj . При обозна­чении символов в виде 0 и 1 модулированные канальные сигналы Yj представляют собой n -значные кодовые комбинации, совпадающие или с прямой, или инверсной комбинацией адреса Аj . Прямое слово, .

a_ji = 0; 1 совпадает с двоичной последовательностью, полученной из функции Уолша при замене -1 на 1 и +1 на 0. Канальный сиг­нал Yj = Aj формируется, если требуется передать xj =0.

Инверсное слово

получается из прямого заменой всех единиц на нули, а нулей на еди­ницы. Канальный сигнал Уj = формируется при передаче

хj = 1

Канальные сигналы снимаются с выходов сумматоров по mod2,

а групповой сигнал Y_гр - с выхода мажоритарного элемента. В передатчике ПРД групповой сигнал модулирует несущую и излучает-­ ся в пространство. Формирование группового сигнала Y_гр при мажоритарном уп­- лотнении трех каналов иллюстрируется временными диаграммами на рис.3.4. Диаграммы построены для случая, когда по первому кана- лу передается сообщение, закодированное последовательностью 1 0 1, по второму - последовательностью 1 1 1, по третьему - 1 0 0. В качестве адресов выбраны функции Уолша A₁ = W₀₁₀ ,

A₂ = W₀₁₁ , A₃ = W₁₀₀

На приемной стороне сначала выделяется групповой сигнал Y'_гp , а затем с помощью корреляторов и пороговых элементов

ПЭ принимается решение о значении переданного символа по каждому каналу.

Коррелятор выполнен в виде последовательного соединения умножителя и интегратора умножитель поступают двоичные n - значные кодовые комбинации, соответствующие принятому групповому сигналу Y'_гр и адресу данного канала Aj .Поразряд­ное умножение двоичных комбинаций с символами +1,-1 эквивалентно суммированию по mod2 символов 0 и 1.Интегратор обеспечивает суммирование результатов перемножения за время Т, равное длительности передаваемого символа Xj, j=1,2,3.

Оценка значений переданных символов x^*_j производится по­роговыми элементами в соответствии с алгоритмом (3.9) и пра­вилом формирования канальных сигналов на передающей стороне.

Система синхронизации условно показана состоящей из двух блоков: блока синхросигналов на передающей стороне и блока выделения синхросигналов на приемной. Блок синхросигналов обеспечивает формирование ортогональных адресов A₁ , А_г , A_s и сигнала синхронизации, передаваемого по каналу связи. В прием­нике выделенные синхросигналы используются для получения ко­дов A₁ , А₂ , А₃ .начало и моменты смены символов в которых совпадают с соответствующими моментами принятого группового сигнала Y'_гр .Сброс интеграторов также осуществляется выделенным синхросигналом.

Процесс разделения каналов и декодирования символов поясняется временными диаграммами, (рис.3.5), построенными в предположении отсутствия ошибок в групповом сигнале Y'_гр = Y_гр .

Определим коэффициент корреляции между групповым сигналом и одним из адресов для рассматриваемой трехканальной системы с мажоритарным уплотнением. Так как функции Уолша, используемые в качестве адресов, ортогональны, то любые пары кодовых комбинаций совпадают на n/2 позициях и отличаются на n/2 позициях. Следовательно, на n/2 позициях, в которых символы па­ры адресов падают, третий канал не влияет на значение груп­пового сигнала. На позициях, в которых символы пары отличаются, значение группового сигнала определяется третьим каналом и одним из пары. Легко убедиться, что таких позиций -n/4 .Таким образом, число позиций, в которых групповой сигнал совпадает с

кодом одного из каналов -n_совп = n/2 + n/4 =3n/4 . Из (3.11) находится коэффициент корреляции

Такой же результат можно получить, используя выражение (3.8), при N= З.Если значность передаваемых кодовых комбинаций n=8,то /r_j0/= 4 ,что позволяет исправлять все однократные ошибки,.

Описание лабораторной установки

Установка состоит из передающей и приемной частей и имеет 3 канала, уплотняемые по мажоритарному принципу. По каждому ка­налу передается сообщения, представленные 4- разрядными дво­ичными числами. Предусмотрен ручной набор трех произвольных 8-разрядных адресов (в тон числе и функций Уолша), произвольных входных кодовых слов и набор любого сочетания ошибки группового сигнала.