
- •Предисловие
- •Теория, примеры и задачи
- •§ 1. Системы двух уравнений
- •1.1. Теория и примеры
- •1.2. Задачи
- •§ 2. Симметрия относительно выражений
- •2.1. Теория и примеры
- •2.2. Задачи
- •§ 3. Cистемы трех уравнений
- •3.1. Теория и примеры
- •3.2. Задачи
- •Ответы
- •§ 1. Системы двух уравнений
- •§ 2. Симметрия относительно выражений
- •§ 3. Системы трех уравнений
- •Биографические справки
- •Список литературы

§ 3. Cистемы трех уравнений
3.1. Теория и примеры
50 70 Докажем теорему Виета для случая многочлена
3-й степени. Пусть многочлен представлен в виде
3 + 2 + + |
(4) |
и имеет вещественные корни 1, 2 и 3. Тогда его можно разложить в произведение линейных членов:
3 + 2 + + = ( − 1)( − 2)( − 3).
Раскроем скобки и приведем подобные:
( − 1)( − 2)( − 3) =
= 3 − ( 1 + 2 + 3) 2 + ( 1 2 + 1 3 + 2 3) − 1 2 3.
Приравняем коэффициенты при степенях :
|
|
1 + 2 + 3 = − , |
|
|
|
|
(5) |
1 2 + 1 3 + 2 3 = , |
|
1 2 3 = − . |
|
|
|

§ 3. Cистемы трех уравнений |
55 |
|
|
Теорема 5 (теорема Виета). Если 1, 2 и 3 – корни многочлена (4), то их сумма равна коэффициенту при 2 с противоположным знаком, сумма попарных произведений – коэффициенту при , а произведение 1 2 3 – свободному члену с противоположным знаком (5).
Теорема 6 (обратная теорема Виета). Если перемен- ные 1, 2 и 3 удовлетворяют условиям (5), то они являются корнями многочлена (4).
Определение 7. Многочлен ( , , ) от трех переменных
, и будем называть симметрическим, если в результате любых перестановок входящих в него переменных , и получается многочлен, тождественный исходному.
Например, ( , , ) ≡ ( , , ). Следует обратить внимание на то, что симметричностью многочлен обладает только относительно заданного набора переменных. Так, многочлен + симметричен относительно и , но несимметричен относительно , и .
Как и в случае двух переменных, симметрическими мо-
гут быть не только многочлены, но и другие выражения,
2 + 2 + 2 √ √ √
например: + + , 2 + 2 + 2 , 2 + 2 + 2 . Определение 8. Выражение ( , , ) от трех перемен-
ных , и будем называть симметрическим, если
в результате любых перестановок входящих в него

56 Теория, примеры и задачи
переменных , и получается выражение, тождествен-
ное исходному.
Определение 9. Многочлены 1 = + + ,
2 = + + и 3 = – элементарные симметрические многочлены от переменных , и .
Приведем без доказательства две теоремы.
Теорема 6. Если в любом многочлене ( 1, 2, 3) вместо
1, 2 и 3 подставить соответственно + + , + +
и , то получится симметрический многочлен.
Теорема 7. Любой симметрический многочлен от , и
можно представить в виде многочлена от 1 = + + ,
2 = + + и 3 = . В частности:
+ + = 1,
2 + 2 + 2 = 12 − 2 2, |
|
3 + 3 + 3 = 13 − 3 1 2 + 3 3, |
|
4 + 4 + 4 = 14 − 4 12 2 + 2 22 + 4 1 3. |
(6) |
§ 3. Cистемы трех уравнений |
57 |
|
|
Еще три полезных тождества:
2 + 2 + 2 + 2 + 2 + 2 = 1 2 − 3 3,
2 2 + 2 2 + 2 2 = 22 − 2 1 3,
3 + 3 + 3 + 3 + 3 + 3 = 12 2 − 2 22 − 1 3.
(7)
Определение 10. Уравнение, в которое входят только симметрические по заданному набору переменных выражения, будем называть симметрическим.
Пример 24.
+ + = −2,
+ + = −5,
= 6.
Решение. Согласно обратной теореме Виета , и долж-
ны быть корнями многочлена 3 + 2 2 −5 −6. Ищем целые
корни среди делителей свободного члена (−6). Подстанов-
ка показывает, что одним из корней будет 1 = −1. В таком случае наш многочлен должен без остатка делиться на + 1.
58 |
|
|
|
|
|
Теория, примеры и задачи |
|
|
|
|
|
|
|
|
|
|
3+2 2−5 −6 |
|
+ 1 |
|
|||
|
|
||||||
|
3 + 2 |
|
|
|
2 + − 6 |
||
|
|
2 |
−5 |
|
|
|
|
|
|
2 |
+ |
|
|
|
|
|
|
|
−6 −6 |
|
|
|
|
|
|
|
−6 −6 |
|
|
|
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
Найдем корни частного 2 + − 6 и запишем:
3 + 2 2 − 5 − 6 = ( + 1)( 2 + − 6) = ( + 1)( + 3)( − 2).
Таким образом, многочлен имеет три корня: 1 = −1,2 = −3 и 3 = 2. В силу симметричности системы уравнений, ее решениями будут все возможные перестановки этих значений: 1 = −1, 1 = −3, 1 = 2; 2 = −1, 2 = 2,2 = −3 и т. д.
Ответ: (−1; −3; 2), (−1; 2; −3), (−3; −1; 2), (−3; 2; −1),
(2; −1; −3), (2; −3; −1).
Пример 25.
+ + = 3,
+ + = 1,
= −2.

§ 3. Cистемы трех уравнений |
59 |
|
|
Решение: , и должны быть корнями многочлена3−3 2+ +2. Ищем целые корни среди делителей свободного члена 2. Подстановка показывает, что одним из корней будет 1 = 2. В таком случае наш многочлен должен без остатка делиться на ( − 2).
3−3 2 |
+ +2 |
− 2 |
3−2 2 |
|
2 − − 1 |
− 2 + − 2+2
− +2
− +2
0
|
|
|
|
1−√ |
|
|
1+√ |
|
|
Найдем корни трехчлена |
2 |
: |
= |
5 |
и 3 = |
5 |
|||
|
2 . |
||||||||
|
|
− − 1 2 |
2 |
|
|||||
( √ )( √ )
3 − 3 2 + + 2 = ( − 2) − 1 − 5 − 1 + 5 . 2 2
В силу симметричности системы уравнений, ее решениями
будут все возможные перестановки значений 1, |
2 |
и 3. |
|
||||||||||||||||||||||||||||||||||||||
|
1+√5 |
|
|
|
√ |
|
|
1 |
√ |
|
|
|
|
|
|
√ |
|
|
|
|
√ |
|
)1 √(5 |
√ |
|
|
|
√ |
|
|
) |
||||||||||
|
(1 √5 |
|
|
√5 )1+√(5 |
|
|
|
|
|
1+√5 |
|
2 |
|
|
2 |
|
|
||||||||||||||||||||||||
Ответ: |
2; |
1−2 |
5 |
; |
|
1+ 5 |
, |
2; |
1+ |
5 |
|
; |
1−2 |
5 |
, |
|
|
1− 5 |
; 2; |
1+ 5 |
, |
||||||||||||||||||||
2 |
|
|
2 |
|
|
|
|
|
|||||||||||||||||||||||||||||||||
( |
|
|
|
−2 |
|
), |
( |
|
|
−2 |
|
; |
|
|
; 2), |
( |
|
|
|
|
; |
−2 |
|
; 2). |
|
|
|
|
|
|
|||||||||||
|
; 2; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
2 |
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|||||||||||||||||||||||||||
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
Теория, примеры и задачи |
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Пример 26. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
|
+ |
= 3, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
+ |
+ |
= 3, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
+ = 3. |
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Решение. Введем |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
обозначения: |
|
|
|
|
|
|
|
|||||||||
= |
|
|
, |
|
|
|
|
|
|
+ + = 3, |
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
= , |
|
|
|
|
+ + = 3, |
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
= |
|
. |
|
|
|
|
= 1. |
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения , |
|
и |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
должны |
быть |
корнями многочлена |
||||||||||||||||
3 − 3 2 + 3 |
− 1 |
( |
− 1)3 = |
0. Три |
совпадающих |
|||||||||||||||||
корня. Следовательно, = = |
|
|
|
|
|
|||||||||||||||||
|
= |
|
= |
|
|
= 1. Далее |
||||||||||||||||
|
|
|
||||||||||||||||||||
= = . Из условия + + = 3 следует = = = 1.
Ответ: (1; 1; 1).
Пример 27.
+ + = 6,
2 + 2 + 2 = 12,
4 + 4 + 4 = 48.
§ 3. Cистемы трех уравнений |
|
|
|
61 |
||||
|
||||||||
Решение. Воспользуемся формулами (6) на с. 56. |
||||||||
|
|
|
2 |
|
|
|
|
|
|
+ + = 1, |
|
1 |
= 6, |
|
|
|
|
+ + = 2, |
1 |
− |
2 2 = 12, |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
− |
2 |
2 |
+ 4 1 3 |
= 48. |
= 3; |
1 |
4 1 2 |
+ 2 2 |
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Применяя поочередную подстановку, находим 1, 2, 3.
1 = 6, |
+ + = 6, |
2 = 12, |
+ + = 12, |
3 = 8. |
= 8. |
Значения , и должны быть корнями многочлена
3 − 6 2 + 12 − 8 ( − 2)3 = 0. Три совпадающих корня. Следовательно, = = = 2.
Ответ: (2; 2; 2).
Пример 28.
+ + = 2,
( + )( + ) + ( + )( + ) + ( + )( + ) = 1,
2( + ) + 2( + ) + 2( + ) = −6.
Решение. Раскроем скобки во втором и третьем уравнениях системы и обратимся к формулам (6) и (7) на с. 56.
62 |
|
|
|
|
Теория, примеры и задачи |
||
|
|
|
|||||
Систему можно переписать в виде |
|
|
|||||
1 = 2, |
2 |
|
2 2 = 1, |
1 = 6, |
1 = 6, |
||
3 2 + 1 |
− |
2 |
= 3, |
2 = 3, |
|||
|
|
|
|
− |
|
− |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 2 − 3 3 |
= −6; |
−6 − 3 3 = −6; |
3 = 0. |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Значения |
, |
и должны быть корнями |
многочлена |
||||
3 − 2 2 − 3 = ( 2 − 2 − 3) 1 = 0, 2 = −1, 3 = 3.
Ответ: (−1; 0; 3), (−1; 3; 0), (0; −1; 3), (0; 3; −1), (3; −1; 0),
(3; 0; −1).
Пример 29.
2 + 2 + 2 = 12,
+ + = 12.
Решение. Вычтем из левой части первого уравнения левую часть второго, соответственно – из правой правую.
2 + 2 + 2 − + + = 0,
+ + = 12.
Умножим левую и правую части первого уравнения на 2.
2 2 + 2 2 + 2 2 − 2 + 2 + 2 = 0
( 2 − 2 + 2) + ( 2 − 2 + 2) + ( 2 − 2 + 2) = 0
( − )2 + ( − )2 + ( − )2 = 0 = = . Подставив

§ 3. Cистемы трех уравнений |
63 |
|
|
в уравнение 2 + 2 + 2 = 12 переменную вместо и , получим: 3 2 − 12 = ±2.
Ответ: (2; 2; 2), (−2; −2; −2).
Пример 30. Решить систему уравнений с параметром :
+ + = 2,
2 + 2 + 2 = ,
3 + 3 + 3 = 8.
Решение. Обратимся к формулам (6) на с. 56.
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|||||||
|
1 |
= 2, |
|
|
|
|
|
|
|
|
|
|
1 = 2, |
|
|
||||||||||
1 |
− |
2 2 = , |
|
|
|
|
2 = −2 , |
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
− 3 1 3 + 3 3 = 8. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
|
|
3 = 4 − . |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4−2 |
|
|
|||
3 − 2 2 + |
− (4 − ) = 0 |
( − 2) |
2 + |
= 0. Все |
|||||||||||||||||||||
корни будут вещественными только |
при |
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
( |
4−2 |
|
≤ 0), т. е. при |
|||||
: |
|
|
|
|
|
2 = − |
|
−4 |
, 3 |
= |
|
−4 |
|
|
|
|
|
|
|
|
|
||||
≥ 4 1 = 2, |
2 |
|
|
2 . |
|
|
|
|
|
|
|
|
|||||||||||||
Ответ: при < 4 |
система не имеет решений, |
|
|
||||||||||||||||||||||
|
√ |
|
|
√ |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
при |
= 4 : (2; 0; 0), (0; 2; 0), (0; 0; 2), |
|
||||||||
|
|
|
(2; −√ |
|
|
; √ |
|
|
), |
(2; √ |
при |
|
> 4 : |
−2 |
4 |
−2 |
4 |
||||
−4 2
√
; −
−4 2
)
,
(−√ |
|
|
; 2; √ |
|
|
), |
( √ |
|
|
; 2; −√ |
|
|
), |
(−√ |
|
|
|
√ |
|
|
; 2), |
||
4−2 |
4−2 |
|
−2 |
|
−2 |
|
−2 |
; |
|
−2 |
|||||||||||||
|
|
4 |
|
|
4 |
|
|
4 |
|
4 |
|
|
4 |
|
|
4 |
|
||||||
( √ |
|
|
; −√ |
|
|
; 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
−2 |
|
−2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
64 |
Теория, примеры и задачи |
|
|
Следующие три примера рассчитаны на «продвинутого» старшеклассника, дружащего с комплексными числами и производными.
Пример 31. Определить, при каких значениях параметров и система имеет ровно одно вещественное решение и найти это решение.
+ + = 3 ,
+ + = 3 ,
= 1.
Решение. Рассмотрим многочлен
( ) = 3 − 3 2 + 3 − 1. |
(8) |
Из теории известно, что многочлен 3-й степени может иметь один или три вещественных корня. Если вещественный корень один (два других комплексные), то система не имеет вещественных решений. Если многочлен имеет три вещественных корня: 1, 2 и 3, то решениями исход- ной системы уравнений будут тройки ( ; ; ), полученные из всех возможных перестановок 1, 2 и 3. В частности, если мы имеем три различных корня, система будет иметь 3! = 6 решений. Одно решение возможно только тогда,
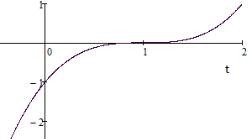
§ 3. Cистемы трех уравнений |
65 |
|
|
когда все три корня совпадают, т. е. многочлен можно представить в виде
( ) = ( − )3 = 3 − 3 2 + 3 2 − 3. |
(9) |
Приравняем коэффициеты в правых частях уравнений
8 и 9: |
−3 = −3 , |
|
= 1, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 = 3 2 |
= 1, |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
− 3 |
= −1. |
|
|
|
|
|
|
|
|
|
|
= 1. |
|
|
|||
|
|
|
= 1 |
= 1 |
|
|
1 = 2 |
= 3 |
= 1 |
Таким образом, |
|
|
|
и |
|
|
. |
||
( ) = 3 − 3 2 + 3 − 1. График функции ( ) представлен на рис. 7.
Рис. 7. График многочлена ( )
Ответ. Только при условии ( = 1)&( = 1) система имеет ровно одно решение: = = = 1.
66 |
Теория, примеры и задачи |
|
|
А что если задать возмущение одного из параметров, т. е. изменить его на небольшую величину? Например, пусть= 1.001. Построим график уравнения с возмущенным
параметром: ( ) = 3 − 3 2 + 3 · 1.001 − 1. Окажется,
что он визуально неотличим от изображенного на рис. 7 и также пересекает ось абсцисс только в одной точке. Может, и в этом случае у системы будет единственное решение? Нет! Многочлен с возмущенным коэффициентом имеет один вещественный и два комплексных корня. При любом малом возмущении параметров и появляются комплексные корни, и потому система не имеет вещественного решения.
Пример 32. Определить, при каких значениях параметра система не имеет вещественных решений; имеет ровно три; ровно шесть вещественных решений.
+ + = −32 ,
+ + = −6,
= .
Решение. Решениями системы уравнений будут все вещественные тройки чисел ( ; ; ), являющиеся корнями мно-
гочлена ( ) = 3+ 32 2−6 − . Определим вспомогательный многочлен ( ) = 3 + 32 2 − 6 . Его график представлен на
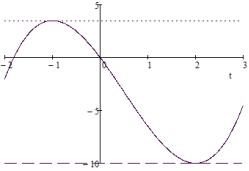
§ 3. Cистемы трех уравнений |
67 |
|
|
рис. 8. Очевидно, ( ) = ( ) − .
Рис. 8. График многочлена ( )
Производная ′( ) = 3 2 − 3 − 6 = 3( − 2)( + 1). Отсюда
(−∞; −1) (2; +∞) – область возрастания функции; (−1; 2)
– область убывания функции; (−1) – точка максимума;
2 – точка минимума. График ( ) получается смещением графика ( ) вверх или вниз в зависимости от знака . На рис. 9а показан график функции ( ) − 3.5, а на рис. 9б – график функции ( ) + 10. Графики соответствуют случаям, когда ( ) имеет три вещественных корня, два из которых кратны (при = 3.5 или = −10). Тогда при
(−10; 3.5) ось пересечет график функции в трех точках – три различных корня, а при (−∞; −10) (3.5; +∞) – только один вещественный корень. Теперь мы можем сформулировать ответ.
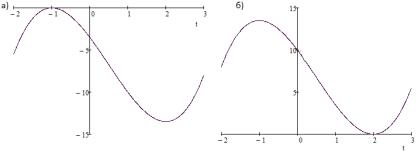
68 |
Теория, примеры и задачи |
|
|
Рис. 9. Графики многочленов: а) ( ) − 3.5; б) ( ) + 10
Ответ: при (−∞; −10) (3.5; +∞) система не имеет
вещественных решений; при = 3.5 и = −10 имеет ров-
но три вещественных решения; при (−10; 3.5) – ровно
шесть.
Пример 33. При каких значениях параметра система имеет ровно одно решение?
+ + = 3 ,
+ + = 6 ,
= 4 .
Решение. Решение будет единственным, если все три корня многочлена 3 −3 2 +6 −4 совпадают. В таком
случае |
многочлен |
можно представить в виде |
( − )3 |
= 3 − 3 2 |
+ 3 2 − 3. Приравняв коэффициен- |
§ 3. Cистемы трех уравнений |
|
|
|
69 |
||||
|
|
|
|
|
||||
ты многочленов, получим: |
|
|
|
|
||||
3 2= 3 , |
|
2= , |
|
= , |
2) = 0, |
|||
3 = 6 , |
|
= 2 , |
|
( |
− |
|||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
= 4 . |
|
3 |
= 4 . |
|
( − 2)( + 2) = 0. |
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Таким образом, возможны два случая: при = 0 существует единственное решение (0; 0; 0) и при = 2 – (2; 2; 2).
Ответ: = 0 и = 2.
Теорему Виета можно обобщить на многочлены любой степени. Так, для корней многочлена четвертой степени
4 + 3 + 2 + + = ( − 1)( − 2)( − 3)( − 4)
имеют место равенства:
1 + 2 + 3 + 4 = − , |
|
1 2 + 1 3 + 1 4 + 2 3 + 2 4 + 3 4 = , |
|
|
|
|
|
|
|
|
|
1 2 3 + 1 2 4 + 1 3 4 + 2 3 4 = , |
|
|
|
1 2 3 4 = . |
− |
Предоставляем читателю возможность самому определить принцип построения таких систем уравнений.
