
- •Техническая электродинамика
- •Приборы и методики измерений в свч-диапазоне
- •Описание измерительной установки
- •Основные свойства и характеристики волн в вс
- •Экспериментальное определение коэффициента отражения от исследуемой нагрузки
- •Измерение малых кбв («метод вилки»)
- •Контрольные вопросы
- •Т-волны в длинных линиях
- •Плоская волна свободного пространства
- •Конфигурация силовых линий полей в длинных линиях
- •Вектор напряженности магнитного поля в т-волне
- •Вектор напряженности электрического поля в линии
- •Т-волны
- •Волны напряжения и тока длинной линии
- •Связь коэффициента отражения с сопротивлением нагрузки
- •Согласованная линия
- •Несогласованная линия
- •Режим стоячей волны
- •Порядок выполнения работы
- •Контрольные вопросы
- •Волны в волноводах
- •Волноводы. Два класса волн. Волновые уравнения
- •Мембранное и дисперсионное уравнения
- •Граничные условия
- •Поля в волноводе
- •Собственные функции и поперечные волновые числа
- •Критические частоты волноводных мод
- •Поля мод на частотах выше и ниже критической
- •Длина волны и фазовая скорость в волноводе
- •Волна основного типа прямоугольного волновода h01
- •Конфигурация силовых линий основного типа поля
- •Перенос мощности по волноводу
- •Режим бегущей волны
- •Режим смешанных волн
- •Элементы волноводного тракта, используемые в работе
- •Порядок выполнения работы
- •Контрольные вопросы
- •Трансформация сопротивлений отрезками длинных линий
- •Входное сопротивление линии
- •Свойства входного сопротивления линии
- •Короткозамкнутая линия
- •Отрезок линии как трансформатор сопротивления
- •Круговая диаграмма сопротивлений
- •Определение нормированной проводимости по нормированному сопротивлению с помощью круговой диаграммы
- •Привязка линии к диаграмме по кбв и минимуму напряжения.
- •Определение сопротивления нагрузки по кбв и местоположению минимума напряжения
- •Включение в линию передачи трансформирующих отрезков с волновым сопротивлением, отличным от волнового сопротивления основного тракта
- •Порядок выполнения работы
- •Контрольные вопросы
- •Волны в коаксиальной линии при произвольной нагрузке
- •Поле т-волны в коаксиальной линии
- •Погонные параметры коаксиальной линии
- •Коэффициент отражения и импеданс
- •Суперпозиция падающей и отраженной волн
- •Круговая диаграмма
- •Порядок выполнения работы
- •Расчет параметров коаксиальной линии
- •Расчет входных характеристик отрезка коаксиальной линии
- •Варианты заданий к работе
- •Контрольные вопросы
- •Одношлейфное согласование волновода с нагрузкой
- •Входная проводимость линии
- •Расчет входных сопротивлений и проводимостей в линиях с последовательными или с параллельными неоднородностями
- •Нормированные сопротивления и проводимости
- •Индуктивные и емкостные диафрагмы в волноводах
- •Проблема согласования нагрузки с линией передачи
- •Порядок выполнения работы
- •Контрольные вопросы
- •Исследование волноводных четырехполюсников с поперечными неоднородностями
- •Волноводные многополюсники и их матрицы рассеяния
- •Экспериментальное определение элементов s-матриц четырехполюсников с поперечной неоднородностью
- •Порядок выполнения работы
- •Контрольные вопросы
- •Согласование линии передачи с нагрузкой в пакете программmicrowaveoffice
- •Теоретические сведения
- •Порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •Содержание
Связь коэффициента отражения с сопротивлением нагрузки
Так
как режимы в линии определяются
сопротивлением нагрузки
![]() ,
включенной на конце линии, то удобно
волны в линии записать через продольную
координату, отсчитываемую от нагрузки
в сторону генератора
,
включенной на конце линии, то удобно
волны в линии записать через продольную
координату, отсчитываемую от нагрузки
в сторону генератора![]() ,
где
,
где![]() – длина линии (см. (1.7)). Тогда из (2.18),
(2.19) легко получить:
– длина линии (см. (1.7)). Тогда из (2.18),
(2.19) легко получить:
![]() (2.0)
(2.0)
 (2.0)
(2.0)
где
![]() – комплексные амплитуды падающих «–»
и отраженных «+» волн на конце линии (на
нагрузке):
– комплексные амплитуды падающих «–»
и отраженных «+» волн на конце линии (на
нагрузке):
 (2.0)
(2.0)
 (2.0)
(2.0)
Где
![]() – модуль и фаза коэффициента отражения
от нагрузки
– модуль и фаза коэффициента отражения
от нагрузки![]() .
Используя закон Ома и соотношения
(2.25), (2.26), можно определить связь
коэффициента отражения и комплексного
сопротивления нагрузки
.
Используя закон Ома и соотношения
(2.25), (2.26), можно определить связь
коэффициента отражения и комплексного
сопротивления нагрузки![]()
 (2.0)
(2.0)
где
![]() – комплексные амплитуды напряжения и
тока на нагрузке. Из формулы (2.27) легко
получить обратную формулу для
– комплексные амплитуды напряжения и
тока на нагрузке. Из формулы (2.27) легко
получить обратную формулу для![]() :
:
 (2.0)
(2.0)
где
 – нормированное сопротивление нагрузки.
– нормированное сопротивление нагрузки.
Согласованная линия
Из формулы (2.28) следует условие согласования:
![]() (2.0)
(2.0)
что
означает
![]() коэффициент отражения от нагрузки
коэффициент отражения от нагрузки![]() при подстановке (2.29) в (2.28) обращается в
нуль:
при подстановке (2.29) в (2.28) обращается в
нуль:
![]() (2.0)
(2.0)
В
этом случае
![]() Отношение напряжения к току на нагрузке
точно соответствует отношению амплитуд
напряжения и тока падающей волны. Вся
мощность, переносимая падающей волной,
поглощается в активном сопротивлении
нагрузки
Отношение напряжения к току на нагрузке
точно соответствует отношению амплитуд
напряжения и тока падающей волны. Вся
мощность, переносимая падающей волной,
поглощается в активном сопротивлении
нагрузки![]() Длинная линия согласована с нагрузкой,
в ней устанавливается режим бегущей
волны. Подстановка (2.30) в (2.23) и (2.24) дает:
Длинная линия согласована с нагрузкой,
в ней устанавливается режим бегущей
волны. Подстановка (2.30) в (2.23) и (2.24) дает:
 (2.0)
(2.0)
Амплитуда
напряжения вдоль линии не меняется:
![]()
Входное
сопротивление линии в любом поперечном
сечении с координатой
![]() ,
равное отношению комплексных амплитуд
напряжения и тока в данном сечений линии
,
равное отношению комплексных амплитуд
напряжения и тока в данном сечений линии неизменно вдоль линии и равно ее волновому
сопротивлению
неизменно вдоль линии и равно ее волновому
сопротивлению![]()
Несогласованная линия
Если
отрезок линии нагружен на конце на
двухполюсник с сопротивлением
![]() то, в отличие от (2.31), наряду с падающей
волной в линии возникает отраженная
волна, бегущая от нагрузки к генератору.
Распределение напряжения и тока в линии
равно в этом случае сумме прямой и
обратной волн (2.18), (2.19) напряжений и
токов соответственно. Из этих формул
легко получить распределения вдоль
линии модулей напряжения
то, в отличие от (2.31), наряду с падающей
волной в линии возникает отраженная
волна, бегущая от нагрузки к генератору.
Распределение напряжения и тока в линии
равно в этом случае сумме прямой и
обратной волн (2.18), (2.19) напряжений и
токов соответственно. Из этих формул
легко получить распределения вдоль
линии модулей напряжения![]() и тока
и тока![]() нормированных к модулю амплитуд падающих
волн
нормированных к модулю амплитуд падающих
волн![]()
 (2.0)
(2.0)
 (2.0)
(2.0)
Такой
режим в линии называется режимом
смешанных волн. В линии устанавливается
интерференционная картина распределения
модулей напряжения и тока (рис. 2.3). В тех
сечениях
![]() где прямая и обратная
где прямая и обратная
волны
складываются в противофазе
![]() наблюдается минимум напряжения
наблюдается минимум напряжения![]() и
максимум тока
и
максимум тока![]() из (2.32), (2.33) легко получить:
из (2.32), (2.33) легко получить:
 (2.0)
(2.0)
В
точках
![]() фазы
фазы![]() и
и![]() совпадают и равны нулю. В тех сечениях
совпадают и равны нулю. В тех сечениях![]() где прямая и обратная волны складываются
в фазе
где прямая и обратная волны складываются
в фазе![]() наблюдаются максимумы напряжения
наблюдаются максимумы напряжения![]() и минимумы тока
и минимумы тока![]() из (2.32), (2.33) легко получить:
из (2.32), (2.33) легко получить:
 (2.0)
(2.0)
В
точках
![]() фазы
фазы![]() и
и![]() совпадают
и равны нулю. Отношение модулей
минимального и максимального напряжений
(токов) (2.34), (2.35) называется коэффициентом
бегущей волны (КБВ), а обратная величина
– коэффициентом стоячей волны (КСВ):
совпадают
и равны нулю. Отношение модулей
минимального и максимального напряжений
(токов) (2.34), (2.35) называется коэффициентом
бегущей волны (КБВ), а обратная величина
– коэффициентом стоячей волны (КСВ):
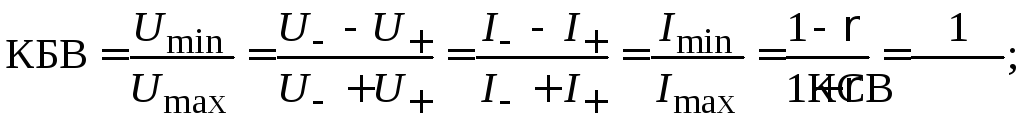 (2.0)
(2.0)
![]() (2.0)
(2.0)
Ф ормулы
(2.36) и (2.37) являются расчетными. Из формул
(2.23), (2.24) легко получить нормированные
значения функций напряжения
ормулы
(2.36) и (2.37) являются расчетными. Из формул
(2.23), (2.24) легко получить нормированные
значения функций напряжения![]() и
тока
и
тока![]()
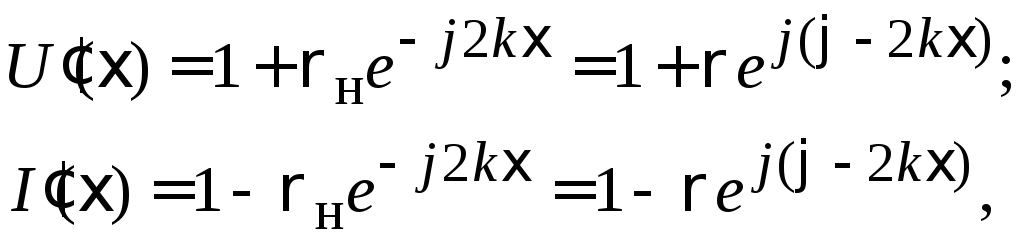 (2.0)
(2.0)
которые
удобно представить в виде векторов на
комплексной плоскости с вещественной
![]() и мнимой
и мнимой![]() осями (рис. 2.3). Модуль коэффициента
отражения не зависит от
осями (рис. 2.3). Модуль коэффициента
отражения не зависит от![]() ,
поэтому с ростом
,
поэтому с ростом![]() конец вектора
конец вектора![]() описывает по часовой стрелке окружность
радиуса
описывает по часовой стрелке окружность
радиуса![]() .
Легко показать, что длина всей окружности
соответствует
.
Легко показать, что длина всей окружности
соответствует![]() .
В процессе поворота
.
В процессе поворота![]() и
и![]() меняются модули
меняются модули![]() и
и![]() от
от![]() до
до![]() .
Значения модулей
.
Значения модулей![]() и
и![]() представлены в виде интерференционного
распределения напряжения и тока вдоль
оси линии
представлены в виде интерференционного
распределения напряжения и тока вдоль
оси линии![]() .
На рис. 2.3, согласно формулам (2.38),
изображены три состояния векторной
диаграммы:
.
На рис. 2.3, согласно формулам (2.38),
изображены три состояния векторной
диаграммы:
при
 (на
нагрузке)
(на
нагрузке)

при
 (в
точке минимума)
(в
точке минимума)

при
 (в
точке максимума)
(в
точке максимума)

Коэффициент
отражения по мощности – это отношение
мощности, переносимой отраженной волной
![]() ,
к мощности, переносимой падающей волной
,
к мощности, переносимой падающей волной![]()
 (2.0)
(2.0)
С
учетом формул (2.39) и (2.31) мощность,
поглощаемая в активном сопротивлении
нагрузки
![]() определится
как
определится
как
 (2.0)
(2.0)
где
![]() – нормированные активное
– нормированные активное![]() и реактивное
и реактивное![]() сопротивления нагрузки. Из (2.40) видно,
что при
сопротивления нагрузки. Из (2.40) видно,
что при![]() и
и![]() (согласованная линия) вся мощность
падающей волны
(согласованная линия) вся мощность
падающей волны![]() поглощается в нагрузке:
поглощается в нагрузке:![]() .
.
