4. Трансформация сопротивлений отрезками длинных линий

Цель работы:изучение свойств длинной линии как трансформатора сопротивлений; расчет и измерение сопротивлений длинной линии с помощью круговой диаграммы.

1. Входное сопротивление линии

Рассмотрим линию длиной , питаемую генератором и нагруженную на сопротивление(рис. 4.1).

В 2 было показано, что напряжение и ток в такой длинной линии могут быть представлены суммой прямой и обратной волн следующим образом:

(4.0)

(4.0)

где – координата вдоль линии, отсчитываемая от нагрузки (от конца линии) в сторону генератора (см. рис. 4.1);– комплексная амплитуда падающей волны напряжения на конце линии (на нагрузке);– комплексная амплитуда падающей волны тока на конце линии (на нагрузке);– волновое сопротивление линии;

(4.0)

Здесь– коэффициент отражения от нагрузки;– модуль коэффициента отражения;– фаза коэффициента отражения;комплексные амплитуды отраженных волн напряжения и тока на конце линии (на нагрузке);– нормированное сопротивление нагрузки. Под входным сопротивлением линии длинойпонимается отношение комплексных амплитуд напряженияи токав сечении линии с координатой; из (4.1) и (4.2), согласно этому определению, легко найти входное сопротивление линии длиной:

(4.0)

где

(4.0)

Подстановка (4.3) в (4.4) позволяет входное сопротивление представить в виде

(4.0)

Из (4.4)–(4.6) видно, что определяется длиной линии, волновым числомk, сопротивлением нагрузкии волновым сопротивлением линии. Формулу (4.6) можно переписать для нормированных значений сопротивлений:

(4.0)

где и– безразмерные комплексные величины:

Из формулы (4.7) может быть получена и формула для входной нормированной проводимости линии:

(4.7.а)

где – нормированная проводимость нагрузки.

Линия длиной с сопротивлением, включенным на ее конце, можно интерпретировать как двухполюсник, а сопротивление(4.7) (или проводимость(4.7.а)) как его входное сопротивление (или входную проводимость). Так как в общем случае распределение напряжения и тока вдоль линии меняется вследствие интерференции падающей и отраженной волн (см. 2), то их отношение, т. е. сопротивление, тоже будет меняться вдоль линии.

2. Свойства входного сопротивления линии

В 2 было показано, что напряжение , токименяются вдоль линии периодически с периодом. Из формулы (4.4) следует, что и сопротивлениеимеет тот же период изменения. Поэтому поведениедостаточно рассмотреть на полуволновом отрезке, заключенном, например, между соседними максимумами напряжения (рис. 4.2). В сечениях линии с координатамиифаза коэффициента отраженияпринимает значение, кратноегде– целое число; коэффициент отраженияположителен,. Поэтому числитель дроби формулы (4.4) принимает максимальное значение, а знаменатель – минимальное значение. Напряжение и ток в линии синфазны. Таким образом, в сечениях линии с координатами,сопротивление линии имеет чисто вещественное и максимальное значение, численно совпадающее с КСВ в линии:

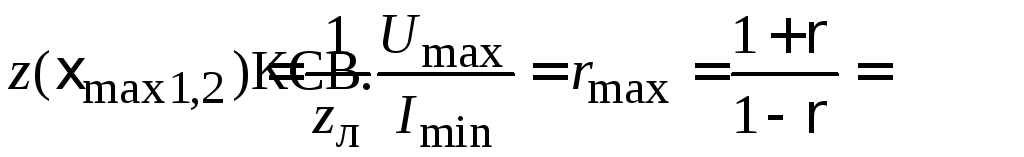(4.0)

На рис. 4.2, а,дприведены векторные диаграммы на комплексной плоскости для этих случаев ().

Как следует из формулы для (4.5), фаза коэффициента отраженияменяется по линейному закону от, так что векторна комплексной плоскости поворачивается по часовой стрелке, а модуль егоостается неизменным. Поэтому в сечении(где) положениебудет, как на рис. 4.2,г. Из этого рисунка видно, что модуль числителя (модуль напряжения)а модуль знаменателяПоэтому сопротивление по модулю будет меньше, чем в сечении:. Поскольку числитель (напряжения) отстает по фазе от знаменателя (тока), то входное сопротивление будет иметь емкостной характер:.

В сечении линии с координатой фаза коэффициента отраженияпринимает, значения, кратные нечетному числугдеm– целое число; коэффициент отраженияотрицателен и равен. Числитель и знаменатель дроби (4.4) снова вещественны (напряжение и ток линии синфазны), сопротивление, как и в сечениях, вещественно и принимает минимальное значение, совпадающее численно с КБВ в линии (рис. 4.2,в):

(4.0)

Нетрудно установить, что в сечении, где модуль сопротивления снова возрастает, а реактивная часть сопротивления имеет индуктивный характер(рис. 4.2,б).