
- •Техническая электродинамика
- •Приборы и методики измерений в свч-диапазоне
- •Описание измерительной установки
- •Основные свойства и характеристики волн в вс
- •Экспериментальное определение коэффициента отражения от исследуемой нагрузки
- •Измерение малых кбв («метод вилки»)
- •Контрольные вопросы
- •Т-волны в длинных линиях
- •Плоская волна свободного пространства
- •Конфигурация силовых линий полей в длинных линиях
- •Вектор напряженности магнитного поля в т-волне
- •Вектор напряженности электрического поля в линии
- •Т-волны
- •Волны напряжения и тока длинной линии
- •Связь коэффициента отражения с сопротивлением нагрузки
- •Согласованная линия
- •Несогласованная линия
- •Режим стоячей волны
- •Порядок выполнения работы
- •Контрольные вопросы
- •Волны в волноводах
- •Волноводы. Два класса волн. Волновые уравнения
- •Мембранное и дисперсионное уравнения
- •Граничные условия
- •Поля в волноводе
- •Собственные функции и поперечные волновые числа
- •Критические частоты волноводных мод
- •Поля мод на частотах выше и ниже критической
- •Длина волны и фазовая скорость в волноводе
- •Волна основного типа прямоугольного волновода h01
- •Конфигурация силовых линий основного типа поля
- •Перенос мощности по волноводу
- •Режим бегущей волны
- •Режим смешанных волн
- •Элементы волноводного тракта, используемые в работе
- •Порядок выполнения работы
- •Контрольные вопросы
- •Трансформация сопротивлений отрезками длинных линий
- •Входное сопротивление линии
- •Свойства входного сопротивления линии
- •Короткозамкнутая линия
- •Отрезок линии как трансформатор сопротивления
- •Круговая диаграмма сопротивлений
- •Определение нормированной проводимости по нормированному сопротивлению с помощью круговой диаграммы
- •Привязка линии к диаграмме по кбв и минимуму напряжения.
- •Определение сопротивления нагрузки по кбв и местоположению минимума напряжения
- •Включение в линию передачи трансформирующих отрезков с волновым сопротивлением, отличным от волнового сопротивления основного тракта
- •Порядок выполнения работы
- •Контрольные вопросы
- •Волны в коаксиальной линии при произвольной нагрузке
- •Поле т-волны в коаксиальной линии
- •Погонные параметры коаксиальной линии
- •Коэффициент отражения и импеданс
- •Суперпозиция падающей и отраженной волн
- •Круговая диаграмма
- •Порядок выполнения работы
- •Расчет параметров коаксиальной линии
- •Расчет входных характеристик отрезка коаксиальной линии
- •Варианты заданий к работе
- •Контрольные вопросы
- •Одношлейфное согласование волновода с нагрузкой
- •Входная проводимость линии
- •Расчет входных сопротивлений и проводимостей в линиях с последовательными или с параллельными неоднородностями
- •Нормированные сопротивления и проводимости
- •Индуктивные и емкостные диафрагмы в волноводах
- •Проблема согласования нагрузки с линией передачи
- •Порядок выполнения работы
- •Контрольные вопросы
- •Исследование волноводных четырехполюсников с поперечными неоднородностями
- •Волноводные многополюсники и их матрицы рассеяния
- •Экспериментальное определение элементов s-матриц четырехполюсников с поперечной неоднородностью
- •Порядок выполнения работы
- •Контрольные вопросы
- •Согласование линии передачи с нагрузкой в пакете программmicrowaveoffice
- •Теоретические сведения
- •Порядок выполнения работы
- •Содержание отчета
- •Контрольные вопросы
- •Содержание
Критические частоты волноводных мод
Согласно
дисперсионным уравнениям (3.6) или (3.7),
продольное волновое число жестко связано
с поперечным волновым числом
![]() и волновым числом среды, заполняющей
волновод
и волновым числом среды, заполняющей
волновод![]() Из (3.7) следует, что в зависимости от
того, какое из чисел окажется больше (
Из (3.7) следует, что в зависимости от
того, какое из чисел окажется больше (![]() или
или![]() ),
продольное волновое число может быть
либо вещественным, либо мнимым. Это
наглядно видно из рис. 3.2, где на числовой
оси отложено конкретное число
),
продольное волновое число может быть
либо вещественным, либо мнимым. Это
наглядно видно из рис. 3.2, где на числовой
оси отложено конкретное число![]() .
В данном случае для первых двух мод
.
В данном случае для первых двух мод![]() – вещественное число, а для всех других
– мнимое. Если зафиксировать форму и
размеры поперечного сечения волновода
(а, следовательно, и все
– вещественное число, а для всех других
– мнимое. Если зафиксировать форму и
размеры поперечного сечения волновода
(а, следовательно, и все![]() ),
а также
),
а также![]() ,
и изменять частоту, то из (3.7) нетрудно
видеть, что для каждой моды существует
частота, ниже которой продольное волновое
число
,
и изменять частоту, то из (3.7) нетрудно
видеть, что для каждой моды существует
частота, ниже которой продольное волновое
число![]() становится
мнимым. Эта частота называется критической
частотой данной моды. Ее легко найти из
(3.7), приравнивая
становится
мнимым. Эта частота называется критической
частотой данной моды. Ее легко найти из
(3.7), приравнивая![]() нулю:
нулю:
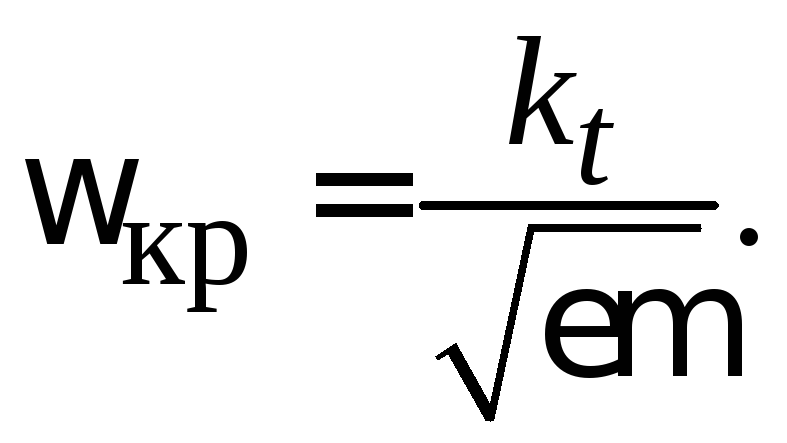 (3.0)
(3.0)
Таким
образом, критическая частота тем выше,
чем выше порядок моды и чем меньше
поперечные размеры волновода и меньше
![]() и
и![]() .
Волна основного типа имеет наименьшую
критическую частоту. Наряду с понятием
критической частоты используется
понятие, критической длины волны:
.
Волна основного типа имеет наименьшую
критическую частоту. Наряду с понятием
критической частоты используется
понятие, критической длины волны:
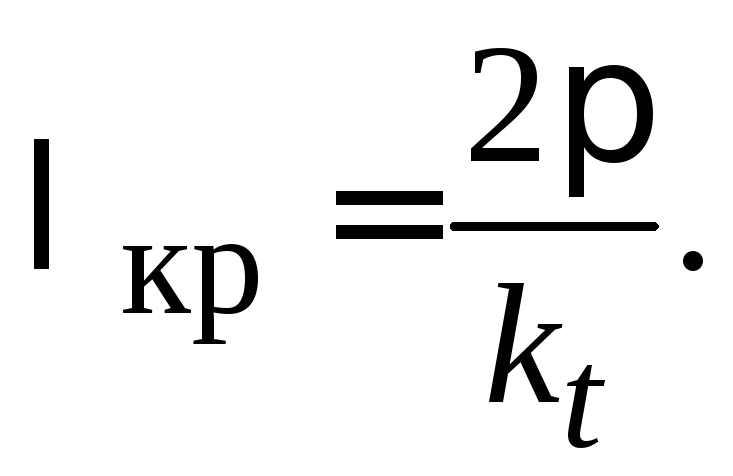 (3.0)
(3.0)
Поля мод на частотах выше и ниже критической
Поведение
одной и той же моды на частотах выше и
ниже критической, совершенно различно.
При
![]() продольное волновое число
продольное волновое число![]() вещественно, и мнимый экспоненциальный
множитель
вещественно, и мнимый экспоненциальный
множитель![]() входящий в выражения (3.10), свидетельствует
о распространении волны вдоль волновода.
Модуль экспоненты не зависит отz(он равен единице), а ее фаза меняется в
зависимости отzпо линейному закону:
входящий в выражения (3.10), свидетельствует
о распространении волны вдоль волновода.
Модуль экспоненты не зависит отz(он равен единице), а ее фаза меняется в
зависимости отzпо линейному закону:![]() Таким образом, в этом случае поля (3.10)
представляют собой незатухающие волны,
бегущие по волноводу в направлениях +zили –z(распространяющиеся волны). Если же
Таким образом, в этом случае поля (3.10)
представляют собой незатухающие волны,
бегущие по волноводу в направлениях +zили –z(распространяющиеся волны). Если же![]() то продольное волновое число
то продольное волновое число![]() – мнимая величина и экспонента в формулах
(3.10) – является вещественной функцией
– мнимая величина и экспонента в формулах
(3.10) – является вещественной функцией![]() где
где![]() .
Фаза полей вдоль волновода не меняется,
а амплитуды либо экспоненциально
убывают, либо экспоненциально возрастают
в зависимости отz(рис. 3.3). Экспоненциальное убывание
(возрастание) будет тем круче, чем больше
.
Фаза полей вдоль волновода не меняется,
а амплитуды либо экспоненциально
убывают, либо экспоненциально возрастают
в зависимости отz(рис. 3.3). Экспоненциальное убывание
(возрастание) будет тем круче, чем больше![]() .
Такие «волны» называются не
распространяющимися волнами, они не
переносят мощность вдоль волновода.
.
Такие «волны» называются не
распространяющимися волнами, они не
переносят мощность вдоль волновода.
Р аспространяющиеся
волны переносят мощность по волноводу,
ибо их поперечные компоненты поля
аспространяющиеся
волны переносят мощность по волноводу,
ибо их поперечные компоненты поля![]() и
и![]() являются синфазными.
являются синфазными.
Длина волны и фазовая скорость в волноводе
Для
распространяющихся волн вводится
понятие длины волны в волноводе
![]() и фазовой скорости
и фазовой скорости![]() с учетом (3.12) формулы для них имеют вид:
с учетом (3.12) формулы для них имеют вид:
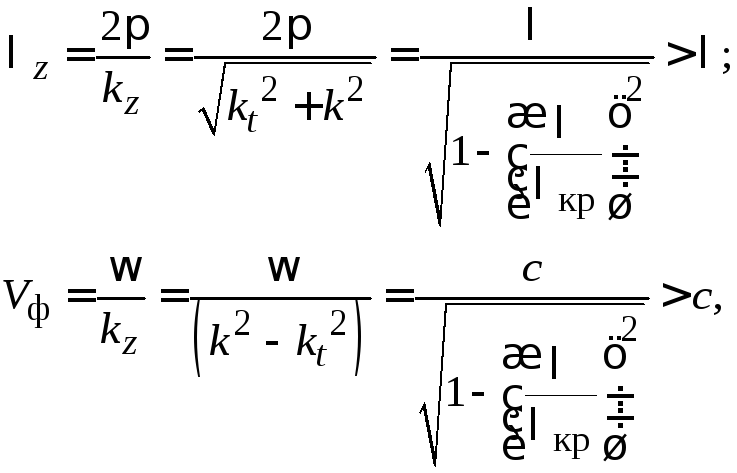 (3.0)
(3.0)
где
![]() – длина волны в среде с проницаемостями
– длина волны в среде с проницаемостями![]() и
и![]() ,
заполняющей волновод;
,
заполняющей волновод;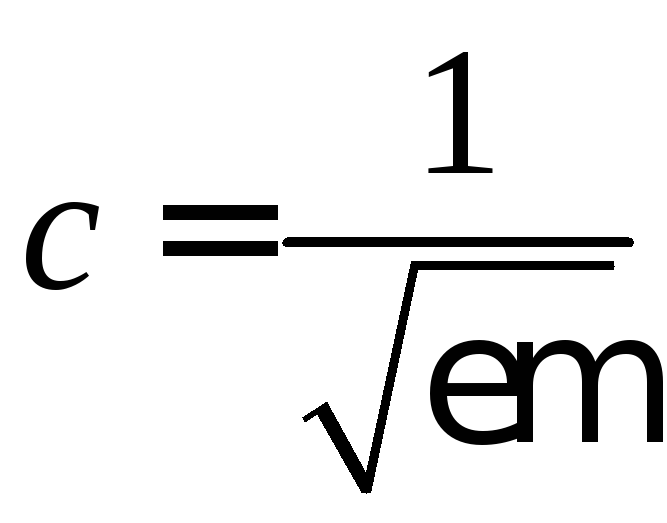 – скорость света в среде, заполняющей
волновод.
– скорость света в среде, заполняющей
волновод.
Из
формул (3.13) следует, что в волноводе
длина волны
![]() всегда больше длины волны в свободном
пространстве
всегда больше длины волны в свободном
пространстве![]() а фазовая скорость
а фазовая скорость![]() больше скорости света в свободном
пространстве
больше скорости света в свободном
пространстве![]() (рис. 3.4).
(рис. 3.4).
Волна основного типа прямоугольного волновода h01
Р ешение
мембранного уравнения (3.5) в прямоугольном
волноводе дляН-волн (3.9) позволяет
найти:
ешение
мембранного уравнения (3.5) в прямоугольном
волноводе дляН-волн (3.9) позволяет
найти:
1) мембранную функцию с точностью до амплитудного множителя С:
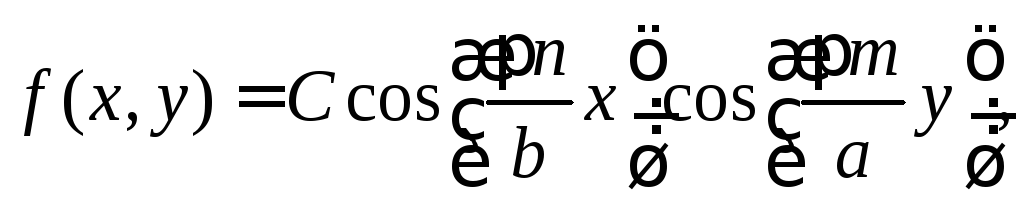 (3.0)
(3.0)
где
![]() – поперечные размеры волновода
(рис. 3.1);
– поперечные размеры волновода
(рис. 3.1);![]()
![]() – декартовые координаты поперечного
сечения прямоугольного волновода;
– декартовые координаты поперечного
сечения прямоугольного волновода;
2) поперечные волновые числа
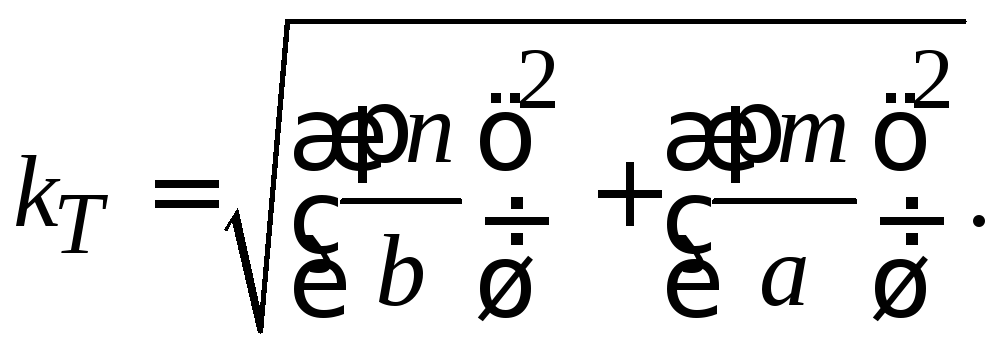 (3.0)
(3.0)
Так
как
![]() ,
то наименьшее поперечное волновое число
получается при
,
то наименьшее поперечное волновое число
получается при![]() тогда для основного типа поля из (3.7),
(3.11)–(3.15) легко найти:
тогда для основного типа поля из (3.7),
(3.11)–(3.15) легко найти:
поперечное
волновое число ![]() (3.0)
(3.0)
критическую
длину волны ![]() (3.0)
(3.0)
критическую
частоту 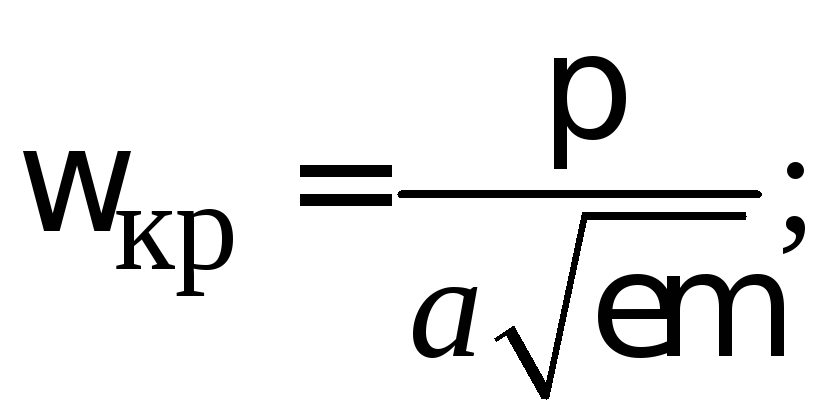 (3.0)
(3.0)
длину
волны в волноводе 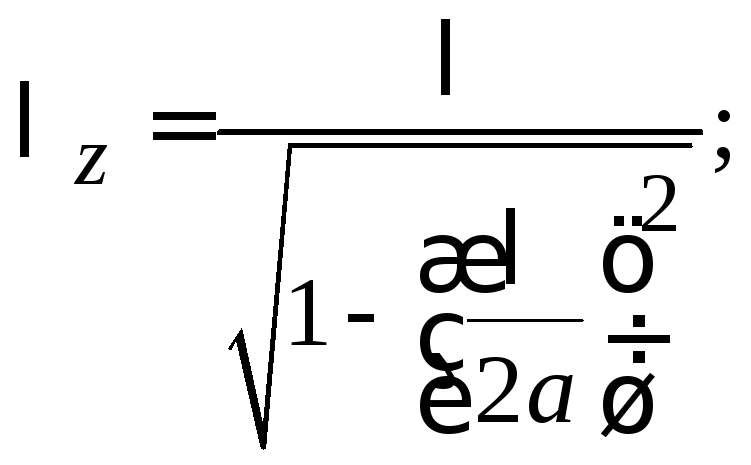 (3.0)
(3.0)
фазовую
скорость в волноводе 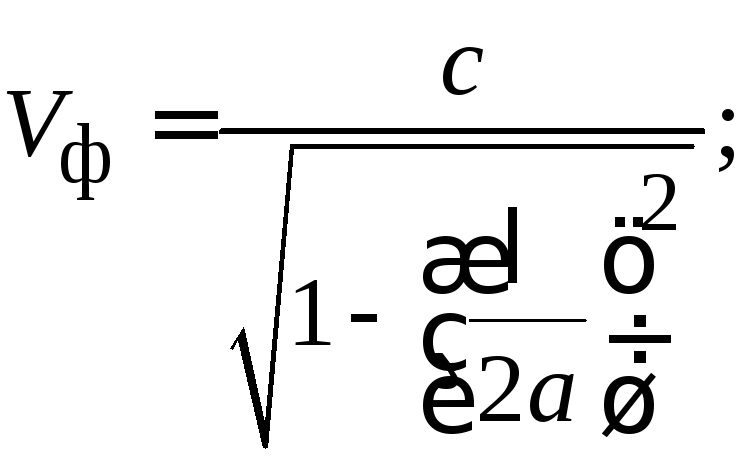 (3.0)
(3.0)
продольное
волновое число 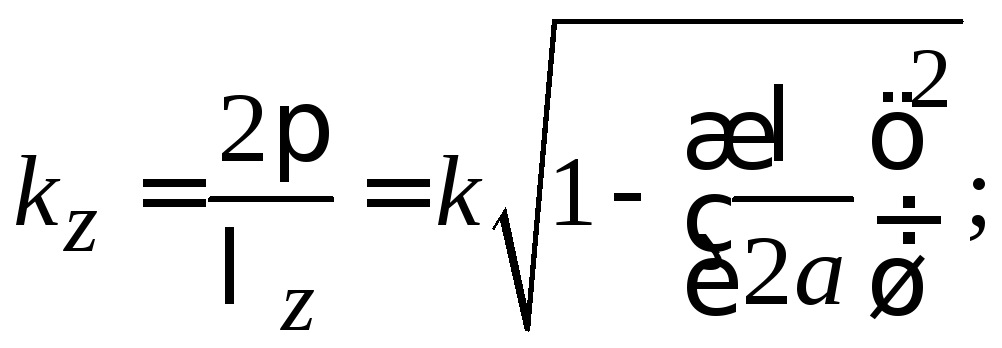 (3.0)
(3.0)
мембранную
функцию 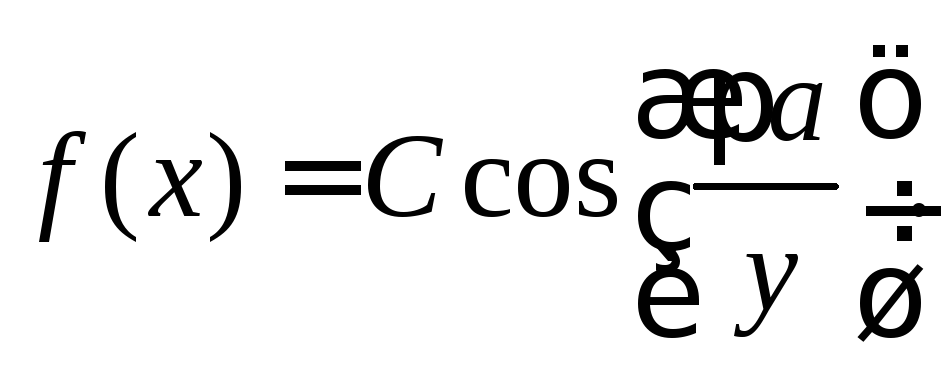 (3.0)
(3.0)
Подстановка
(3.16)–(3.22) в уравнения (3.10) для полей
позволяет определить векторы напряженностей
электрического и магнитного поля волны
основного типа
![]() в прямоугольном волноводе:
в прямоугольном волноводе:
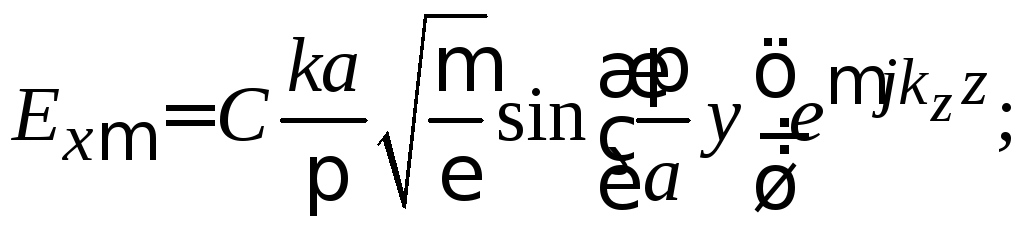 (3.0)
(3.0)
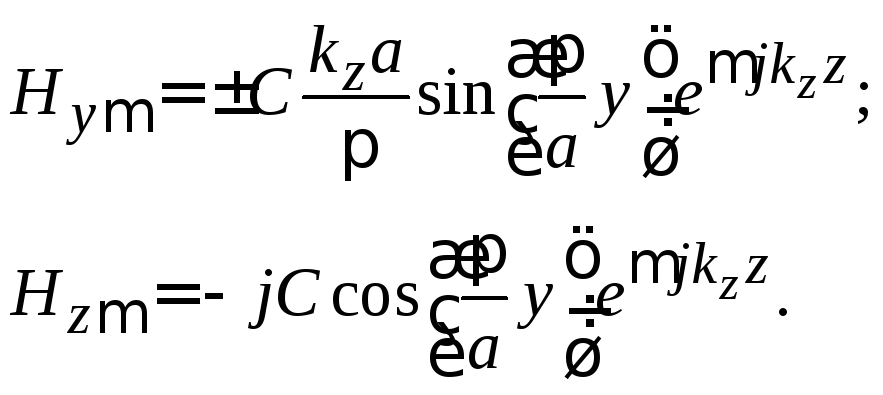 (3.0)
(3.0)
Обычно для сравнения собственных функций волновода между собой производится их нормировка. Нормированные собственные функции удобнее использовать в электродинамических расчетах устройств СВЧ. Вводится понятие нормы N:
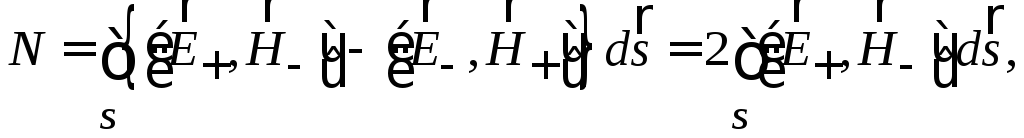 (3.0)
(3.0)
где
S– поперечное сечение волновода;![]()
Подстановка (3.23), (3.24) в (3.25) позволяет взять интеграл и через норму определить амплитудный коэффициент С:
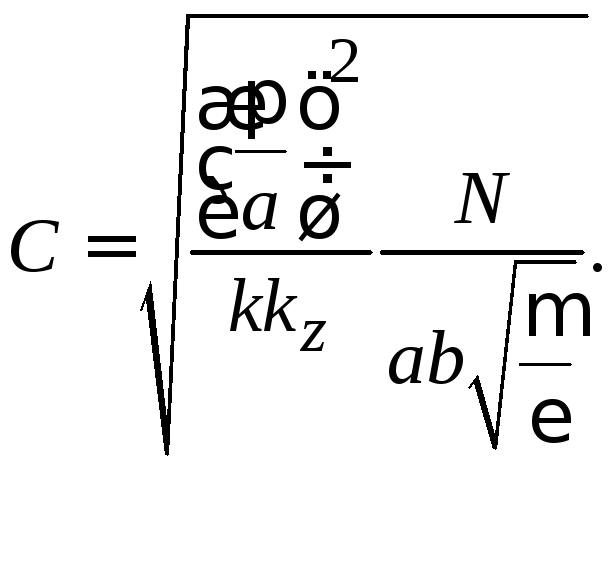 (3.0)
(3.0)
Подстановка
(3.26) в (3.23), (3.24) определяет нормированную
собственную функцию основного типа
прямоугольного волновода
![]() :
:
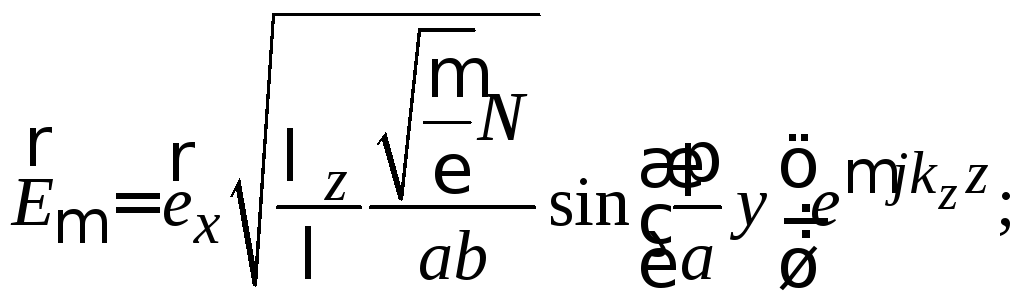 (3.0)
(3.0)
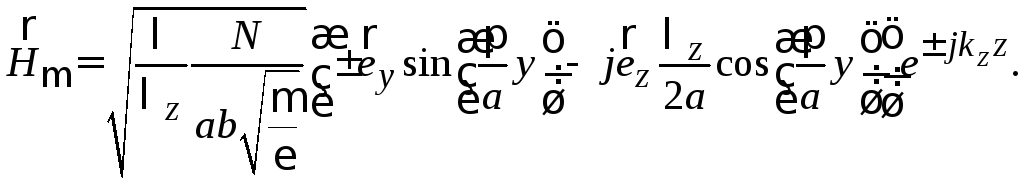 (3.0)
(3.0)
Введение нормированных собственных функций открывает возможность сокращенного описания волнового режима в волноводе: вместо подробной записи полей всех имеющихся мод как функции координат достаточно указать только их амплитуды. Выбор величины нормы Nпроизволен, и чаще всего величина не выбирается, а просто фиксируется как константа, имеющая размерность мощности. При определении мощности, переносимой полем волновода, как правило, выбирают величинуN = 1Вт.
