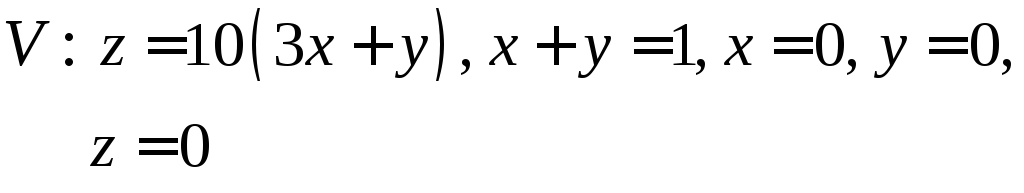Вычисление криволинейного интеграла
Теорема.
Пусть L
- кривая,
заданная уравнениями
,
,
,
где
и
непрерывны на
вместе со своими производными, а
функции
и
непрерывны вдоль кривойL.
Тогда существует криволинейный
интеграл J
и справедливо равенство
=
.
Следствие.
Если кривая
L
задана уравнением
,
,
причем функция
имеет кусочно-непрерывную производную,
а функции
и
- кусочно- непрерывны вдоль кривойL,
то существует криволинейный
интеграл J
и справедливо равенство
=
.
Пример 24.
Вычислим криволинейный интеграл I=
,
где криваяL
задана уравнением
и соединяет точкиA
(1, 1) и
B
(-1, 1).
Учитывая, что
,
,
иx
изменяется от 1 до -1, по формуле для
вычисления криволинейного интеграла
(см. следствие из
теоремы) имеем
I
=
.
Пример 25.
Вычислим интеграл I
=
,
гдеL
- окружность
.
Выпишем параметрические
уравнения данной окружности:
,
,
.
Вычислим интеграл, используя теорему
и учитывая, что
,
.
I
=
=
.
Формула Грина. Условия независимости криволинейного интеграла от пути интегрирования.
Теорема.
Если функции
,
и их частные производные
,
непрерывны в ограниченной областиD
с кусочно-гладкой
границей L,
то справедливо равенство
=
.
Это равенство называется формулой Грина.
Напомним, что область D называется односвязной, если для любого замкнутого контура, лежащего в этой области, ограниченная им часть плоскости целиком принадлежит области D.
Теорема.
Пусть функции
,
и их частные производные
,
непрерывны в односвязной областиD.
Тогда следующие условия эквивалентны:
Для любого замкнутого кусочно-гладкого контура L, расположенного в области D, справедливо равенство
=0.
Для любых двух точек A и B в области D криволинейный
интеграл
не зависит от формы пути интегрирования,
расположенного в областиD.
3. Выражение
является полным дифференциалом, т.е. в
областиD
существует функция
,
такая, что
.
При этом для
любой кусочно-гладкой кривой AB,
лежащей в области D,
имеет место равенство
=
.
В области D выполняется равенство
=
.
Замечание.
Функция
из условия 3 может быть найдена по формуле
=
,
где интеграл в правой части берется по
произвольной кривойAB,
лежащей в области D
и соединяющей
какую-нибудь фиксированную точку
с точкой
(c
- произвольная постоянная). В качестве
кривой AB
удобно бывает брать ломаную, состоящую
из двух отрезков, параллельных осям
координат.
Пример 25.
Найдем функцию
,
если
.
Сначала убедимся,
что функция
действительно существует, т.е. выполнено
равенство
=
.
В нашем примере
,
,
.
Функцию
будем искать по формуле
=
;
интеграл в правой части вычислим по
кривойL,
соединяющей точку
с точкой
и представляющей собой ломаную, состоящую
из двух отрезков, параллельных осям
координат:
.
На отрезке
,
следовательно,
;
на отрезке
,
поэтому
.
=
=
.
Контрольная работа № 9
|
Вариант 1 |
Вариант 2
|
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8.
|
|
9.
|
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
|
Вариант 3 |
Вариант 4
|
|
1. Измените порядок интегрирования в повторном интеграле
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8. |
|
9.
|
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
-
отрезок
,
-
отрезок
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
|
Вариант 5 |
Вариант 6
|
|
1. Измените порядок интегрирования в повторном интеграле
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8.
|
|
9.
|
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
|
Вариант 7 |
Вариант 8
|
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8.
|
|
9.
|
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
-
отрезок
,
|
Вариант 9 |
Вариант 10
| |
| ||
|
|
| |
|
В заданиях 2- 5 вычислите интегралы
| ||
|
2.
|
2.
| |
|
3.
|
3.
| |
|
4.
|
4.
| |
|
5.
|
5.
| |
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| ||
|
6.
|
6.
| |
|
7.
|
7.
| |
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| ||
|
8.
|
8.
| |
|
9.
|
9.
| |
|
В задании 10 вычислите криволинейный интеграл.
| ||
|
10.
|
10.
| |
|
Вариант 11 |
Вариант 12
| |
| ||
|
|
| |
|
В заданиях 2- 5 вычислите интегралы
| ||
|
2.
|
2.
| |
|
3.
|
3.
| |
|
4.
|
4.
| |
|
5.
|
5.
| |
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| ||
|
6.
|
6.
| |
|
7.
|
7.
| |
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| ||
|
8.
|
8.
| |
|
9. |
9.
| |
|
В задании 10 вычислите криволинейный интеграл.
| ||
|
10.
|
10.
| |
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
|
Вариант 13 |
Вариант 14
|
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8.
|
|
9 |
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
|
Вариант 15 |
Вариант 16
|
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2.
|
2.
|
|
3.
|
3.
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8.
|
|
9.
|
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
|
Вариант 17 |
Вариант 18
|
|
1. Измените порядок интегрирования в повторном интеграле
| |
|
|
|
|
В заданиях 2- 5 вычислите интегралы
| |
|
2.
|
2.
|
|
3.
|
3
|
|
4.
|
4.
|
|
5.
|
5.
|
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| |
|
6.
|
6.
|
|
7.
|
7.
|
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| |
|
8.
|
8.
|
|
9. |
9.
|
|
В задании 10 вычислите криволинейный интеграл.
| |
|
10.
|
10.
|
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, 
, 
,
,
,
,
,
,
,
,
,
-
отрезок
,
-
отрезок
|
Вариант 19 |
Вариант 20
|
| ||
|
| |||
|
|
|
| ||
|
В заданиях 2- 5 вычислите интегралы
|
| |||
|
2.
|
2.
|
| ||
|
3.
|
3.
|
| ||
|
4.
|
4.
|
| ||
|
5.
|
5.
|
| ||
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
|
| |||
|
6.
|
6.
|
| ||
|
7.
|
7.
|
| ||
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
|
| |||
|
8.
|
8.
|
| ||
|
9.
|
9.
|
| ||
|
В задании 10 вычислите криволинейный интеграл.
|
| |||
|
10.
|
10.
|
| ||
|
Вариант 21 |
Вариант 22
| |||
|
1. Измените порядок интегрирования в повторном интеграле
| ||||
|
|
| |||
|
В заданиях 2- 5 вычислите интегралы
| ||||
|
2.
|
2.
| |||
|
3.
|
3.
| |||
|
4.
|
4.
| |||
|
5.
|
5.
| |||
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| ||||
|
6.
|
6.
| |||
|
7.
. |
7.
| |||
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| ||||
|
8.
|
8.
| |||
|
9.
|
9.
| |||
|
В задании 10 вычислите криволинейный интеграл.
| ||||
|
10.
|
10.
| |||
|
Вариант 23 |
Вариант 24
|
| ||
|
| |||
|
|
|
| ||
|
В заданиях 2- 5 вычислите интегралы
|
| |||
|
2.
|
2.
|
| ||
|
3.
|
3.
|
| ||
|
4.
|
4.
|
| ||
|
5.
|
5.
|
| ||
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
|
| |||
|
6.
|
6.
|
| ||
|
7.
|
7.
|
| ||
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
|
| |||
|
8.
|
8.
|
| ||
|
9.
|
9.
|
| ||
|
В задании 10 вычислите криволинейный интеграл.
|
| |||
|
10.
|
10.
|
| ||
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
, 
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
-
отрезок
,
|
Вариант 25 |
Вариант 26
| |
|
1. Измените порядок интегрирования в повторном интеграле
| ||
|
|
| |
|
В заданиях 2- 5 вычислите интегралы
| ||
|
2.
|
2.
| |
|
3.
|
3
| |
|
4.
|
4.
| |
|
5.
|
5.
| |
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| ||
|
6.
|
6.
| |
|
7.
|
7.
. | |
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| ||
|
8.
|
8.
| |
|
9.
|
9.
| |
|
В задании 10 вычислите криволинейный интеграл.
| ||
|
10.
|
10.
| |
|
Вариант 27 |
Вариант 28
| |
| ||
|
|
| |
|
В заданиях 2- 5 вычислите интегралы
| ||
|
2.
|
2.
| |
|
3.
|
3.
| |
|
4.
|
4.
| |
|
5.
|
5.
| |
|
В заданиях 6, 7 вычислите площадь фигуры, ограниченной заданными линиями
| ||
|
6.
|
6.
| |
|
7.
|
7.
. | |
|
В заданиях 8, 9 вычислите объем тела, ограниченного данными поверхностями
| ||
|
8.
|
8.
| |
|
9. |
9. | |
|
В задании 10 вычислите криволинейный интеграл.
| ||
|
10.
|
10.
| |
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
,
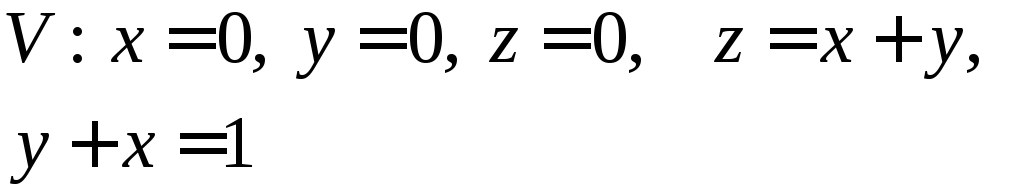
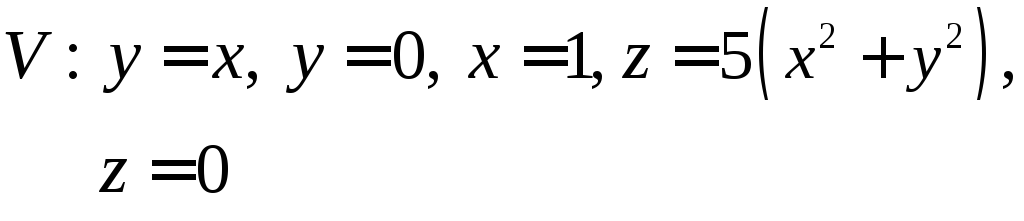