Двойные и криволинейные интегралы и их приложения.
ДВОЙНЫЕ ИНТЕГРАЛЫ
Пусть на квадрируемом множестве определена функция .
Под квадрируемым множеством подразумевается такое точечное множество D, которому можно по определенным правилам сопоставить некоторое неотрицательное число, являющееся его площадью.
Разобьем D
произвольными
кривыми на n
частей
.
Пусть
- площади этих частей, а
- их диаметры.
Напомним, что диаметром множества называется супремум расстояний между любыми двумя точками, принадлежащими данному множеству.
В каждой из
(
)
выберем произвольную точку
и составим интегральную
сумму
для функции
на множестве D.
Число
называется рангом
разбиения D.
Если существует
конечный предел
,
который не зависит ни от способа разбиения
D
на части, ни от выбора точек
,
то J
называется двойным
интегралом функции
по множеству
D
и обозначается
;
функция
в этом случае называется интегрируемой
на множестве
D.
Заметим, что функция , непрерывная на замкнутом квадрируемом множестве D, интегрируема на D.
Свойства двойных интегралов
Пусть функции
и
интегрируемы на множестве D.
Линейность интеграла. Для любых постоянных чисел
и
функция
+ интегрируема на D и верно равенство
=
+
.
Аддитивность по множеству. Если D некоторой непрерывной кривой L разбита на два множества D1 и D2 (
,
),
то функция
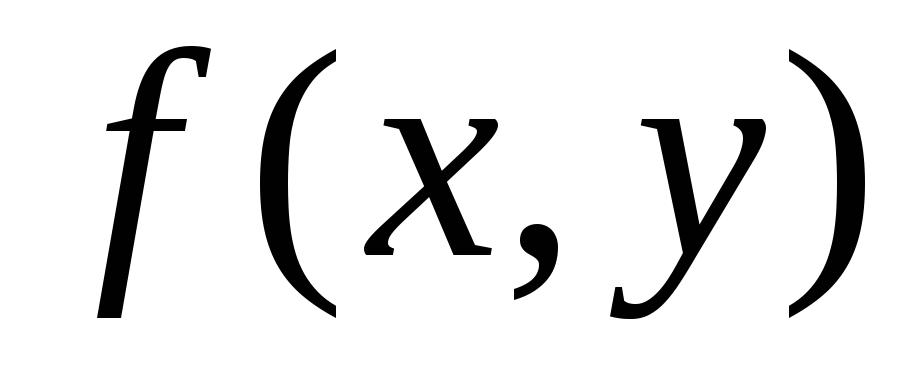интегрируема на D1
и D2
и
=
+
.
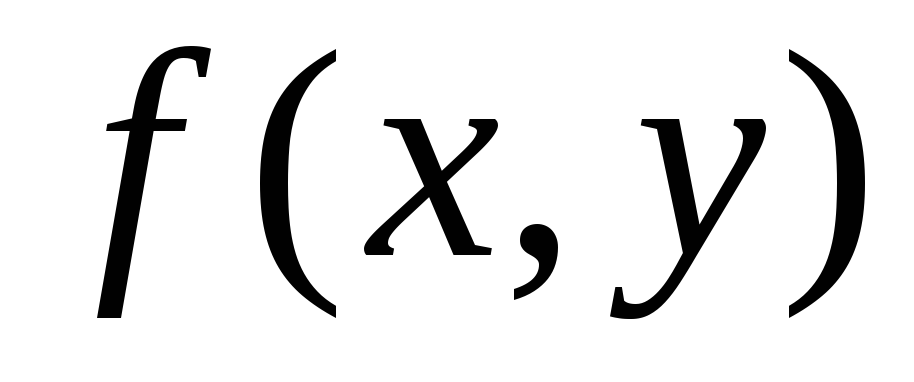
Монотонность. Если 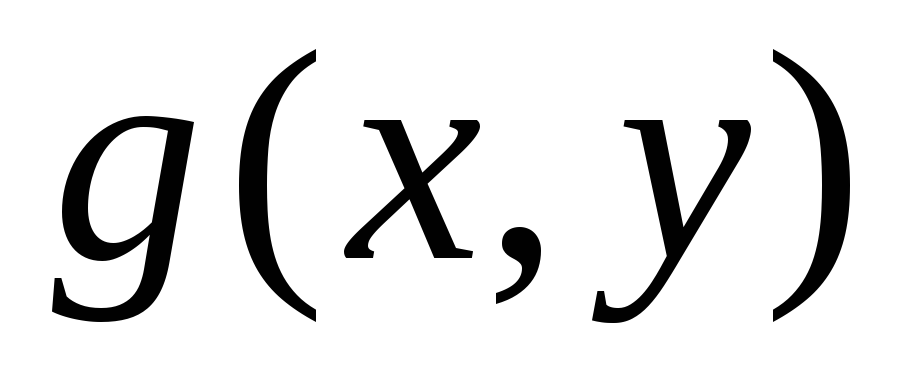для всех
,
то
.
Теорема о среднем значении. Пусть определена и непрерывна на связном, замкнутом и ограниченном множестве D.
Напомним, что множество называется связным, если любые две его точки можно соединить непрерывной кривой, целиком лежащей в этом множестве.
Тогда
существует такая точка
,
что
,
где P - площадь множества D.
Вычисление двойных интегралов
Множество
вида
,
где
- функции, непрерывные на a,b
,
на a,b,
называется элементарным
относительно
оси y.
Аналогично,
множество
,
где
- функции, непрерывные на c,d,
на c,d,
называется элементарным
относительно оси x.
Теорема (о вычислении двойного интеграла повторным интегрированием).
1). Пусть функция
интегрируема на множестве D,
элементарном относительно оси y,
и при каждом постоянном значении x
из a,b
существует интеграл
,
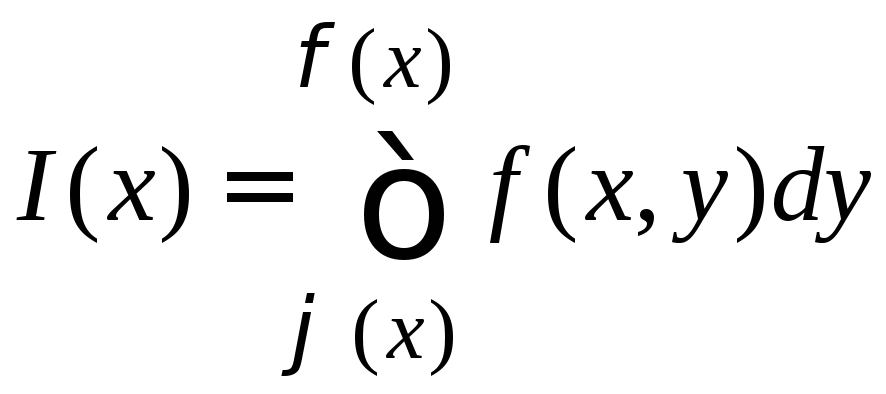тогда существует также интеграл
,
который называется повторным
интегралом,
и выполняется равенство
.
2). Аналогично, если
функция
интегрируема на множестве D,
элементарном относительно оси x,
и при каждом постоянном значении y
из c,d
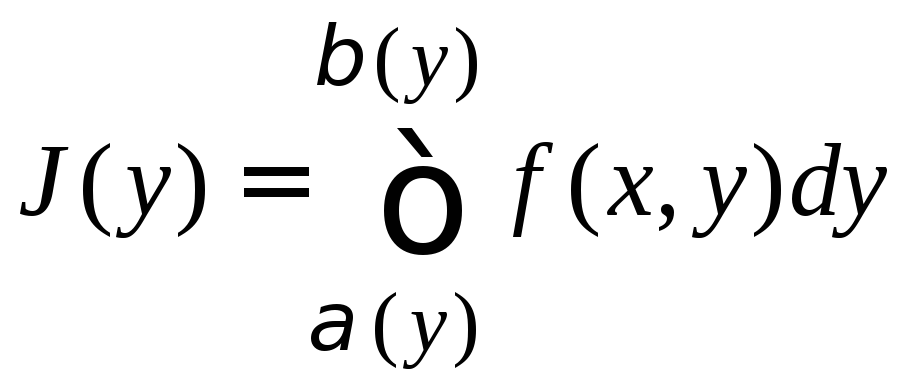существует интеграл
,
то существует интеграл
,
и выполняется равенство
.
П
ример
16. Вычислим
,
где D
- область,
ограниченная кривыми
и
(рис. 6).
Решая систему
,
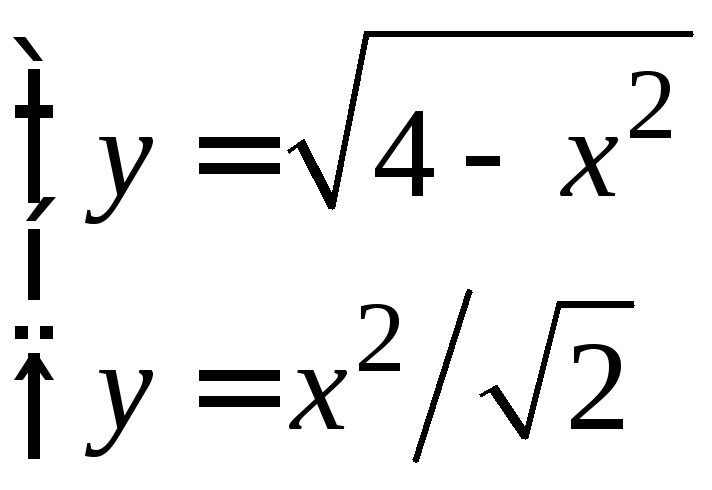найдем абсциссы точек пересечения
п
олуокружности
и параболы:
.
Заметим, что множество D
элементарно относительно оси y:
оно задается с помощью неравенств Рис. 6.
,
.
Поэтому двойной интеграл может быть вычислен повторным интегрированием:
=
=
=
.
Пример
17. Изменим
порядок интегрирования в повторном
интеграле
.
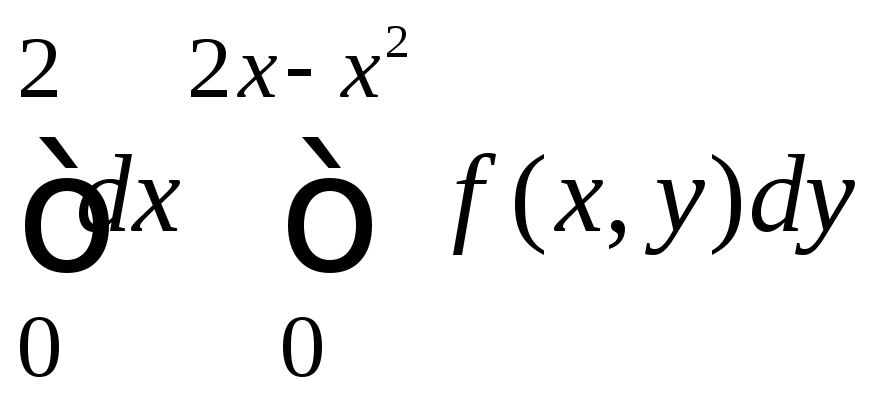Эта задача несколько сложнее предыдущей. Здесь не дана непосредственно область интегрирования, мы должны выяснить ее вид по пределам данного повторного интеграла.
Н
еравенства
,
задают множество D, которое изображено
на рис. 7. Проекцией D на ось y является
отрезок
.
Каждая прямая y=c
(c = const ) пересекает D по отрезку
,
где
и
являются
р
ешениями
уравнения
.
Решая последнее уравнение, находим
,
.
Рис. 7
Таким образом,
множество D
является элементарным относительно
оси x
и задается неравенствами
,
.
Поэтому
=
.
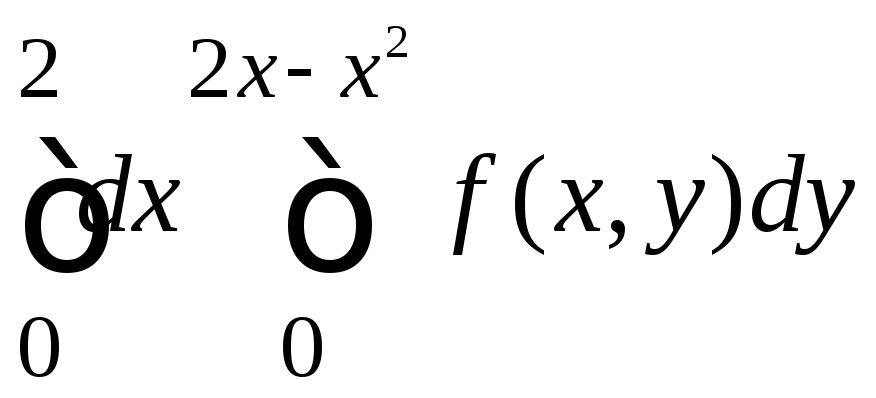Пример 18
.
Изменим порядок интегрирования в
повторном интеграле
.
y
Пределы интегрирования в
исходном интеграле показывают,
что область интегрирования D
задается неравенствами ,
.
Область D
изображена на рис. 8 (кривая
является
верхней
x
полуокружностью окружности
).
Легко увидеть,
Рис. 8
что множество D не является
элементарным
относительно оси x,
но его можно разбить на три множества
и
,
каждое из которых элементарно
относительно оси x
(см. рис.8).
Разрешая уравнения
и
относительно x,
получим соответственно
и
.
Таким образом, множество
может быть задано неравенствами
,
;
множество
может быть задано неравенствами
,
;
а множество
- неравенствами
,
.
Следовательно,
+
+
=
.
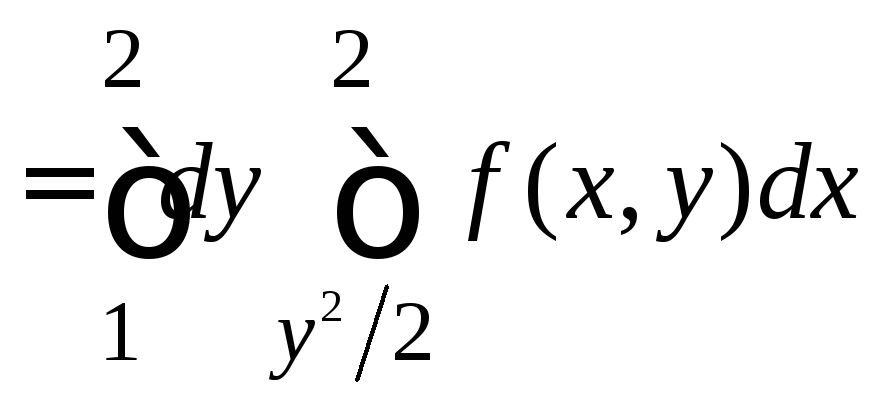