
Sb96728
.pdf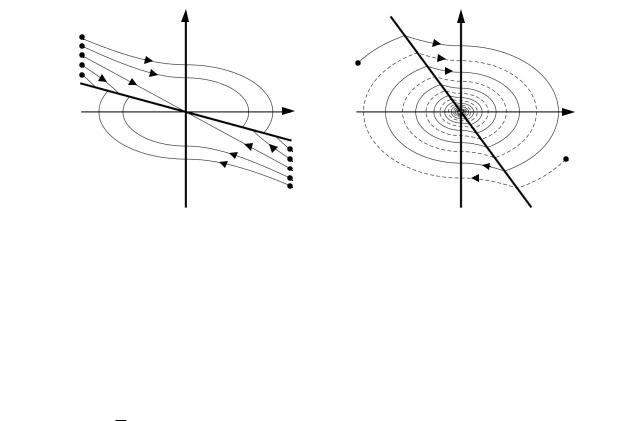
y |
y |
x |
x |
– x
– x
а |
б |
Рис. 6.3. Фазовые траектории системы с переменной структурой: а – со скользящим режимом; б – без скользящего режима
Как видно из фазовых траекторий рис. 6.3, движение изображающей точки в идеальном случае происходит с одним переключением, после чего наблюдается скольжение вдоль прямой линии x к началу координат. Во втором случае скольжения не наблюдается. Это вызвано тем, что угол наклона линии переключения больше угла наклона сепаратрисы седловой траектории, т. е. 
 k .
k .
6.2. Порядок выполнения работы
1.Создать новую модель в Matlab Simulink: New Simulink Model.
2.Во вкладке Configuration Parameters/Solver задать настройки расчета переходных процессов type – fixed step; step size – 1e–4.
3.Собрать модель системы с переменной структурой с объектом управления (6.1) и двумя регуляторами, обеспечивающими движение изображающей точки по эллипсу в соответствии с алгоритмом (6.2). Коэффициент k объекта управления (6.1) выбрать по таблице вариантов. Коэффициенты k1 и
k2 подобрать самостоятельно, чтобы получить асимптотическую устойчивость, причем необходимо выполнить неравенство k2>k1>0.
4.Исследовать движение фазовых координат во времени посредством моделирования процессов в системе при ее отклонении от состояния равновесия. Для этого в окне Function Block Parametrs интеграторов задать различные начальные значения (Initial condition).
5.Построить фазовые траектории и переходные процессы в системе.
6.Собрать модель системы с переменной структурой с объектом управления (6.1) и двумя регуляторами, обеспечивающими движение изображаю-
21

щей точки по отрезкам эллипсов и седловидных кривых в соответствии с алгоритмом (6.3). Коэффициент k объекта управления (6.1) выбрать по таблице вариантов. Задать начальные условия в интеграторах. Коэффициент k1 подобрать самостоятельно, чтобы получить асимптотическую устойчивость.
7. Исследовать движение фазовых координат во времени посредством моделирования процессов в системе при ее отклонении от состояния равновесия для двух вариантов алгоритма (6.3). Первый вариант – система со скользящим режимом, т. е. 0 
 k . Второй вариант – система без скользящего режима, т. е.
k . Второй вариант – система без скользящего режима, т. е. 
 k .
k .
8.Построить фазовые траектории и переходные процессы в системе.
9.Сделать выводы об изменениях фазовых траекторий рассмотренных систем.
Вариант |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
k |
1,5 |
2,5 |
3,5 |
4,5 |
1 |
1 |
2 |
3 |
4 |
5 |
Содержание отчета
1.Титульный лист.
2.Цель работы.
3.Математическое описание объекта и закона управления. Расчетные схемы согласно варианту, выполненные в Matlab Simulink.
4.Графики переходных процессов и фазовых траекторий.
5.Выводы по исследованию различных систем с переменной структурой.
Контрольные вопросы
1.Что такое система с переменной структурой? Принципы формирования систем с переменной структурой?
2.Дайте определение устойчивости системы. Укажите основные типы устойчивости.
3.Типы фазовых траекторий линейной системы второго порядка.
4.Что такое скользящий режим? Укажите условия возникновения и существования скользящего режима в системе.
5.Перечислите основные правила построения фазовых траекторий. Что такое линия переключения в системе с переменной структурой?
22
Лабораторная работа 7. ИССЛЕДОВАНИЕ НЕЛИНЕЙНОЙ СИСТЕМЫ С ЧАСТОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИЕЙ
Цель работы – исследование реакции нелинейной импульсной системы на изменение параметров частотно-импульсного модулятора.
7.1. Общие сведения
По виду модуляции все импульсные системы делятся на амплитудноимпульсные, широтно-импульсные, частотно-импульсные и т. д. Основные достоинства импульсных систем автоматического управления обусловлены прерывистым характером передачи сигналов между отдельными частями системы и состоят в возможности многоточечного управления, многократного использования линий связи, а также повышенной помехозащищенности.
Первое достоинство заключается в том, что с помощью одного управляющего устройства импульсного действия можно управлять несколькими объектами посредством циклического подключения этого управляющего устройства последовательно к каждому из объектов. Время между двумя очередными импульсами, поступающими на один объект, используется для обмена дискретными сигналами с остальными объектами. Возможность многократного использования одного канала связи для управления несколькими объектами, удаленными от места нахождения управляющих устройств импульсного действия, основана на том же принципе последовательного соединения объектов и соответствующих управляющих устройств линий связи с помощью синхронно действующих на концах линии шаговых распределителей.
Повышенная помехозащищенность импульсных систем обусловлена возможностью передавать информацию в виде очень коротких импульсов, в промежутки между которыми система оказывается разомкнутой и не реагирует на внешние возмущения.
Частотно-импульсная модуляция (ЧИМ) – это способ формирования импульсных сигналов в системах управления, состоящий в изменении частоты следования импульсов при неизменных длительности и амплитуды импульса. При этом частота следования импульсов понимается как мгновенная частота синусоидальных частотно-модулированных колебаний, у которых фазовые значения n 0 2 n , где 0 const, n 1, 2, ..., совпадают по времени с моментами появления импульсов.
23
Структурная схема одного из вариантов реализации двухполярного ча- стотно-импульсного модулятора представляет собой последовательное соединение интегрирующего звена, нелинейного элемента квантования приращений НК и формирователя прямоугольных импульсов с передаточной функцией
|
|
|
|
|
W |
p 1 e p |
|
|
|
|
||
|
|
|
|
|
ф |
|
|
|
|
|
|
|
и приведена на рис. 7.1 а. |
|
|
|
|
|
|
|
|||||
x |
1/p |
x1 |
НК |
x2 |
Wф(p) |
y |
|
x |
ЧИМ |
y |
Wл(p) |
z |
|
|
|
|
|
|
|
|
|||||
|
|
|
а |
|
|
|
|
|
|
|
б |
|
|
|
|
|
|
|
|
|
|
|
|
||
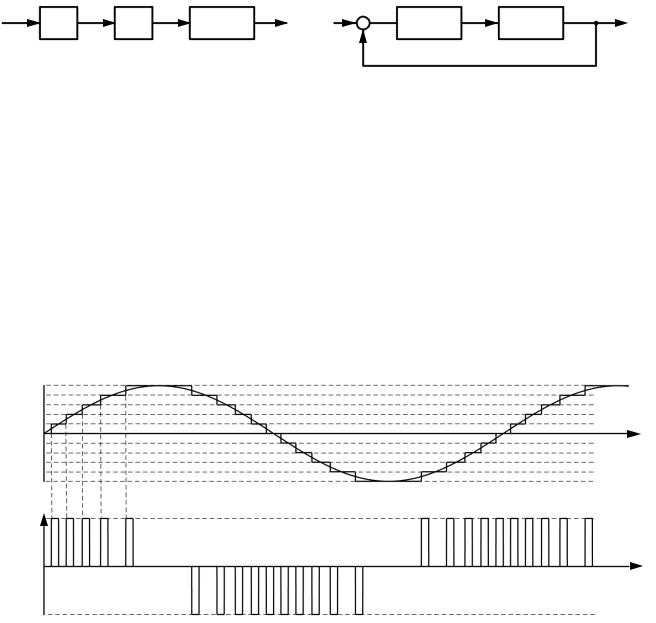
Рис. 7.1. Структурные схемы:
а – частотно-импульсного модулятора; б – импульсной следящей системы
Принцип работы частотно-импульсного модулятора, структурная схема которого представлена на рис. 7.1 а, заключается в следующем: на первом этапе происходит квантование входного сигнала по уровню , на втором этапе – формирование прямоугольных импульсов с заданной длительностью , амплитудой и переменной частотой, соответствующей частоте изменения уровней квантованного сигнала. В качестве примера на рис. 7.2 приведен график на выходе частотно-импульсного модулятора при синусоидальном входном сигнале.
x
5 
– |
t |
–5
y
t
–
Рис. 7.2. Принцип формирования частотно-импульсной модуляции
Квантование по уровню также можно реализовать как с использованием обычного элемента квантования приращений уровня (рис. 7.3, а), так и элемента квантования приращений уровня с гистерезисом (рис. 7.3, б).
24

x2 |
|
|
x2 |
|
|
|
|
|
x1 |
|
|
x1 |
|
– |
– |
|||||
– |
|
– |
|
|||
|
|
|
|
|||
а |
|
|
б |
|
|
Рис. 7.3. Графики статической характеристики нелинейного элемента квантования приращений: а – без гистерезиса; б – с гистерезисом
Количество нелинейных элементов, обладающих характеристикой типа гистерезис, определяется выражением n = 0.5(k + 1), где k = / – требуемое количество уровней квантованного сигнала.
Для исследования работы импульсных систем с ЧИМ предлагается рассмотреть систему, структурная схема которой представлена на рис. 7.1, б.
7.2. Порядок выполнения работы
1.Создать новую модель в Matlab Simulink: New Simulink Model.
2.Во вкладке Configuration Parameters/Solver задать настройки расчета переходных процессов type – fixed step; step size – 1e–4.
3. Собрать |
схему |
импульсной |
системы с ЧИМ в соответствии с |
|||
рис. 7.1, б; в качестве входного сигнала использовать элемент Sine Wave. |
||||||
4. Исследовать влияние на работу системы варьирование параметра . |
||||||
|
|
|
|
|
|
|
Вариант |
|
Значения параметров |
Wл(p) |
|||
|
|
|
|
|
||
|
|
|
|
|
||
|
|
|
|
|||
1 |
|
10 |
|
2.0 |
0.10 |
10/(p + 0.1) |
2 |
|
5 |
|
1.0 |
0.05 |
7/(p2 + 0.25p + 1) |
3 |
|
12 |
|
0.5 |
0.01 |
6/(p2 + 0.1) |
4 |
|
3 |
|
1.0 |
0.10 |
100/(p2 + p) |
5 |
|
25 |
|
5.0 |
0.10 |
20/(p2 + p + 1) |
6 |
|
8 |
|
2.0 |
0.10 |
15/(p + 1) |
7 |
|
2 |
|
0.5 |
0.10 |
11/(p + 0.5) |
8 |
|
3 |
|
0.6 |
0.01 |
9/(p2 + 0.9) |
9 |
|
18 |
|
6.0 |
0.01 |
90/(p2 + p) |
10 |
|
8 |
|
2.0 |
0.10 |
8/(p2 + 0.09p + 1) |
Содержание отчета
1.Титульный лист.
2.Цель работы.
3.Расчетные схемы согласно варианту, выполненные в Matlab Simulink.
4.Осциллограммы исследуемых переменных.
25
5. Выводы по исследованию реакции импульсной системы на изменение параметров частотно-импульсного модулятора.
Контрольные вопросы
1.Дайте определение ЧИМ.
2.Опишите принцип работы частотно-импульсного модулятора.
3.Регулирование каких параметров частотно-импульсного модулятора оказывает влияние на качество выходного сигнала импульсной системы с ЧИМ?
4.Какую форму принимает входной сигнал на выходе частотноимпульсного модулятора?
5.Приведите примеры применения импульсных систем с ЧИМ.
Лабораторная работа 8. ИССЛЕДОВАНИЕ ИМПУЛЬСНОЙ СИСТЕМЫ С ШИРОТНО-ИМПУЛЬСНОЙ МОДУЛЯЦИЕЙ
Цель работы – исследование реакции импульсной системы на изменение параметров широтно-импульсного модулятора.
8.1. Общие сведения
Широтно-импульсная модуляция (ШИМ) – это способ формирования импульсных сигналов в системах управления, состоящий в изменении длительности при неизменной частоте следования импульса. В зависимости от реализации ШИМ можно разделить на аналоговый и цифровой.
Вработе рассмотрен пример применения ШИМ-генератора аналогового типа для решения задачи стабилизации тока, протекающего через активноиндуктивную нагрузку.
ВШИМ-генераторах аналогового типа, управляющий сигнал формируется аналоговым компаратором, когда на инвертирующий вход компаратора подается треугольный или пилообразный сигнал («пила»), называемый также опорным, а на неинвертирующий – модулирующий непрерывный сигнал.
Выходные импульсы ШИМ-модулятора имеют прямоугольную форму, частота их следования равна частоте «пилы». Длительность импульса зависит от времени, в течение которого уровень модулирующего сигнала превышает уровень «пилы». В случае, когда уровень «пилы» выше уровня модулирующего сигнала, на выходе будет нулевая часть импульса.
26
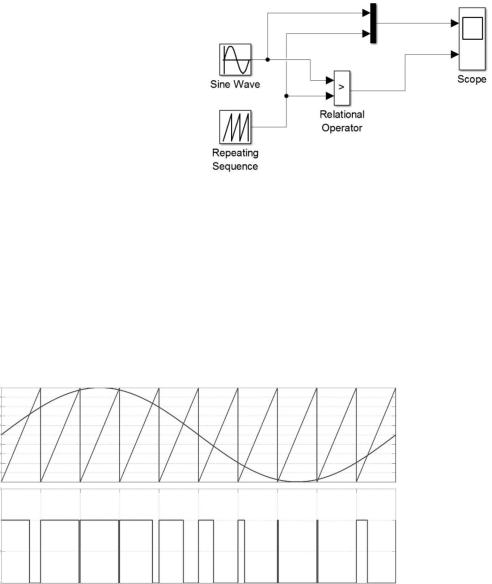
Для получения первого представления о принципе работы ШИМ, необходимо в программной среде Matlab Simulink собрать схему, изображенную на рис. 8.1. Для наглядности аналоговый компаратор заменяется блоком
сравнения Relational Operator библиотеки Similink/Logical Operations, в кото-
ром верхний вход эквивалентен неинвертирующему входу аналогового компаратора, а нижний, соответственно, инвертирующему. На входы блока Relational Operator поступают:
–модулирующий сигнал синусоидальной формы с блока Sine Wave;
–опорный сигнал пилообразной формы с блока Repeating Sequence. Результаты моделирования схемы получения ШИМ-сигнала приведены
на рис. 8.2.
Рассмотрим работу ШИМ-генератора на примере модели импульсного стабилизатора тока.
Uвх,
В
0.0
Uвых,
В
0.0
0.0 |
t, c |
|
Рис. 8.2. Результаты моделирования схемы ШИМ
На практике этот вид стабилизаторов часто применяется в системах заряда аккумуляторных батарей для ограничения зарядного тока, а также для ликвидации токового броска при подключении емкостной нагрузки к источнику постоянного напряжения. Как правило, для управления током нагрузки применяется единственный силовой ключ (IGBT-модуль), управляемый ШИМ-генератором. Модель стабилизатора тока в Matlab Simulink приведена на рис. 8.3.
27
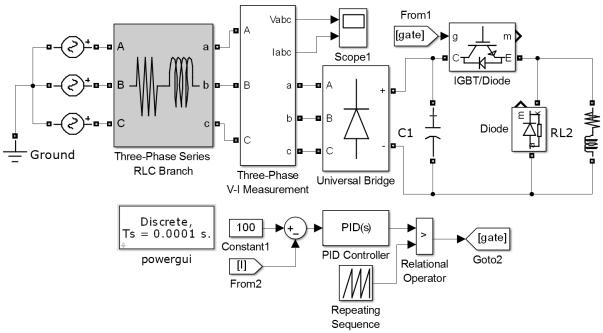
Рис. 8.3. Модель стабилизатора тока в Matlab Simulink
Импульсный стабилизатор тока в данном случае работает на активноиндуктивную нагрузку и имеет обратную связь по току нагрузки. Управление силовым ключом осуществляется сигналом gate. Подстройкой ПИДрегулятора обеспечивается заданные показатели качества регулирования тока нагрузки.
8.2. Порядок выполнения работы
1.Создать новую модель в Matlab Simulink: New Simulink Model.
2.Во вкладке Configuration Parameters/Solver задать настройки расчета переходных процессов type – fixed step; step size – 1e–4.
3.Для обеспечения работы модели добавить блок powergui с параметра-
ми Simulation time – Discrete; Solver type – Tustin; Sample time – 1e–4.
4.Собрать схему импульсного стабилизатора тока, задать параметры сети, опорного сигнала («пилы»). Задания тока и нагрузки выбрать по таблице вариантов.
5.Подобрать параметры ПИД-регулятора таким образом, чтобы в модели обеспечивалась стабилизация заданного значения тока. Полученные в блоке Scope графики и параметры ПИД-регулятора привести в отчете.
6.Исследовать влияние частоты опорного сигнала на качество стабилизации тока.
28
|
Lвх, |
Rвх, |
С1, |
|
Параметры нагрузки |
|
Параметры опор- |
|||
Вариант |
Uвх, В |
Iз, А |
ного сигнала |
|||||||
мГн |
Ом |
мФ |
|
|
||||||
|
|
Rн, Ом |
Lн, мГн |
|
Uоп, В |
fоп, кГц |
||||
|
|
|
|
|
|
|||||
1 |
2 |
0.01 |
7 |
100 |
0.01 |
10 |
100 |
1.0 |
1.0 |
|
2 |
2 |
0.01 |
7 |
120 |
0.15 |
11 |
110 |
1.5 |
1.1 |
|
3 |
2 |
0.01 |
7 |
140 |
0.20 |
9 |
120 |
1.2 |
1.6 |
|
4 |
2 |
0.01 |
7 |
160 |
0.07 |
8 |
130 |
3.0 |
1.5 |
|
5 |
2 |
0.01 |
7 |
180 |
0.13 |
7 |
140 |
1.5 |
1.4 |
|
6 |
2 |
0.01 |
7 |
200 |
0.10 |
12 |
150 |
1.5 |
1.3 |
|
7 |
2 |
0.01 |
7 |
180 |
0.13 |
13 |
160 |
2.0 |
1.7 |
|
8 |
2 |
0.01 |
7 |
160 |
0.18 |
14 |
170 |
2.5 |
1.9 |
|
9 |
2 |
0.01 |
7 |
130 |
0.09 |
15 |
180 |
1.8 |
2.5 |
|
10 |
2 |
0.01 |
7 |
100 |
0.11 |
10 |
190 |
2.5 |
2.0 |
|
Содержание отчета
1.Титульный лист.
2.Цель работы.
3.Расчетные схемы согласно варианту, выполненные в Matlab Simulink.
4.Осциллограммы исследуемых переменных.
5.Выводы по исследованию реакции импульсной системы на изменение параметров широтно-импульсного модулятора.
Контрольные вопросы
1.Дайте определение ШИМ.
2.Опишите алгоритм формирования синусоидального ШИМ-сигнала.
3.Что представляет собой импульсный стабилизатор тока? Перечислите основные функции.
4.Перечислите основные способы поддержания качества стабилизированного тока.
5.В чем заключаются опасности работы IGBT-модуля?
29
СПИСОК РЕКОМЕНДУЕМОЙ ЛИТЕРАТУРЫ
Афанасьев В. Н. Математическая теория конструирования систем управления: учеб. пособие. 3-е изд., испр. и доп. М.: Высш. шк., 2004.
Бесекерский В. А., Попов Е. И. Теория систем автоматического управления. 4-е изд., перераб. и доп. СПб.: Профессия, 2003.
Зайцев Г. Ф., Стеклов В. К. Компенсация естественных нелинейностей автоматических систем. М.: Энергоатомиздат, 1982.
Математические основы теории автоматического управления: учебник в 3 т. Т. 1, 3-е изд., перераб. и доп. / под ред. Б. К. Чемоданова. М.: Изд-во МГТУ им. Н. Э. Баумана, 2006.
Математические модели, динамические характеристики и анализ систем автоматического управления // Методы классической и современной теории автоматического управления: учебник в 5 т. Т. 1, 2-е изд., перераб. и доп. / под ред. К. А. Пупкова, Н. Д. Егупова. М.: Изд-во МГТУ им. Н. Э. Баумана, 2004.
Мирошник И. В. Теория автоматического управления. Нелинейные и оптимальные системы. СПб.: Питер, 2006.
Пальтов И. П. Нелинейные методы исследования автоматических систем. Л.: Энергия, 1976.
Пальтов И. П., Попов Е. П. Приближенные методы исследования нелинейных автоматических систем. М.: Физ.-мат. лит., 1960.
Первозванский А. А. Курс теории автоматического управления: учеб. пособие. М.: Наука, 1986.
Петров В. В., Гордеев А. А. Нелинейные сервомеханизмы. М.: Машиностроение, 1979.
Попов Е. П. Прикладная теория процессов управления в нелинейных системах. М.: Наука, 1973.
Теория автоматического управления: учебник для вузов по спец. «Автоматика и телемеханика»: в 2 ч. Ч. II. Теория нелинейных и специальных систем автоматического управления / под ред. А. А. Воронова. М.: Высш. шк.,
1986.
Юревич Е. И. Теория автоматического управления. М.: Энергия, 1969.
30
