
Sb95841
.pdf
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)
С. В. ВОРОБЬЕВ О. П. КОРМИЛИЦЫН
ПЕРЕМЕЩЕНИЯ И АНАЛИЗ СТАТИЧЕСКИ НЕОПРЕДЕЛИМЫХ СИСТЕМ
Учебно-методическое пособие
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2017
УДК 539.3 (07)
ББК В251.62я7 В75
Воробьев С. В., Кормилицын О. П.
В75 Перемещения и анализ статически неопределимых систем: учеб.-метод. пособие. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2017. 32 с.
ISBN 978-5-7629-2080-3
Рассмотрены методы расчета перемещений в стержне при различных видах деформаций. Представлены метод сил и метод перемещений для решения статически неопределимых задач. Расчет перемещений при изгибе показан на примере метода начальных параметров, теоремы Кастельяно и формулы Максвелла–Мора.
Дана необходимая информация о механических характеристиках материалов.
Предназначено для использования в курсе прикладной механики студентами технических факультетов дневной формы обучения. Может быть полезно студентам очно-заочной формы обучения.
УДК 539.3 (07)
ББК В251.62я7
Рецензент: канд. техн. наук И. В. Штурц (СПбГПУ).
Утверждено редакционно-издательским советом университета
в качестве учебно-методического пособия
ISBN 978-5-7629-2080-3 |
© СПбГЭТУ «ЛЭТИ», 2017 |
2
Статически неопределимыми называют конструкции, в которых для определения опорных реакций либо внутренних усилий одних только уравнений статики недостаточно, а требуется совместное рассмотрение последних с дополнительными уравнениями, характеризующими деформации системы.
Статическая неопределимость возникает из-за наличия дополнительных связей – дополнительных опор, добавление которых не влияет на геометрическую неизменяемость системы в целом. Дополнительные опоры позволяют увеличить прочность и жесткость конструкций.
Известны два основных метода расчета статически неопределимых систем – метод перемещений и метод сил. В первом за лишние неизвестные принимаются перемещения, во втором – силы.
Метод уравнивания перемещений базируется на определении перемещений при различных видах деформации.
Рассмотрим основные способы определения перемещений.
1.РАСЧЕТ ПЕРЕМЕЩЕНИЙ
1.1.Метод начальных параметров
При расчете элементов конструкции электронной техники следует также проводить анализ жесткости как конструкции в целом, так и ее отдельных элементов.
Для количественной оценки жесткости конструкции следует определить упругие перемещения элементов конструкции под воздействием внешних нагрузок. Определение перемещений необходимо также при исследовании вопросов колебаний упругих систем.
Для элементов конструкции электронной техники, которые могут быть представлены в виде стержневой расчетной схемы, наибольший интерес представляет определение перемещения оси стержня в плоскости нагружения при чистом или плоском поперечном изгибе.
Приближенное дифференциальное уравнение изогнутой оси стержня имеет вид
d 2u |
z |
|
M y |
, |
(1.1) |
|
|
|
|||
dx2 |
EJ y |
|
|
||
где uz – компонента вектора перемещения в направлении оси z (рис. 1.1).
3
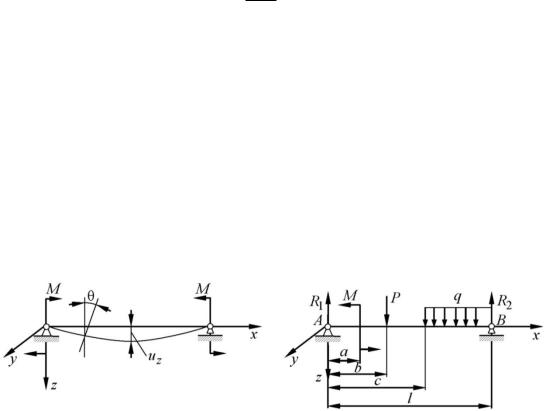
Угол поворота сечений связывается с прогибом зависимостью
dudxz θ,
при этом используется допущение о малости угла θ = tg θ.
Если жесткость поперечного сечения при изгибе EJ y постоянна по дли-
не стержня, то прогибы оси и угла поворота различных поперечных сечений могут быть получены непосредственным интегрированием уравнения (1.1) или интегрированием по методу начальных параметров.
Метод начальных параметров удобно использовать при наличии нескольких нагрузок (рис. 1.1), так как при любом числе грузовых участков нужно определить всего две произвольные постоянные интегрирования: прогиб uz0 и угол поворота θ0 в начале координат.
Рис. 1.1 Рис. 1.2
Уравнения метода начальных параметров имеют вид |
|
|
|||||||||||||||||
|
|
|
|
|
Mi (x a) |
|
|
|
Pi (x b)2 |
|
gk (x c)3 |
|
|
||||||
|
|
|
|
|
|
i |
|
|
|
j |
|
|
|
k |
|
, |
|
||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
uz θ uz |
0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
EJ y |
|
|
|
|
|
2EJ y |
|
|
6EJ y |
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
Mi (x a)2 |
|
|
|
Pi (x b)3 |
|
|
gk (x c)4 |
|
|||||
|
|
|
|
|
|
i |
|
|
|
|
|
j |
|
|
k |
|
|
||
uz uz |
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
. |
||||
uz |
|
|
|
|
|
|
|
|
|
|
|
||||||||
0 |
0 |
|
|
|
2EJ y |
|
|
|
|
|
6EJ y |
|
|
24EJ y |
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
При использовании этих уравнений нужно соблюдать следующие условия:
–начало координат помещается в крайнюю левую точку оси стержня;
–знак «плюс» в уравнениях соответствует положительному направлению сил и моментов;
–a, b, c – расстояния от начала координат до точки приложения соответствующей нагрузки (для распределенной нагрузки – до начала участка, где она действует);
–под знак суммирования включаются только те нагрузки, которые лежат левее рассматриваемого сечения;
4
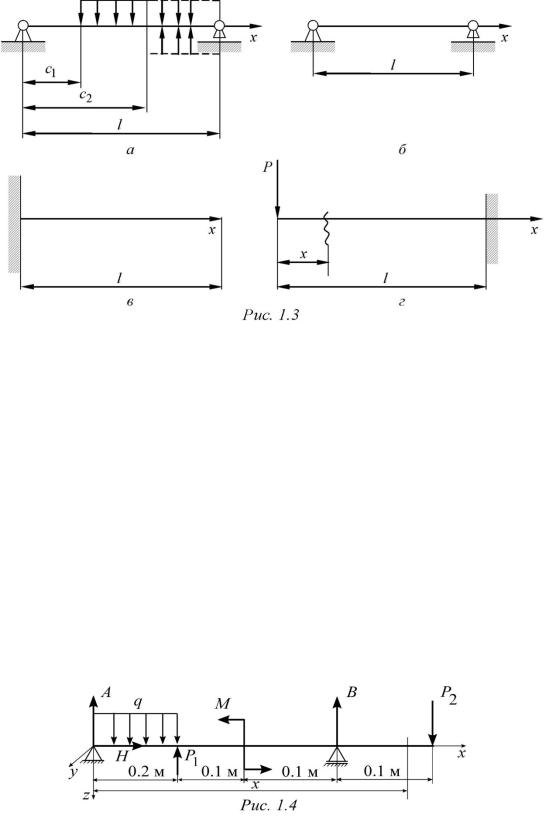
– если распределенная нагрузка заканчивается ранее сечения, где определяются прогиб и угол поворота, то она должна быть продолжена до указанного сечения и при этом следует добавить к ней нагрузку той же интенсивности, но противоположного знака (рис. 1.3, а).
|
θ0 и прогиб uz |
в начале балки определяются из гра- |
Угол поворота uz |
||
0 |
|
0 |
ничных условий, которые для наиболее распространенных случаев закрепления могут быть записаны следующим образом (рис. 1.3, б–г):
uz 0 uz0 0, |
uz l 0; |
||
uz 0 uz0 0, |
|
|
0; |
uz 0 uz0 |
|||
uz l 0, |
|
|
|
uz l 0. |
|
||
Пример 1.1. Рассмотрим конструкцию, расчетная схема которой представлена на рис. 1.4. На стержень, опертый на две опоры, действуют внешние воздей-
ствия: q 100 H/м, |
P 10 Н, |
M 1 Н м, |
P 20 H. Общая длина стержня |
|
1 |
|
2 |
L 5l 0.5 м. Жесткость стержня при изгибе |
EJ y const. Стержень имеет че- |
||
тыре грузовых участка.
5
Требуется определить линейное перемещение uzC сечения x = 0.3 м и угол поворота uzD D сечения x = 0.4 м.
Решение:
1.Проведем оси координат. Начало координат выберем в крайнем левом сечении, направим ось x вдоль оси стержня, ось z – вниз, а ось y – перпендикулярно плоскости чертежа так, чтобы система координатных осей стала правой.
2.Обозначим на схеме (рис. 1.4) реакции опор A, H, B.
3.Определим неизвестные внешние силы (реакции опор) из уравнений статического равновесия стержня:
Pix 0 H 0;
i
|
M |
A |
(P ) 0 q2l2 |
P 2l M B4l P 5l 0 B 20 H; |
|||
|
|
i |
|
1 |
2 |
||
i |
|
|
|
|
|
|
|
|
M |
B |
P |
0 A4l q2 / 3l P 2l M P l 0 A 10 Н. |
|||
|
i |
|
1 |
2 |
|||
i
4. Запишем выражения для определения прогиба и угла поворота произвольного сечения x стержня на четвертом участке:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
4 |
|
|
q |
|
|
x 2l |
|
4 |
|
|
P |
|
|
x 2l |
3 |
|
|||||||||||||
|
|
|
|
|
|
|
|
1 |
|
|
|
|
Ax |
|
|
|
|
|
|
qx |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
uz u0 0x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|||||||||||||||||||||
|
EJ |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
6 |
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
y |
|
6 |
|
|
|
|
|
|
|
24 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
M x 3l |
2 |
|
|
|
|
B x |
|
|
|
3 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
4l |
|
|
|
; |
|
|
|
|
|
|
|
|
|
|
|
|
(1.2) |
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
q |
|
|
x 2l |
|
3 |
|
|
|
|
|
P |
|
x 2l |
|
|
2 |
|
|
|
|||||||||||||
|
|
|
|
|
1 |
|
|
|
|
Ax |
|
|
|
|
qx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||||||
|
|
|
|
|
EJ |
|
|
|
|
|
|
2 |
|
|
6 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M x 3l |
|
B x |
|
4l |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
|
|
|
|
|
|
|
|
|
|
|
|
(1.3) |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Определим из граничных условий начальные параметры uz0 |
и 0 : |
||||||||||||||||||||||||||||||||||||||||||||||||||||||
а) uz |
|
|
|
x 0 0 |
uz0 0; |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
б) uz |
|
x 4l 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
6
|
|
1 |
|
A(4l)3 |
|
|
q(4l)4 |
|
q(2l)4 |
|
P (2l)3 |
|
Ml2 |
|
|
|||
|
0 4l |
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
0 |
EJ y |
6 |
|
|
24 |
|
|
|
24 |
|
6 |
|
2 |
|
|
||
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1.71 |
. |
|
|
|
|
|
|
|
|
||
|
|
|
|
0 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
EJ y |
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
5. Определим перемещения uzC и D . Воспользуемся формулами (1.2) и (1.3). Окончательно получим:
uzC |
0.515 |
, |
D |
2.260 |
. |
|
|
||||
|
EJ y |
|
EJ y |
||
1.2. Энергетические методы определения перемещения
1.2.1. Работа силы. Понятие об обобщенной силе и обобщенном перемещении
Работа А постоянной по значению силы Р, совершаемая ею на упругом перемещении δ точки ее приложения, равна скалярному произведению векторов силы Р и перемещения δ:
А (P, δ).
Если сила Р изменяется вместе с δ и между ними существует определенная зависимость P(t) f δ(t) , то работа, совершаемая этой силой, может
быть найдена следующим образом. Рассматриваем два близких момента времени. В первом из них имеем P(t) и δ(t) , а во втором – P(t) dP(t) и δ(t) dδ(t) . Работа, совершаемая силой за отрезок времени между этими моментами, равна
dA P(t)dδ(t).
Работа, совершаемая силой dP(t) на перемещении dδ(t) , является величиной второго порядка малости, и ею можно пренебречь. Отсюда
δ |
δ |
A P(t) dδ(t) f δ(t) dδ(t) . |
|
0 |
0 |
Если зависимость между силой и перемещением линейная, т. е. P(t)αδ(t) , и, в частности, в конце роста силы P αδ , то работа А представляется в виде
δ |
αδ |
2 |
|
1 |
|
A αδ(t) dδ(t) |
|
|
Pδ. |
||
2 |
|
2 |
|||
0 |
|
|
|
||
|
|
|
|
|
7
Введем понятие обобщенной силы и обобщенного перемещения. Любая система уравновешенных сил есть обобщенная сила. Перемещение в направлении обобщенной силы есть обобщенное перемещение.
1.2.2. Потенциальная энергия твердого тела
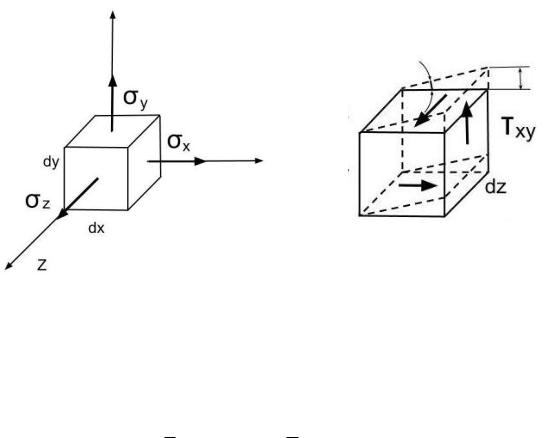
Потенциальная энергия деформации, если не учитывать потери, равна работе силы на перемещение. В твердом деформированном теле в окрестности точки, где известны составляющие напряжений, выделим бесконечно малый элемент в виде куба с ребрами dx, dy, dz.
На рис. 1.5, а показаны нормальные составляющие напряжений, на рис. 1.5, б – касательные составляющие напряжений, действующие на выделенный элемент.
y
yxy
а
|
|
|
|
|
|
|
|
ζ y |
|
|
|
|
|
|
|
|
η |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
η yz |
|
|
|
xy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ζx |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
dy |
|
|
|
|
|
|
x |
dy |
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
ζz |
|
|
|
|
dz |
|
|
|
dz |
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
ηzx |
|
|
||||||||
|
|
|
|
|
|
dx |
|
|
dx |
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
а |
|
б |
|
|
||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||
Рис. 4.4 Рис. 1.5
В соответствии с принципом (независимость действия сил) работа (потенциальная энергия деформации) сил, действующих на грани dy dz выделенного элемента, равна:
12 ζx dy dz dx 12 ηxy dy dz a,
где ζx dy dz – сила, действующая на грани dy dz выделяемого элемента в направлении оси координат x; dx – удлинение элемента в направлении оси координат x (перемещение); ηxy dy dz – сила, действующая по касательной к грани dy dz выделенного элемента; a – сдвиг грани (перемещение).
8
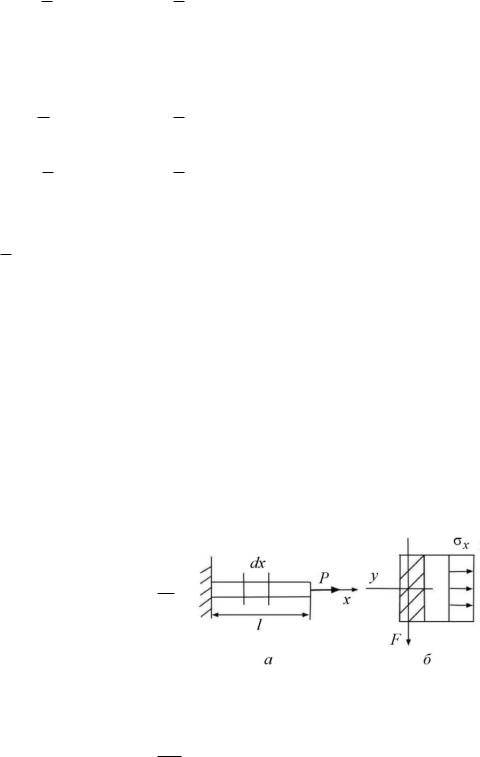
Учитывая, что |
εx |
dx |
, |
tg γxy |
a |
γxy (ввиду малости угла сдвига), |
|
dx |
dx |
||||||
|
|
|
|
|
потенциальная энергия деформации от сил, действующих на грани dy dz выделенного элемента, может быть записана как
12 ζx dx dy dz εx 12 ηxy dx dy dz γxy.
Аналогично потенциальная энергия деформации запишется от сил, действующих на гранях dx dz и dx dy выделенного элемента:
12 ζ y dx dy dz ε y 12 η yz dx dy dz γ yz ,
12 ζz dx dy dz εz 12 ηzx dx dy dz γzx.
Потенциальная энергия деформации единицы выделенного объема равна
U0 12 ζxεx ζ yε y ζzεz ηxyγxy η yzγ yz ηzxγzx .
В полученное уравнение потенциальной энергии деформации вместо линейных и угловых деформаций подставим их выражения из закона Гука. В результате получим:
|
|
1 |
2 |
2 2 |
|
|
1 |
2 |
2 |
2 |
|
U0 |
|
|
ζx |
ζ y ζz |
2ν ζxζ y ζ yζz ζzζx |
|
|
ηxy η yz ηzx . |
|||
2E |
2G |
||||||||||
|
|
|
|
|
|
|
|
|
|||
1.2.3. Потенциальная энергия стержня при различных видах деформации
На рис. 1.6, а показан стержень, испытывающий деформацию растяже- ния-сжатия. На рис. 1.6, б распределение составляющих напряжений ζx по сечению стержня. Выделим в стержне
элемент длиной dx.
При растяжении-сжатии ζx NF ,
отсюда потенциальная энергия деформации единицы выделенного объема стержня при деформации растяжениясжатия
ζ2
U0(N ) x
2E
Рис. 1.6
|
N 2 |
|
|
. |
|
2EF 2 |
||
9
Потенциальная энергия деформации элементарного объема стержня длиной dx
N 2dx Uax(N ) 2EF .
Потенциальная энергия деформации всего стержня длиною l
l N 2dx U N 0 2EF .
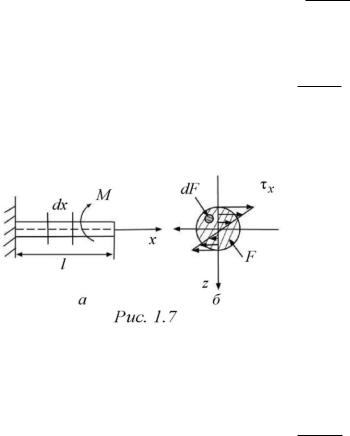
На рис. 1.7, а изображен стержень, испытывающий деформацию кручения; на рис. 1.7, б показано распределение действующих напряжений по сечению.
При деформации кручения полное касательное напряжение составляет
|
η |
x |
|
M x |
ρ. |
|
Рис. 1.7 |
||||||
|
||||||
|
|
Jρ |
||||
|
|
|
|
|||
|
|
|
|
|||
Потенциальная энергия деформации единицы объема, выделенного элемента стержня длиной dx ,
M 2 2 U0 M x x2 ρ .
2GJρ
Касательные напряжения, возникающие при кручении, изменяются по сечению стержня (рис. 1.7, б). Поэтому для расчета потенциальной энергии элементарного объема выделенного элемента необходимо в сечении выделить элементарную площадку dF и проинтегрировать полученное выражение потенциальной энергии по площади сечения F :
Uax M x |
M x2ρ2dx dF |
|
M x2 dx |
ρ |
2 |
dF, |
2 |
2 |
|
||||
F |
2GJρ |
|
2GJρ |
F |
|
|
где интеграл вида ρ2dF есть полярный момент инерции сечения Jρ . Окон-
F
чательно имеем:
Uax M x |
M x2 dx |
|
|
. |
|
2 |
||
|
2GJρ |
|
10
