Sb95841

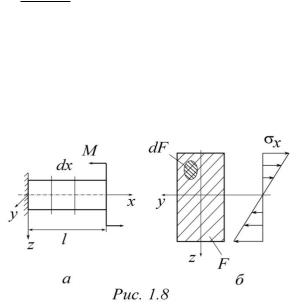
Потенциальная энергия деформации стержня длиною l при кручении имеет вид

l M 2 dx UM x x 2 .

0 2GJρ

На рис. 1.8, а показан стержень, испытывающий деформацию чистого изгиба; на рис. 1.8, б дано распределение нормального составляющего напряжения, возникающего в сечении.

При чистом изгибе нормальные составляющие напряжения

При чистом изгибе нормальные составляющие напряжения ζx меняются по сечению (рис. 1.8, б). Поэтому при вычислении потенциальной энергии элементарного объема выделенного элемента необходимо в сечении выделить элементарную площадку dF и проинтегрировать полученное выражение по площади сечения F :

где z2dF J y – осевой момент инерции сечения относительно оси коорди-

F

нат z. Потенциальная энергия деформации стержня длиной l

11

Аналогично потенциальная энергия для стержня, испытывающего чистый изгиб в плоскости xOy,

Рассмотрим потенциальную энергию стержня, испытывающего деформацию плоско-поперечного изгиба (рис. 1.9, а). На рис. 1.9, б представлено распределение нормальных и касательных составляющих напряжений по сечению стержня.

Потенциальная энергия деформации элементарного объема выделенного элемента вычисляется аналогично потенциальной энергии при чистом изгибе, при этом разделим и умножим полученное выражение на F :

12

Аналогично, когда силы и моменты сил действуют в плоскости xOy,

Окончательно потенциальная энергия деформации стержня при общем пространственном нагружении, когда возникают все шесть внутренних усилий, имеет вид

1.2.4. Теорема Кастильяно

Теорема Кастильяно устанавливает зависимость между обобщенным перемещением и потенциальной энергией. Пусть к твердому телу приложена обобщенная сила Р. От силы Р тело получило перемещение δ . Работа силы Р на перемещение δ , а следовательно, и потенциальная энергия деформации будет равна A U Pδ.

Дадим силе приращение dP. Твердое тело от силы dP получит перемещение dδ и, соответственно, потенциальная энергия получит приращение

U U dP.

P

Приложим силы в обратном порядке. Сначала приложим силу dP, и она на перемещении dδ совершит работу 12 dP dδ . Затем приложим силу Р, и она

совершит работу на перемещение δ, которая будет равна потенциальной энергии U . Одновременно сила dP , приложенная раньше, совершит работу на перемещение δ – dPδ .

Сопоставим потенциальную энергию деформации в первом случае приложения сил и во втором:

13

U U dP U 1 dP dδ dPδ.

P 2

Членом 12 dP dδ можно пренебречь как величиной второго порядка ма-

лости, и тогда имеем

δ U .

ρ

Отсюда следует формулировка теоремы Кастильяно: обобщенное перемещение равно частной производной от потенциальной энергии по обобщенной силе.

В общем случае для стержня, испытывающего деформации растяжениясжатия, кручения и изгиба, теорема Кастильяно имеет вид

Процесс расчета перемещений по данной формуле заключается в составлении уравнений для внутренних усилий по участкам стержня, вычисления производных от них по некоторой обобщенной силе и вычисления интегралов.

Если вычислению подлежат перемещения в сечениях, где не приложена внешняя сила (это относится к деформации изгиба), то прибегают к искусственному приему дополнения нагрузки, т. е. в данном сечении прикладывается фиктивная сила, равная нулю, если определяется линейное перемещение (рис. 1.10, а), или фиктивный момент, равный нулю, если определяется угловое перемещение (рис. 1.10, б).

P 0

ф

A

A

Рис. 4.9 Рис. 1.10

14

Пример 1.2. Рассмотрим конструкцию, расчетная схема которой представлена на рис. 1.11, а. Стержень жестко закреплен в крайнем правом сечении. В левом сечении стержня действует сила Р. Длина стержня l. Жесткость EJ y стержня при изгибе постоянна по длине стержня.

Требуется определить перемещение w0 сечения стержня под действием силы P.

Решение:

1.Проведем оси координат. Начало координат выберем в крайнем левом сечении, направим ось x вдоль оси стержня, ось z – вниз, а ось y – перпендикулярно плоскости чертежа так, чтобы система координатных осей стала правой.

2.Искомое линейное перемещение uz0 считаем обобщенным переме-

щением: uz0 .

3. Обобщенной силой, соответствующей обобщенному перемещению, является сила Р, действующая в сечении, где определяется перемещение:

P P .

об

4. Реакции опоры можно не определять, если рассматривать равновесие отсеченной левой части при составлении уравнения изгибающего момента M y .

15

5. Проведем сечение на расстоянии x от начала координат (рис. 1.11, а) и рассмотрим равновесие левой отсеченной части стержня. Запишем уравнение изгибающего момента M y и производной изгибающего момента по обоб-

щенной силе:

Пример 1.3. Рассмотрим конструкцию, расчетная схема которой приведена на рис. 1.11, б. Стержень жестко закреплен в крайнем левом сечении. Сила Р действует на правом торце стержня. Длина стержня – l. Жесткость стержня при изгибе EJ y const .

Требуется определить перемещение uzA сечения стержня на расстоянии x = l/2 от начала координат.

Решение:

1.Проведем оси координат. Начало координат выберем в крайнем левом сечении, направим ось x вдоль оси стержня, ось z – вниз, а ось y – перпендикулярно плоскости чертежа так, чтобы система координатных осей стала правой.

2.Искомое линейное перемещение uzA считаем обобщенным переме-

щением: uzA .

3. Обобщенная сила, соответствующая обобщенному перемещению, в сечении x = l/2 отсутствует. Для того чтобы можно было воспользоваться теоремой Кастильяно, приложим в этом сечении некоторую дополнительную силу Pд 0. Значение перемещения uzA при этом не изменится. Тогда обоб-

щенная сила, соответствующая обобщенному перемещению: Pоб Pд .

4. Реакции опоры можно не определять, если рассматривать равновесие правой отсеченной части при составлении уравнения изгибающего момента M y в сечениях стержня.

16

5. Точка А разделяет стержень на два участка. Запишем уравнения изгибающего момента на каждом участке и подсчитаем значение производной изгибающего момента по обобщенной силе.

Первый участок: x 0, l2 :

6. По формуле (1.4) определим перемещение uzA с учетом того, что

Pд 0:

Пример 1.4. Рассмотрим конструкцию, расчетная схема которой приведена на рис. 1.11, в. Стержень закреплен двумя опорами. Момент M0 действует посередине пролета стержня. Длина стержня равна l. Жесткость стержня при изгибе EJ y const .

Требуется определить угол поворота C сечения стержня при x l2 . Решение.

1.Проведем оси координат. Начало координат выберем в крайнем левом сечении, направим ось x вдоль оси стержня, ось z – вниз, а ось y – перпендикулярно плоскости чертежа так, чтобы система координатных осей стала правой.

2.Искомое перемещение – угол поворота сечения C – считаем обоб-

щенным перемещением: C .

3. Обобщенная сила, соответствующая обобщенному перемещению, – это сосредоточенный момент M0 в этом сечении вместе с опорными реак-

циями, которые зависят от M0 : Pоб M0 .

4. Реакции опор обозначены на рис. 1.11, в. Определим их, составив уравнения равновесия системы:

17

5. Запишем уравнения изгибающего момента в сечениях стержня на каждом участке и подсчитаем значение производной изгибающего момента по обобщенной силе.

Первый участок x 0, l2 :

Второй участок: x l2, l :

Замечание. Положительное значение угла поворота означает, что поворот сечения произошел в направлении действия обобщенной силы – момента M0 .

1.2.5. Формула Максвелла–Мора

Внутренние усилия, входящие в (1.4), являются линейными функциями приложенных сил Pi и могут быть записаны в форме сумм:

18

Производная от внутреннего усилия по обобщенной силе есть внутреннее усилие от внешней силы, равной единице.

Окончательно формула Максвелла–Мора имеет вид

где N, ..., Qz – внутренние усилия от единичной силы.

При определении перемещений по формуле Максвелла–Мора необходимо в сечении, где вычисляется перемещение, приложить внешнюю силу

того, приложены в этом сечении какие-либо внешние силы или нет. Изложенные энергетические методы механики твердого деформирован-

ного тела широко используются при решении статически неопределимых задач. Известны два метода расчета статически неопределимых систем – метод сил и метод перемещений. В первом за лишние неизвестные принимаются силы, во втором – перемещения.

Пример 1.5. Рассмотрим конструкцию, расчетная схема которой показана на рис. 1.12. Стержень длиной 2а = 1 м закреплен на двух опорах и нагружен равномерно распределенной по длине силой q = 100 Н/м. Жесткость стержня при изгибе постоянна: EJ y const . Материал стержня – сталь СТ5.

Поперечное сечение стержня – прямоугольник шириной b = 2 см и высотой h = 4 см.

19

Требуется определить перемещение середины стержня (точка С). Решение:

1.Проведем оси координат. Начало координат выберем в крайнем левом сечении, направим ось x вдоль оси стержня, ось z – вниз, а ось y – перпендикулярно плоскости чертежа так, чтобы система координатных осей стала правой.

2.Искомое линейное перемещение C определим по формуле (1.6). Уч-

тем, что при изгибе отличен от нуля только изгибающий момент M y , а влия-

нием перерезывающей силы Qz для длинного стержня можно пренебречь:

(рис. 1.12). Вследствие симметрии задачи обе опорные реакции одинаковы: R qa. Стержень имеет один грузовой участок. Изгибающий момент най-

дем, используя метод сечений: M y qax qx2 2.

4. Рассмотрим теперь стержень, нагруженный только единичной силой P = 1 (рис. 1.12). В этом случае реакции опор равны 0.5. Стержень имеет два грузовых участка. Определим методом сечений изгибающий момент от еди-

20