
Sb94863
.pdfМИНОБРНАУКИ РОССИИ
–––––––——————————–––––––
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)
————————————————————
А. В. МОРОЗОВА
ВВЕДЕНИЕ В МАТЕМАТИКУ
Учебно-методическое пособие
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2016
1
УДК 51(07)
ББК В1я7
М 80
Морозова А.В.
М80 Введение в математику: учеб.-метод. пособие для подготовительных курсов для иностранцев СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2016. 32 с.
ISBN 978-5-7629-1925-8
Рассмотрены основные темы и терминология курса математики. Приведены формулы, примеры решения элементарных задач по алгебре и теории множеств. Может быть использовано для организации работы на практических занятиях.
Предназначено для иностранных студентов и преподавателей подготовительного отделения.
Рецензент – канд. физ.-мат. наук С. Б. Колоницкий (СПбГУ).
Утверждено редакционно-издательским советом университета
в качестве учебно-методического пособия
ISBN 978-5-7629-1925-8 |
СПбГЭТУ «ЛЭТИ», 2016 |
2

Математические символы и некоторые понятия математической системы
|
Математические символы |
|
|
Геометрические фигуры |
||||
Символ |
Называют |
Фигура, |
Называют |
|||||
символ |
||||||||
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
для любого |
|
|
|
прямоугольник |
|||
|
|
|
|
|
|
|
|
|
|
существует |
|
квадрат |
|||||
|
|
|
|
|
|
|
|
|
! |
существует единственный |
|
круг |
|||||
|
|
|
|
|
|
|
|
|
или |
|
|
не существует |
|
окружность |
|||
|
||||||||
|
|
|
|
|
|
|||
■ |
конец доказательства |
|
треугольник |
|||||
|
|
|
|
|
|
|||
|
плюс |
, |
следует |
|||||
|
минус |
|
равносильно |
|||||
|
умножить |
|
|
и |
||||
: |
|
|
разделить |
|
|
или |
||
|
|
|
|
|
|
|||
|
равно |
Ø |
|
пустое множество |
||||
|
не равно |
|
плюс бесконечность |
|||||
|
меньше |
|
минус бесконечность |
|||||
|
больше |
, |
фигурные скобки |
|||||
|
меньше или равно |
( , ) |
скобки |
|||||
|
больше или равно |
! |
|
факториал |
||||
|
|
|
|
|
|
|||
|
подмножество (содержит) |
|
|
|
модуль |
|||
|
|
|
||||||
|
|
|
|
|||||
|
пересечение |
lim |
предел |
|||||
|
объединение |
const |
постоянная величина |
|||||
|
принадлежит |
|
|
сумма |
||||
|
не принадлежит |
|
|
произведение |
||||
Определение: теорема – это утверждение, истинность которого выведена только на основе определений, свойств и ранее полученных утверждений с помощью логических правил.
Определение: доказательство теоремы – это вывод, с помощью кото-
рого получена истинность утверждения.
3
ВВЕДЕНИЕ
Методические указания предназначены иностранным слушателям центра довузовской подготовки СПбГТЭУ «ЛЭТИ» на начальном этапе изучения русского языка.
Основной целью данного издания является подготовка слушателей к восприятию математики и других технических дисциплин на русском языке.
Изложение материала начинается с самых элементарных математических понятий в их максимально упрощенном варианте. Определения и строгие теоретические построения часто сопровождаются пояснениями и примерами. Это позволяет учесть некоторое несовпадение исходного уровня знаний математики у слушателей, прибывших из разных стран. Тем, кто имеет достаточную математическую подготовку, указания будут полезными для освоения математической лексики.
Слушателям рекомендуется для лучшего усвоения материала и повышения эффективности самостоятельной работы составлять для себя словарьсправочник терминов, используемых при изучении математики на неродном языке. Эти слова и словосочетания в тексте выделены жирным шрифтом. Рекомендуется также выполнять задания, приведённые в данных методических указаниях и отвечать на вопросы, сформулированные в конце каждой главы.
ГЛАВА I. ЧИСЛОВЫЕ МНОЖЕСТВА
ИОСНОВНЫЕ АРИФМЕТИЧЕСКИЕ ОПЕРАЦИИ
1.МНОЖЕСТВА И ДЕЙСТВИЯ НАД НИМИ
1.1.Понятие множества
ВXIX в. немецкий математик Георг Кантор (1845–1919) создал новую область математики – теорию бесконечных множеств. Через несколько десятилетий почти вся математика была перестроена на теоретико-множествен- ной основе. Понятие множества в математике является первичным, не определяемым, таким же, как понятие точки и прямой в геометрии, и к более простым понятиям не сводится.
Множество – это совокупность объектов, которые объединяют по определённому признаку (множество студентов группы, множество букв алфавита, множество натуральных чисел и т. д.).
Элементы множества – это объекты, из которых состоит множество.
4

Множества обозначают заглавными латинскими буквами A, B, C, ..., элементы обозначают строчными буквами a,b,c, ....
Читают: «множество A состоит из элементов a,b,c ». Пишут:
A a,b,c .
Читают: «элемент a принадлежит множеству A ». Пишут: a A. Читают: «элемент x не принадлежит множеству A ». Пишут: x A. Конечное множество – множество, которое состоит из конечного числа
элементов. Бесконечное множество – множество, которое не является конечным. Пустое множество – это множество, которое не содержит элементов. Пишут O .
Множество можно задать, если перечислить все его элементы. Пример: A a , B 1,2 . Множества A и B – это конечные мно-
жества.
Множество можно задать, если указать свойство его элементов – харак-
теристическое свойство.
Читают: «множество C состоит из элементов x таких, что x больше единицы». Множество C – это бесконечное множество, так как состоит из
бесконечного числа элементов. Пишут: C x x 1 .
Читают: «множество A состоит из элементов a,b,c и так далее».
Пишут: + a,b,c,... .
Определение: множество А называют подмножеством множества В, если каждый элемент множества А принадлежит множеству В.
Читают: «множество А содержится в множестве В или А подмножество В». Пишут: A B .
Пример: множества 1 , 2 , 1,2 , O – это подмножества множества A 1,2 . Пустое множество является подмножеством любого множества.
Определение: множества равны, если они состоят из одних и тех же элементов.
Читают: «множество А равно множествуB ». Пишут: A B . Пример: множества А 1,2,3 и B 2,3,1 равны.
Из определений подмножества и равенства множеств следует, что, если A B , то A B и B A . Если A B и B A , то A B . Это эквивалентно записи: A B A B B A .
5
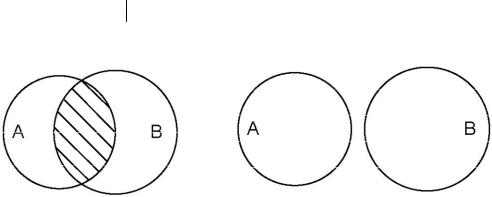
Диаграммы Эйлера–Венна – это удобный инструмент, который позволяет изображать множества и иллюстрировать операции над ними. Множества в диаграммах Эйлера–Венна изображаются внутренними частями кругов, их пересечениями, объединениями и т. д.
1.2. Действия над множествами
Пусть даны два множества A и B . Над ними можно выполнять следующие действия (операции): пересечение множеств, объединение множеств, вычитание множеств.
I. Пересечение множеств (произведение)
Определение: пересечение множества A и множества B – это множество, которое состоит только из общих элементов множества A и множества B .
Читают: «Пересечение множества A и множества B состоит из элементов x таких, что x принадлежит множеству A и x принадлежит множеству
B ». Пишут: A B x x A x B .
Слева на рис.1.1 множество A B заштриховано, а справа A B O .
|
|
|
|
А |
|
В |
А |
В |
|||||
|
|
|
|
|
|
|
Рис.1.1
Примеры:
1.Если A 1,2,3,4,5 , B 1,3,5,7,9 , то A B 1,3,5 .
2.Если C a,b,c , D m,n , то C D O .
Свойства пересечения множеств:
1.A B B A (свойство коммутативности);
2.A O O;
3.A A A ;
4.Если A B , то A B B A .
Аналогично можно определить пересечение трёх, четырёх и любого ко-
нечного и бесконечного числа множеств. Пересечение трёх множеств A, B,C обозначают A B C .
6
Определение: пересечение конечного числа множеств Ai обозначают
k |
|
A1 |
|
A2 |
|
A3 |
|
|
|
Ak |
|
x |
|
x |
|
Ai длявсех i |
|
I, где I |
|
|
|
|
|
||||||||||
|
|
|
|||||||||||||||||||||||||||||||
Ai |
|
|
|
|
|
|
|
|
|
|
|
1,k |
. |
||||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Множество I называют индексным множеством, а i |
– индекс. |
|
|
||||||||||||||||||||||||||||||
Определение: пересечение бесконечного числа множеств Ai |
обозначают |
||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
x |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Ai |
|
A1 |
|
A2 |
|
A3 |
|
|
|
x |
|
Ai |
длявсех i |
|
I, где I |
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
1, . |
|
||||||||||||||||||||||
i 1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
II. Объединение множеств (сумма) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
Определение: объединение множества A и множества B – это множе-
ство, которое состоит из тех и только тех элементов, которые входят хотя бы
в одно из множеств A или B . |
|
|
|
|
|
|
||||||||||||
|
Читают: «объединение множества А и множества B состоит из элемен- |
|||||||||||||||||
тов x |
таких, |
что x |
принадлежит множеству А или x |
принадлежит множе- |
||||||||||||||
ству B ». Пишут: A B |
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
x |
x A или x B . |
|
|||||||||||||||
|
Определение: объединение k множеств Ai обозначают |
|||||||||||||||||
k |
A A A A ... A |
|
|
|
x |
|
x A хотябы дляодного i I, где I {1,2,3,...,k} . |
|||||||||||
|
|
|||||||||||||||||
|
i |
1 |
2 |
|
3 |
k |
|
|
|
|
|
|
i |
|
||||
i 1 |
Определение: объединение бесконечного числа множеств Аi обозначают |
|||||||||||||||||
|
||||||||||||||||||
|
A A A |
|
A |
... |
|
x |
|
x A |
i |
хотя бы для одного i I, где I {1,2,3,...} . |
||||||||
|
|
|||||||||||||||||
|
i |
1 |
2 |
3 |
|
|
|
|
|
|
|
|
|
|
||||
i 1 |
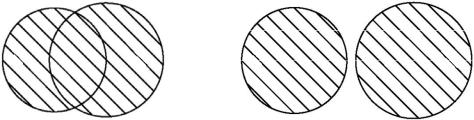
На рис.1.2 множество A B заштриховано. |
|
||||||||||||||||
|
|
|||||||||||||||||
А |
В |
А |
В |
Рис. 1.2
Примеры:
1. Если A 1,3,5 и B 2,4,6 , то A B 1,2,3,4,5,6 .
7

2. Если C a,b,c и D m,n , то C D a,b,c,m,n .
Свойства объединения множеств:
1.A B B A (коммутативное свойство);
2.A O A ;
3.A A A ;
4.Если A B , то A B B .
III. Разность множеств (вычитание)
Определение: разность множества A и множества B – это множество,
которое состоит из всех тех элементов множества A , которые не принадлежат множеству B .
|
|
|
|
Читают: «Разность множества A и множества B |
|||||
|
|
|
|
состоит из элементов x таких, что |
x принадлежит |
||||
А |
|
В |
|
множеству A |
и x не принадлежит множеству B ». |
||||
|
|
|
|
||||||
|
|
|
|
Пишут: A \ B |
|
|
|
|
|
|
|
|
|
|
x |
x A и x |
B . |
|
|
|
Рис. 1.3 |
На рис. 1.3 множество A \ B заштриховано. |
|||||||
|
Примеры: |
|
|
|
|
|
|
||
|
1. Если A 1,2,3,4 и B 1,2 , то A \ B 3,4 . |
|
|||||||
|
2. Если A 1,2 и B 1,2,3 , то A \ B O . |
|
|
||||||
|
Определение: |
симметрическая разность множества |
A и множества |
||||||
B – это множество A \ B B \ A . Пишут A B .
IV. Дополнение множества
Определение: универсальное множество U – множество, у которого все рассматриваемые множества являются его подмножествами. При использовании диаграмм Венна универсальное множество U представляют в виде прямоугольника.
Определение: дополнение множества A – это множество элементов универсального множества U ,
|
|
|
|
|
|
|
которые не принадлежат A . Читают: «А штрих». |
|||
|
|
|
|
|
|
U |
||||
А |
|
|
|
|
|
|||||
|
|
|
|
|
Пишут: |
|
= U\A = {x | x U и x A}. |
|||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
A |
|||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
На рис.1.4 множество A заштриховано. |
|||
|
|
Рис. 1.4 |
|
Пример: если U = {1; 2; 3; 4; 5; 6; 7}, А = {2; 3; 4}, то |
||||||
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
A = {1; 5; 6; 7}. |
|
||
Свойства дополнения множества: |
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
1. |
A |
A ; |
|
2. A A |
U ; |
3. A A O |
||||
|
|
|
||||||||
8
Теорема 1.1. Для произвольных множеств А и В справедливо равенство
|
А\В = А В'. |
Доказательство. Пусть, а А\В. По определению разности множеств |
|
получим (а А) (а В) |
(а А) (а В') а (А В').■ |
Теорема 1.2. Для произвольных множеств А и В справедливы равенства: |
|
1. (А В)' = Ā В'; |
2. (А В)' = Ā В'. |
Доказательство. |
|
1.Пусть а (А В)', тогда по определению дополнения множества получим
а(А В) (а А) (а В) (а Ā) (а В') а ( Ā В').
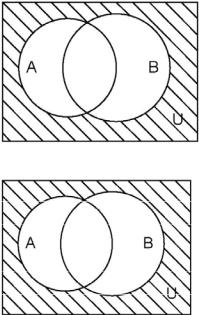
2.Покажем, с помощью диаграмм Эйлера–
Венна, что утверждение 2 теоремы |
(А В)' = |
|
|
|
|
|
|
|
|
|
= Ā В' истинно. Множество (А В)' |
– дополне- |
|
|
|
|
|
|
|
|
|
А |
В |
|||||||||
ние множества (А В), представлено диаграммой |
|
|
|
|
|
|
|
|
|
|
Венна на рис. 1.5, заштрихованной частью. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
U |
|||
Множество Ā В' – пересечение дополне- |
|
Рис. 1.5 |
||||||||
ний множеств А и В. Представлено диаграммой |
|
|||||||||
|
|
|
|
|
|
|
|
|
||
Венна на рис. 1.6 заштрихованной частью. |
|
|
|
|
|
|
|
|
|
|
Получили, что и (А В)', и Ā В' одинаково |
|
|
|
|
|
|
|
|
|
|
изображенынадиаграмме Венна, поэтому (А В)' = |
|
|
|
|
||||||
А |
В |
|||||||||
= Ā В'. ■ |
|
|
|
|
|
|
|
|
|
|
Теорема 1.3. Для произвольных множеств А, |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
U |
||||
В и С справедливы равенства: |
|
|
|
|
|
|
|
|
|
|
1. А (В С) = (А В) (А С); |
Рис. 1.6 |
|
А (В С) = (А В) (А С) (свойства дистрибутивности). 2. А (В С) = (А В) С;
А (В С) = (А В) С (свойства ассоциативности).
Доказательство. 1. Пусть а (А (В С)), тогда по определению пресечения множеств получим (а А) (а (В С)) (а А) ((а В) а С) ((а А) (а В)) ((а А) (а С)) (а (А В)) (а (А С)) а ((А В) (А С)).
2. Доказать самостоятельно. ■ Свойства множеств, сформулированные в приведенных теоремах, могут
быть проверены методом формальных доказательств или на диаграммах Венна–Эйлера.
Переведите на родной язык и выучите слова:
множество; пересечение;
9
элементы множества; |
объединение; |
подмножество; |
индекс; |
принадлежит; |
индексное множество; |
не принадлежит; |
дополнение; |
конечное множество (число); |
разность |
бесконечное множество (число); |
симметрическая разность; |
пустое множество; |
универсальное множество; |
характеристическое свойство; |
истинно; |
свойство коммутативности; |
ложно; |
свойства дистрибутивности; |
диаграммы Венна–Эйлера; |
свойства ассоциативности; |
доказательство; |
разность множеств; |
теорема; |
множества равны; |
свойства. |
2. МНОЖЕСТВО НАТУРАЛЬНЫХ И ЦЕЛЫХ ЧИСЕЛ
2.1. Арифметические операции (действия)
Рассмотрим четыре арифметических действия: сложение, вычитание, умножение и деление (табл. 1).
|
|
|
|
Таблица 1 |
|
Основные арифметические операции |
|
||
|
|
|
|
|
Операция |
Знак |
Пишут |
Читают |
Компоненты |
Сложение |
+ (плюс) |
a b c |
a плюс b равно с |
a, b – слагаемые; |
|
|
|
|
с– сумма |
Вычитание |
– (минус) |
a b c |
a минус b равно с |
a – уменьшаемое; |
|
|
|
|
b – вычитаемое; |
|
|
|
|
с– разность |
Умножение |
· (умножить) |
a b c |
a умножить на b |
a , b – множители; |
|
|
|
равно с |
с– произведение |
Деление |
: (разделить) |
a : b c |
a разделить на b |
a – делимое; |
|
|
|
равно с |
b – делитель; |
|
|
|
|
с– частное |
Свойства действий:
1. |
a b b a, a b b a – коммутативность сложения и умножения; |
2. |
a b c a b c , a b c a b c – ассоциативность сложения |
иумножения;
3.a b c a c b c, a b : c a : c b : c.
10
