
Sb94863
.pdf
Решение. Пусть А – 100 %, x – p % . Тогда x = A100p . 3. Сколько процентов число B составляет от числа A?
Решение. А – 100 %, B – x % . Тогда x = B 100 .
A
7. СТЕПЕНЬ ДЕЙСТВИТЕЛЬНОГО ЧИСЛА
7.1. Степень с целым показателем
Определение: степенью ненулевого числа а с натуральным показателем n, большим или равным 1, называют произведение n множителей, каждый из которых равен а:
|
an a a a (n раз), a ≠ 0, n N. |
|||
Операция |
Пишут |
Читают |
Компоненты |
|
|
|
|
|
|
возведение |
|
|
а – основание; |
|
аn = b |
а в степени n равно b |
n – показательстепени; |
||
в степень |
||||
|
|
b – степень |
||
|
|
|
||
Читаем: a2 – «a в степени два или a в квадрате»; a3 – «a в степени три или a в кубе»;
a4 – «a в степени четыре или a в четвёртой степени»; an – «a в степени n или a в энной степени».
Определение: a n a1n , n N, a 0.
Каждое рациональное число, большее 10 можно записать в виде а·10n, где 1 ≤ а < 10 и n N. Эту запись называют стандартным видом числа.
Пример: 4578 = 4,578·103; 45,78 = 4,578·10; 107008 = 1,07008·105.
7.2. Степень с рациональным показателем
m |
|
m |
Определение: a n n am , а > 0, |
m Z, |
n N. 0 n = 0. |
Читаем: а в степени mn равно корень степени n из a в степени m.
Операция |
Знак |
Пишут |
Читают |
Компоненты |
|
|
|
|
|
|
|
Извлечение |
|
n a b |
корень |
степени |
a – подкоренное |
корня |
радикал |
|
n из a |
равен b |
число; |
|
|
|
|
|
|
21
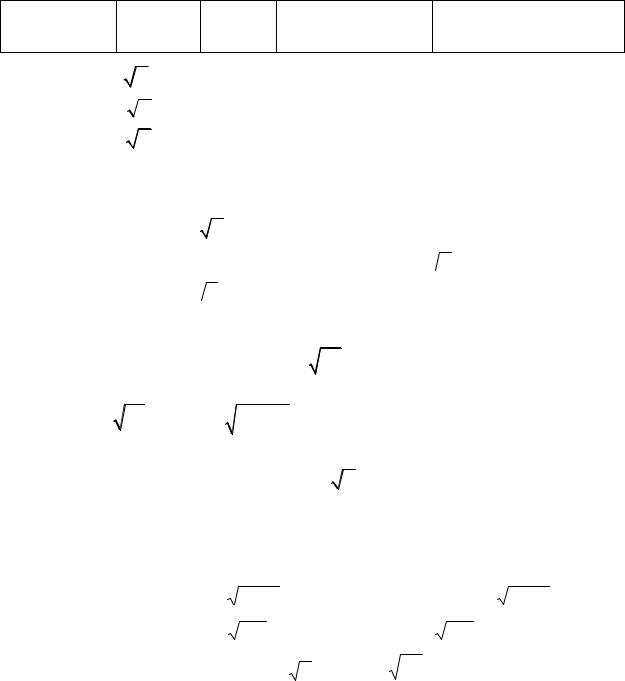
n – показатель корня; b– корень
Читаем: 3 a – «корень кубический из a»;
4 a – «корень четвёртой степени из a»;
n a – «корень энной степени (степени n) из a». Определение: неотрицательное число, квадрат которого равен неотрица-
тельному числу а, называют квадратным корнем. a b b2 a, a 0, b 0
Читают: «квадратный корень числа a ». Пишут:  a .
a .
По определению: (  a )2 = a при a ≥ 0. Из отрицательных чисел нельзя извлекать квадратные корни, так как квадрат любого числа неотрицателен.
a )2 = a при a ≥ 0. Из отрицательных чисел нельзя извлекать квадратные корни, так как квадрат любого числа неотрицателен.
a R верно равенство a2 |
|
|
|
a |
|
a, еслиa 0; |
|||||||
|
|
|
|
||||||||||
Пример: 82 |
|
|
|
|
( 12)2 |
|
|
|
|
|
|
|
a, еслиa 0. |
|
|
|
|
|
|
|
|
|
|
||||
|
8 |
|
8; |
|
12 |
|
12 . |
||||||
|
|
|
|
||||||||||
Определение: арифметический корень степени n из числа a ( a ≥ 0) –
это такое число b (b ≥ 0), что bn = a : n a b bn = a , где a ≥ 0, b ≥ 0, n N (n ≠ 1).
Определение: корнем нечетной степени n из действительного числа a называют такое число b, что bn a , где a R .
Примеры.1. Вычислим 3 125; b3 125; ( 5)3 125 и 3 125 5. 2. Вычислим 3 125; b3 125; 53 125 и 3 125 5.
Если n нечетно, то равенства (n a)n a и n an a верны и для отрицательных значений a .
Основные свойства степени:
1.an am an m, n,m Q ;
2.an : am an m , a ≠ 0;
3.an m an m ;
4.a b n an bn ;
22
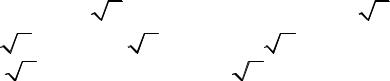
5. |
a n |
|
an |
, b ≠ 0; |
|
|
|
bn |
|||
|
b |
|
|
||
6.a0 = 1, a ≠ 0, значение 00 – неопределенно;
7.Если a и b – положительные числа и для некоторого действительного
числа n ≠ 0 выполняется равенство an 8. Если a – положительное число
bn, то a = b.
идля некоторых действительных чисел
n, m ≠ 0 выполняется равенство an am , то n = m.
Примеры:
1. |
Вычислить: |
|
332 3 914 |
|
332 3 328 |
329(33 1) |
|
26 |
|
|
1. |
|
|||||||||||||||||||
|
26 2710 |
|
|
26 330 |
26 |
3 |
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
26 330 |
|
|
3 |
|
||||||||||||||||
2. |
Упростите: |
92n 3 32n 2 |
|
34n 6 |
32n 2 |
36n 4 |
34 |
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
81 |
|
|
||||||||||
|
|
27 |
|
2n |
|
|
|
|
|
6n |
|
6n |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
3 |
|
|
3 |
|
|
|
|
|
|
|
|
|
|||||||
3. |
Вычислить: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
3 |
0 ,3 : |
|
3 0 , 2 |
|
|
|
|
|
|
2 |
|
|
|
|
3 0 ,3 (1 3 0 ,5 ) |
|
|
|
|
2 |
|
|
|||||||||
|
|
1 |
3 0 ,5 |
|
|
1 |
|
|
3 |
|
|
|
3 0 , 2 |
|
|
1 |
|
3 |
|
||||||||||||
|
3 0 ,5 |
(1 3 ) 2 |
|
|
2 |
|
|
|
3 2 3 3 |
3 2 |
|
4 |
|
||||||||||||||||||
|
|
1 |
|
|
3 |
|
|
|
|
|
|
|
|
|
1 |
3 |
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
Переведите на родной язык и выучите слова:
отношение; пропорция; члены пропорции;
крайние члены пропорции; средние члены пропорции; основное свойство пропорции;
Вопросы для повторения:
степень; стандартный вид числа; квадратный корень; показатель степени; арифметический корень;
неизвестный член пропорции.
1.Что такое множество?
2.При каких условиях два множества равны?
3.Что такое пересечение и объединение множеств?
4.Что такое разность и дополнение множеств?
5.Как записывают любое четное и нечетное число?
6.Какие числа называют простыми и составными?
7.Что такое правильная и неправильная дробь?
23

8.Назовите основное свойство дроби.
9.Какое число называют рациональным и иррациональным?
10.Какие числовые множества и числовые интервалы вы знаете?
11.Что такое модуль действительного числа?
12.Что называют пропорцией?
13.Назовите основное свойство пропорции.
14.Перечислите арифметические операции.
ГЛАВА II. ПРЕОБРАЗОВАНИЕ АЛГЕБРАИЧЕСКИХ ВЫРАЖЕНИЙ
1. ЦЕЛЫЕ РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
Выражение вида 2x y 7x называют выражением с переменными,
где x и y – это переменные (переменные – величины, которые принимают различные числовые значения). Числа, которые стоят перед переменными: 2, 1, –7 – это коэффициенты.
Целое рациональное выражение – это выражение, которое не содер-
жит деления на выражения с переменными. Рассмотрим целые рациональные выражения.
1.1. Одночлен и многочлен
Одночлен – это выражение, которое содержит только действия умножения и возведения в степень над числами и переменными.
Пример: 3x2 ; 8,5a2b; 1 |
4 |
x y z ; |
x3 2 y – это одночлены. |
|
|
|
|
Степень одночлена – это сумма показателей степеней всех букв, кото- |
|||
рые входят в этот одночлен. |
|
|
|
Пример: степень одночлена 8a3b равна 4; степень одночлена xy равна 2.
Стандартный вид одночлена – это одночлен, у которого числовой множитель (коэффициент) стоит на первом месте, произведение одинаковых переменных записано в виде степени.
Пример: одночлен x2 2y x3 в стандартном виде будет иметь вид 2x5 y .
Подобные одночлены – это одночлены, которые в стандартном виде отличаются только коэффициентами.
Пример: 2x2y и –3x2y; 12 x3 и 2x2·x – это подобные одночлены.
24

Привести подобные члены (одночлены) значит сложить коэффициенты подобных одночленов и результат умножить на общее буквенное выражение.
Пример: привести подобные члены: 3a2b – 5a2b + a2b.
Решение. 3a2b – 5a2b + a2b = (3 – 5 + 1)a2b = –a2b. Ответ: –a2b.
Многочлен – это алгебраическая сумма одночленов.
Пример: 2x2 + 3x, a + b + c; 11 – 4x2y2 + xy – это многочлены.
Старший член многочлена – это член многочлена с самой большой степенью. Степень многочлена – это степень его старшего члена.
Пример: степень многочлена 8x3 + 2xy – 9x равна 3, степень многочлена 1 + x2 + x5 равна 5.
Коэффициент при старшем члене многочлена – это число, на которое умножен старший член многочлена.
Стандартный вид многочлена – это многочлен, члены которого записаны в стандартном виде, в порядке уменьшения степеней и приведены подобные члены.
Пример: многочлен 3a·5b + 3ab + 2a(–b) + b в стандартном виде будет записан в виде: 15ab + 3ab – 2ab + b = 16ab + b.
На множестве многочленов выполняются операции сложения, вычитания, умножения и деления многочленов.
Пример: вычислить
48b2 (5a 3b) 6b |
|
48b2 |
30ab 18b2 |
b a |
|
b a |
|
|
|
Деление многочлена на многочлен:
(xy – 7x + 2y – 14) : (x + 2) = y – 7 xy 7x 2y 14 x 2
xy 2y y 7
7x 147x 14 0
|
30b2 30ab |
|
|
|
30b(b a) |
|
30b . |
||
b a |
|
|
b a |
||||||
|
|
|
|
|
|
||||
|
( x2 |
2x 3):(x+2) = x+ |
3 |
|
|||||
|
x 2 |
||||||||
|
|
|
|
|
|
|
|
||
|
x2 |
2x 3 |
|
x 2 |
|
|
|||
|
|
|
|
||||||
|
x2 |
2x |
|
|
x |
|
|
|
|
|
|
3 |
|
|
|
|
|
|
|
1.2. Формулы сокращённого умножения
При умножении многочлена на многочлен используют формулы со-
кращённого умножения.
1. (a + b)·(a – b) = a2 – ab + ab – b2 = a2 – b2.
25
a2 b2 (a b)(a b) – разность квадратов. Разность квадратов двух
чисел равна произведению суммы этих чисел на их разность.
2. (a + b)2 = (a + b)·( a + b) = a2+ab + ab + b2 = a2 + 2ab + b2.
(a b)2 a2 2ab b2 – квадрат суммы. Квадрат суммы двух чисел
равен сумме квадратов этих чисел плюс их удвоенное произведение. 3. (a – b)2 = (a – b)·(a – b) = a2 – ab – ab + b2.
(a b)2 a2 2ab b2 – квадрат разности. Квадрат разности двух чисел равен сумме квадратов этих чисел минус их удвоенное произведение.
4. (a + b)·(a2 – ab + b2) = a3 – a2b + ab2 + a2b – ab2 + b3 = a3 + b3.
a3 b3 (a b)(a2 ab b2 ) – сумма кубов. Сумма кубов двух чисел равна произведению суммы этих чисел на неполный квадрат их разности.
5. (a – b)·(a2 + ab + b2) = a3 + a2b + ab2 – a2b – ab2 – b3 = a3 – b3.
a3 b3 (a b)(a2 ab b2 ) – разность кубов. Разность кубов двух чиселравнапроизведениюразностиэтихчиселнанеполныйквадратихсуммы.
6.(a + b)3 = (a + b)2(a + b) = (a2 + 2ab + b2)(a + b) = a3 + a2b + 2a2b +
+2ab2 + ab2 + b3 = a3 + 3a2b + 3ab2 + b3.
(a b)3 a3 b3 3ab(a b) – куб суммы. Куб суммы двух чисел равен сумме кубов этих чисел плюс их утроенное произведение на их сумму.
7. (a – b)3 = (a – b)2(a – b)=(a2 – 2ab + b2)(a – b) = a3 – a2b – 2a2b + 2ab2 + + ab2 – b3 = a3 – 3a2b + 3ab2 – b3.
(a b)3 a3 b3 3ab(a b) – куб разности. Куб разности двух чисел равен разности кубов этих чисел минус их утроенное произведение на их разность.
Пример: выполнить действия с помощью формул сокращённого умножения:
1. (3xy + 1)(3xy – 1);
3. (1 + m2)(1 – m2 + m4); 5) (2a – 3b)3.
Решение:
1.По формуле 1 получим: (3xy + 1)(3xy – 1) = (3xy)2 – 12 = 9x2y2 – 1.
2.По формуле 2 получим: (x2 + y2) = (x2)2 + 2x2y2 + (y2)2 = x4 + 2x2y2 + y4.
3.По формуле 4 получим: (1 + m2)(1 – m2 + m4) = 13+(m2)3 = 1 + m6.
26
4.По формуле 5 получим: (3a – 4)(9a2 + 12a + 16) = (3a)3– 43 = 27a3 – 64.
5.По формуле 7 получим: (2a–3b)3 = (2a)3 – 3(2a)2 · 3b + 3·2a(3b)2 –
–(3b)3 = 8a3 – 36a2b + 54ab2 – 27b3.
1.3.Разложение многочлена на множители
1.Вынесение общего множителя за скобки:
а) 15x2 5xy 5x(3x y) ; б) 49b2 7ab 7b(7b a) . 2. Способ группировки:
а) x4 5x2 9 (x4 6x2 9) x2 (x2 3)2 x2 (x2 3 x)(x2 3 x) ; б) x4 3x2 4 (x4 4x2 4) x2 (x2 2)2 x2 (x2 2 x)(x2 2 x) . 3. Использование формул сокращенного умножения.
а) a2 14ab 49b2 (a 7b)2 ; б) 9x2 6xy y2 (3x y)2 .
1.4. Формула бинома Ньютона
Для произвольной степени n N справедлива формула бинома Ньютона:
|
|
|
n |
|
|
|
|
(a + b)n = Cnk · an–k · bk, |
|
|
|
|
k 0 |
|
где Cnk |
n! |
|
– число сочетаний из n по k, n! = 1·2·3…·n – n факториал. |
|
k!(n k)! |
||||
|
|
|||
Полагают 0! = 1. Cnk называют биномиальными коэффициентами.
Переведите на родной язык и выучите слова:
переменная; |
многочлен; |
выражение с переменной; |
степень многочлена; |
коэффициент; |
коэффициент при старшем члене; |
одночлен; |
формулы сокращённого умножения; |
степень одночлена; |
формула Бином Ньютона; |
привести подобные члены; |
число сочетаний из n по k. |
27
2.ДРОБНО-РАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
ИИРРАЦИОНАЛЬНЫЕ ВЫРАЖЕНИЯ
2.1. Основные понятия
Дробно-рациональное выражение – это выражение, которое содержит деление на выражение с переменными.
|
|
2y y2 |
|
|
|
|
|
1 |
|
1 |
|
|
||
Пример: |
1 |
a b c |
|
1 |
|
x |
y |
|
|
|||||
|
|
y2 |
, |
|
a |
c |
, |
|
|
|
|
– дробно-рациональные |
||
|
|
|
|
2 |
|
|
||||||||
|
|
|
4 |
|
|
|
|
|
|
|
||||
выражения. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Выражение |
|
x2 |
y2 |
3z2 |
|
|
|
|
|
|
|
|
||
|
|
|
|
не дробное, так как не содержит деление на |
||||||||||
|
|
3 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
выражение с переменной |
и может |
|
быть |
записано в виде многочлена: |
||||||||||
13 x2 13 y2 z2.
Выражение вида BA называют дробью, если A и B – числовые выражения или выражения с переменными.
Арифметические дроби: |
2 |
; |
(12 3) 5; |
|
|
|
15 |
|
. |
|
|||
3 |
18 |
3 8 |
|
||||||||||
|
|
0,2 |
|
|
|
||||||||
Алгебраические дроби: |
5 |
; |
|
x2 x |
; |
a b |
; |
10x2 y |
. |
||||
x |
|
x 1 |
a2 |
|
|
x y |
|
||||||
|
|
|
|
|
|
|
|
|
|||||
Алгебраическая дробь BA имеет смысл (существует, определена), если
B ≠ 0.
Определение: область определения (D) алгебраической дроби с одной
переменной – это множество значений переменной, при которых дробь BA
имеет смысл.
Пример: дробь x имеет смысл при всех значениях переменной x, x2 1
кроме тех x, которые равны 1, то есть x 1. Поэтому
D = R\{–1;1} или D = (– ; –1) (–1; 1) (1; + ).
28
Если дана алгебраическая дробь с двумя переменными x и y, то область определения этой дроби есть множество пар (x; y), при которых дробь имеет смысл.
Пример: дробь |
10x2 y |
имеет смысл, если x ≠ y. Поэтому D = {(x; y) | x R, |
||
x |
y |
|||
|
|
|||
y R, x ≠ y}.
2.2. Действия с алгебраическими дробями
Сложение и вычитание алгебраических дробей:
A B AD BC ; C 0, D 0 . C D CD
Умножение алгебраических дробей:
CA DB CA DB ; C 0, D 0.
Деление алгебраических дробей:
CA : DB CA DB ; C 0, D 0, B 0 .
Пример:
1) |
|
a2 9 |
|
|
1 |
|
|
2 |
|
|
|
a(a 3) (a2 9) |
|
a 3 6 |
|
|
|||||||||
a |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
a 3 |
3 |
a |
|
|
|
|
|
a 3 |
3(a |
3) |
|
|
|||||||||||||
|
|
|
|
|
3 |
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(3a 9) (a 3) |
|
3(a 3) |
1 |
|
|
|
|
|
|
|
|
|
|
|||||||||||
3(a 3)(a 3) |
3(a 3) |
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
2) |
|
9 4b2 |
|
1 |
|
|
|
2 |
|
|
|
3(3 2b) (9 4b2) |
|
2b(3 2b) |
|
||||||||||
3 |
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
3 2b |
|
|
|
3 |
|
|
|
|
3 2b |
|
|
(3 |
2b) 4b |
||||||||||||
|
|
|
|
2b |
|
2b |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(6b 4b2)2b(3 2b) |
4b2(3 2b) |
4b2 |
|
|
|
|
|
|
|
|||||||||||||||
|
(3 2b) (3 2b) |
|
|
|
|
(3 2b) |
|
|
|
|
|
|
|
|
|||||||||||
Основное свойство дроби: величина дроби не изменится, если её числитель и знаменатель умножить (разделить) на одно и то же число (выражение), не равное нулю:
A |
|
A C |
|
A D |
, где B ≠ 0, C ≠ 0, D ≠ 0. |
||
B |
|
B C |
B D |
||||
|
|
|
|||||
Алгебраические дроби можно сократить (см. гл. I, п. 3.1).
29
2.3. Иррациональные выражения
Иррациональное выражение – это выражение, которое содержит корни и степени с дробным рациональным показателем.
Примеры: 3 x; |
a |
b; |
2 |
; x |
1 |
2 y |
1 |
2 – это иррациональные |
x y |
|
|
||||||
|
|
|
|
|
|
|
|
выражения.
Определение: область определения иррационального выражения (D)
с одной переменной – это множество значений переменной, при которых выражение имеет смысл.
Пример:
1. Выражение  x 1 имеет смысл, если (x – 1) ≥ 0. Значит
x 1 имеет смысл, если (x – 1) ≥ 0. Значит
D= {x | x R, x – 1 ≥ 0} = {x | x R, x ≥ 1} = [1;+∞).
2.Выражение  x
x  x 2 имеет смысл, если (x – 2) ≥ 0 и x ≥ 0. Значит
x 2 имеет смысл, если (x – 2) ≥ 0 и x ≥ 0. Значит
D = D1 D2 = {x | x R, x – 2 ≥ 0} {x | x R, x ≥ 0} = [2;+∞).
Преобразования иррациональных выражений. Преобразования ирра-
циональных выражений выполняют на основе свойств арифметического корня, степени с дробным рациональным показателем, а также с использованием формул сокращенного умножения и свойств алгебраической дроби.
Примеры:
1. Упростите выражение:
( 11x
11x  7) (
7) ( 7
7  11x) (
11x) ( 18
18  2)2 11x 7 (18 2
2)2 11x 7 (18 2  36 2) 11x 39. 2. Упростите выражение:
36 2) 11x 39. 2. Упростите выражение:
|
|
|
|
a b |
|
|
|
a b |
|
|
b |
|
|
|
|
|
|
a |
|
|
|
( |
a b)2 |
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
b |
a |
|
b |
ab |
|
ab |
|
|
|
|
|
2 |
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
a b |
|
|
|
a |
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
a b |
|
: |
|
ab(a b) b a( |
|
|
|
a b) a b( |
a b) |
|
|
a b |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||||||||
b |
|
a |
|
|
|
|
|
|
|
|
|
ab(a b) |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
a b |
|
|
: |
2 ab(a b) |
|
a b |
|
|
|
a b |
|
|
|
|
a b |
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||||||
|
|
b a |
|
|
|
2 |
|
|
|
2 |
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
ab(a b) |
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
0, |
если a b 0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
a |
b, если0 a b |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
30
