
Sb98341
.pdf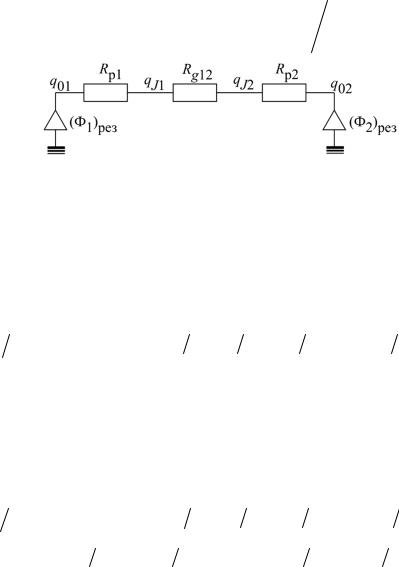
1 рез (12) 1 рез; |
1 рез q01 q02 |
|
1 |
|
1 |
|
2 |
|
|
|
|
|
|||||
|
1A1 |
A1F12 |
|
|
||||
|
|
|
|
|
2A2 . |
|||
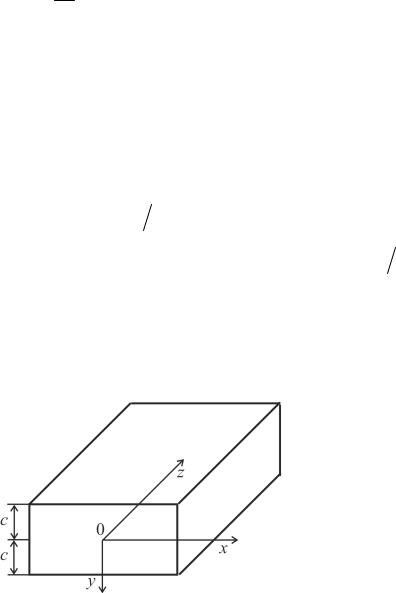
Рис. 4.1
Здесь обозначения прежние. Индексом 1 обозначены характеристики нагревателя, а индексом 2 – загрузки.
Если загрузка занимает большую часть пространства печи ( A1 A2 ), то F12 = 1 и плотность результирующего теплового потока и потока теплообмена между нагревателем и изделием будет равна
(12) |
A1 q(12) q01 q02 A1 1 |
A1 1 1 A2F21 2 |
A2 2 |
|
q01 q02  1
1 1 1 2
1 1 2  2 c12 T1 273 4 T2 273 4 ,
2 c12 T1 273 4 T2 273 4 ,
где c12  1 1
1 1 1 2
1 2 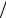 2 – приведенная излучательная способность системы.
2 – приведенная излучательная способность системы.
Если нагреваемое изделие маленькое, т. е. A2 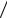 A1 0 , то в этом случае
A1 0 , то в этом случае
(12) |
A2 q(12) q01 q02 A2 1 A1 1 1 A2F21 2 |
A2 2 |
||
q01 q02 0 1 2 2 q01 q02 2 2 2 |
|
|||
|
2 T1 273 4 T2 273 4 , |
|
|
|
так как из |
условия взаимности A1F12 A2 F21 при |
A1 A2 |
следует, что |
|
F21 F12 , |
F21 1. Иными словами, нагреватель «не замечает» загрузку. |
|||
|
4.2. Задача |
|
|
|
ТЭН с развернутой длиной 600 мм, диаметром оболочки 2rp = 12 мм |
||||
(ri = 3 мм) |
и мощностью 0.5 кВт предназначен |
для |
нагрева воды |
|
(αc = 100 Вт/(м2К)); = 16. |
|
|
|
|
1.Найти температуру спирали и оболочки.
2.Какова будет температура спирали и оболочки, если ТЭН окажется на
воздухе (αc = 15 Вт/(м2К))?
21

4.3.Индивидуальное домашнее задание
Впечи (рис. 4.2) нагревают стальные слитки. Верх печи (свод) занят радиационными нагревателями общей мощностью P = 50, 60, …, 100 кВт. Из-
|
|
Свод печи |
|
|
лучательная способность нагре- |
||||
|
|
|
|
||||||
|
|
|
|
вателей εн = 0.75, боковые стен- |
|||||
|
|
(нагреватели) |
|
|
|||||
|
|
|
|
|
1 м |
ки печи – огнеупорные (адиаба- |
|||
|
Огнеупорные |
|
|||||||
|
|
|
|
|
тические) |
поверхности. |
Печь |
||
|
стенки |
|
|
|
|
прямоугольная |
высотой |
1 м, |
|
|
Под печи (слитки) |
|
|
|
шириной и глубиной 2 м. Слит- |
||||
|
2 м |
ки серые (εс = 0.40, 0.45, …, 0.60) |
|||||||
|
|
|
и расположены на нижней по- |
||||||
|
|
|
|
|
|
||||
|
|
2 м |
верхности |
(на |
поде |
печи). |
|||
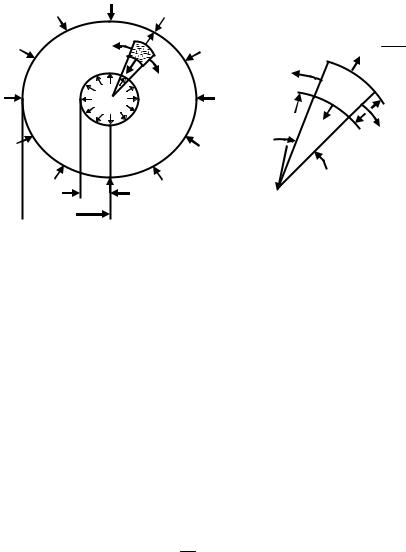
Рис. 4.2 |
Начальная температура слитков |
|
|
300 К. Для этой начальной температуры рассчитать: |
|
а) температуру нагревателя Tн; |
|
б) температуру боковых поверхностей печи Tс;
в) результирующие тепловые потоки для слитков (Фс)р; г) результирующий поток теплообмена излучением между нагревателем и
слитками Ф(н,с).
Исходные данные для вариантов задания приведены в табл. 4.1.
|
|
|
|
|
|
|
|
|
|
|
Таблица 4.1 |
|
|
|
|
|
|
|
|
|
|
|
|
εc |
Ва- |
№ поверхности |
|
|
Результаты |
|
|
Примечания |
|||
|
ри- |
Сли- |
Нагреватель |
T |
T |
|
(Ф ) |
Ф |
|
|
|
|
ант |
ток |
|
|
н |
с |
|
с р |
|
(н,с) |
|
|
№ |
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|
0.4 |
1 |
6 |
1 |
50 |
|
|
|
|
|
|
|
|
2 |
5 |
2 |
60 |
|
|
|
|
|
|
|
|
3 |
4 |
3 |
70 |
|
|
|
|
|
|
|
|
4 |
3 |
4 |
80 |
|
|
|
|
|
|
|
|
5 |
2 |
5 |
90 |
|
|
|
|
|
|
|
|
6 |
1 |
6 |
100 |
|
|
|
|
|
|
|
0.45 |
7 |
1 |
6 |
50 |
|
|
|
|
|
|
|
|
8 |
2 |
5 |
60 |
|
|
|
|
|
|
|
|
9 |
3 |
4 |
70 |
|
|
|
|
|
|
|
|
10 |
4 |
3 |
80 |
|
|
|
|
|
|
|
|
11 |
5 |
2 |
90 |
|
|
|
|
|
|
|
|
12 |
6 |
1 |
100 |
|
|
|
|
|
|
|
22
|
|
|
|
|
|
|
|
|
Окончание табл. 4.1 |
|
|
|
|
|
|
|
|
|
|
|
|
εc |
Ва- |
№ поверхности |
|
Результаты |
|
|
Примечания |
|||
|
ри- |
Сли- |
Нагреватель |
T |
T |
(Ф ) |
Ф |
|
|
|
|
ант |
ток |
|
|
н |
с |
с р |
|
(н,с) |
|
|
№ |
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
0.50 |
13 |
2 |
1 |
50 |
|
|
|
|
|
|
|
14 |
3 |
2 |
60 |
|
|
|
|
|
|
|
15 |
4 |
3 |
70 |
|
|
|
|
|
|
|
16 |
5 |
4 |
80 |
|
|
|
|
|
|
|
17 |
6 |
5 |
90 |
|
|
|
|
|
|
|
18 |
1 |
6 |
100 |
|
|
|
|
|
|
0.55 |
19 |
1 |
2 |
50 |
|
|
|
|
|
|
|
20 |
2 |
3 |
60 |
|
|
|
|
|
|
|
21 |
3 |
4 |
70 |
|
|
|
|
|
|
|
22 |
4 |
5 |
80 |
|
|
|
|
|
|
|
23 |
5 |
6 |
90 |
|
|
|
|
|
|
|
24 |
6 |
1 |
100 |
|
|
|
|
|
|
0.6 |
25 |
1 |
5 |
50 |
|
|
|
|
|
|
|
26 |
2 |
6 |
60 |
|
|
|
|
|
|
|
27 |
3 |
1 |
70 |
|
|
|
|
|
|
|
28 |
4 |
2 |
80 |
939 |
839 |
-80 |
45.7 |
|
|
|
29 |
5 |
3 |
90 |
|
|
|
|
|
|
|
30 |
6 |
4 |
100 |
|
|
|
|
|
|
Указания. Задачу рекомендуется решать матричным методом в MathCad. Недостающие потоки в сводную таблицу заносить в киловаттах, а тем-
пературы в Кельвинах.
F12 |
|
|
|
1 |
X/D |
∞ |
4 |
|
|||
|
|
|
2 |
|
|
|
1 |
|
|
0.8 |
0.6 |
|
|
0.5 |
0.4 |
F |
|
|
0.3 |
12 |
|
|
|
0.1 |
|
0.2 |
0.16 |
|
|
||
|
|
|
|
|
|
0.12 |
|
|
|
|
0.1 |
0.01 |
|
|
|
0.1 |
1 |
|
10 |
|
|
|
Y/D |
|
а |
|
б |
|
|
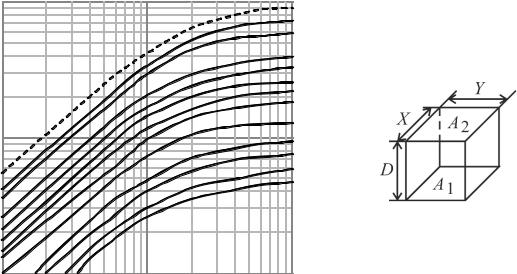
Рис. 4.3 |
|
|
|
|
23 |

F12 |
|
|
|
|
0.5 |
|
/ |
0.1 |
|
|
|
|
||
|
|
Y X |
|
|
0.4 |
|
|
0.2 |
|
|
|
0.4 |
|
|
|
|
|
|
|
0.3 |
|
|
0.6 |
|
|
|
0.8 |
|
|
|
|
|
|
|
|
12 |
|
1.2 |
|
0.2 |
F |
|
1.6 |
|
|
|
|
4 |
2 |
0.1 |
|
|
6 |
|
|
|
10 |
||
|
|
|
|
|
0 |
|
|
|
20 |
|
0.1 |
1 |
|
10 |
|
|
|
|
Z/X |
|
|
а |
|
б |
|
|
|
|
Рис. 4.4 |
Нумерация поверхностей печи производится так, чтобы порядковый номер поверхности нагревателя и слитков совпадал с заданным вариантом.
Угловые коэффициенты ищутся по прилагаемым графикам и с помощью соотношений взаимности.
5. СОПУТСТВУЮЩИЕ ЭЛЕКТРОНАГРЕВУ ЯВЛЕНИЯ 5.1. Термонапряжения
При нагреве внешними и внутренними источниками тепла в изделии по сечению возникает перепад между температурой поверхности Tп и центра Tс
сечения T Tп Tc .
Перепад температуры в плоском теле определяется удельным тепловым сопротивлением (на единицу площади поверхности) r L и зависит от условий нагрева: плотности падающего теплового потока qg, коэффициента теплоотдачи α с поверхности нагреваемого изделия и др.
и зависит от условий нагрева: плотности падающего теплового потока qg, коэффициента теплоотдачи α с поверхности нагреваемого изделия и др.
Во многих случаях перепад температуры по сечению изделия оказывается столь незначительным, что им можно пренебречь и в практических расчетах считать T 0 . Такие изделия называют теплотехнически тонкими. «Тонкое» изделие характеризуется очень малым тепловым сопротивлением, т. е. либо небольшой толщиной нагреваемого слоя L, либо очень высоким коэффициентом теплопроводности . Кроме того, изделия ведут себя как «тонкие» при условии, что отношение теплового сопротивления rλ, характеризу-
24

ющего прохождение тепла в изделии, к тепловому сопротивлению (тоже отнесенному к единице поверхности) r = 1/ , отражающему процесс тепло-
обмена на поверхности изделия, будет меньше 0.25, т. е. |
|
r r = L 0.25 . |
(5.1) |
Приведенное отношение (5.1) сопротивлений для плоского изделия |
|
называют критерием Био (Bi). Таким образом, |
|
Bi = L , |
(5.2) |
где c r – суммарный коэффициент теплоотдачи конвекцией и излу-
чением; L – характерный размер изделия: половина толщины плоского изделия при двустороннем нагреве, радиус цилиндра или шара, определяющий форму изделия.
Если значение критерия Bi ≥ 0.5, то тела в процессе нагрева ведут себя как «массивные» изделия, для которых нельзя пренебрегать перепадом температур по сечению тела. Теплотехнически «тонкое» тело при невысоких температурах может оказаться «массивным» при высоких температурах вследствие роста коэффициента теплоотдачи. Соотношение (5.2) определяет также граничное условие на поверхности. При Bi = 0 – процесс адиабатический.
5.2. Простейшие случаи температурных напряжений |
|
|||||
При нагреве телá равномерно расширяются во все стороны, что приво- |
||||||
дит к относительному изменению объема θ = βΔT, где β – коэффициент объ- |
||||||
емного температурного расширения материала, |
измеряемый в К–1; |
T – из- |
||||
менение температуры тела; T = T, если начало отсчета температуры прирав- |
||||||
нять нулю. При этом каждая сторона малого элемента тела получает темпе- |
||||||
ратурную деформацию |
|
|
|
|
||
|
ε = αΔT, |
|
(5.3) |
σF |
|
|
где α = β/3 |
– коэффициент линейного темпера- |
σl/E |
||||
αΔTl |
||||||
турного расширения материала. |
|
|
|
|||
Если |
нагреваемая |
деталь |
(стержень, |
|
|
|
рис. 5.1) закреплена в жестком корпусе, который |
l |
|
||||
остается холодным, то длина стержня также |
|
|
||||
должна остаться без изменения и в нем возник- |
|
|
||||
нут сжимающие температурные напряжения, ко- |
|
|
||||
торые по закону Гука и с учетом (5.3) определя- |
Рис. 5.1 |
|
||||
ются как |
|
|
|
|
|
|
E E T , |
(5.4) |
25
где E – модуль упругости первого рода или модуль Юнга, характеризующий упругие свойства материала.
Чтобы получить температурные напряжения в пластинке, свободной от внешних усилий, необходимо наложить на напряжения (5.4) такие напряжения, которые вызываются в пластинке растягивающими усилиями интенсивностью ET , распределенными по концам. Эти силы имеют результирую-
c
щую TEdy и на достаточном расстоянии от концов вызывают приблизи-
c
тельно равномерное распределение растягивающих напряжений интенсив-
ностью 1 c TEdy .
2c c
При этом температурные напряжения в пластинке толщиной 2с (рис. 5.2) со свободными концами на достаточном удалении от последних определяются формулой
|
|
|
|
1 |
|
c |
|
|
|
|
|
x |
|
|
TEdy TE . |
|
(5.5) |
|
|
|
2c |
|
||||
|
|
|
|
c |
|
|
||
Считая, например, что температура распределяется по параболическому |
||||||||
закону T T 1 y2 |
c2 , из уравнения (5.5) получим |
|
||||||
0 |
|
|
2 T E T E 1 y2 |
|
. |
|||
|
|
x |
c2 |
|||||
|
|
3 |
n |
0 |
|
|
||
|
|
|
|
|
|
|
|
|
Если распределение температуры Т несимметрично относительно оси х, то следует вновь исходить из сжимающего напряжения (5.4), устраняющего деформацию εx. В несимметричных случаях это напряжение вызывает не только
|
c |
|
результирующее усилие ETdy , но |
|
c |
|
также и результирующий момент |
|
c |
|
ETydy . Чтобы удовлетворить усло- |
|
c |
|
виям равновесия, нужно наложить на |
|
сжимающие напряжения (5.4) равно- |
|
мерное растяжение, определенное так |
Рис. 5.2 |
же, как и ранее, и напряжения изгиба |
26

x |
y |
c , определенные из условия, что момент от усилий, распределенных |
||||||||||||||
по |
|
|
поперечному |
сечению, |
|
должен |
|
равняться |
нулю. |
Тогда |
||||||
c |
y2 |
|
c |
откуда |
|
|
3 |
c |
|
|
3y |
c |
|
|||
|
|
|
dy ETydy 0, |
|
|
|
|
ETydy, x |
|
ETydy. |
|
|||||
|
c |
c |
2c3 |
2c3 |
|
|||||||||||
c |
|
|
c |
|
|
|
c |
|
|
c |
|
|||||
|
|
В результате – полное напряжение |
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
1 |
|
c |
|
|
3y |
c |
|
|
(5.6) |
|
|
|
|
x ET |
|
|
|
ETdy |
|
ETydy. |
|
|||||
|
|
|
|
2c |
2c3 |
|
||||||||||
|
|
|
|
|
|
c |
|
|
c |
|
|
|
||||
При этом предполагается, что пластинка является тонкой в направлении оси z.
5.3. Температурные напряжения в длинном полом цилиндре
Когда стенки цилиндра неравномерно нагреваются, то их элементы расширяются неодинаково, вследствие чего возникают температурные напряжения. В последующем изложении распределение температуры получается симметричным относительно оси цилиндра и постоянным вдоль этой оси. В таком случае деформации цилиндра будут симметричны относительно оси.
Вырежем из цилиндра кольцо с двумя поперечными сечениями, перпендикулярными оси и находящимися одно от другого на расстоянии, равном единице. Из условия симметрии следует, что по граням элемента mnn1m1
(рис. 5.3), выделенного из этого кольца двумя осевыми плоскостями и двумя кольцевыми цилиндрическими поверхностями, не будут действовать касательные напряжения.
Пусть σt означает окружное напряжение, действующее по нормали к граням mm1 и nn1 элемента, и σr – радиальное напряжение, нормальное к грани mn. Это напряжение изменяется с изменением радиуса r, и величина этого изменения на расстоянии dr равняется (dσr/dr)dr. Нормальное радиаль-
ное напряжение по грани m1n1, следовательно, будет σr + ddrσr dr .
Можно допустить, что при деформации эти поперечные сечения остаются плоскими, если взять их на достаточном расстоянии от концов цилиндра (на концах в направлении оси цилиндра напряжения равны нулю); следовательно, относительные удлинения в осевом направлении будут постоянными. Пусть z будет осью цилиндра, w – осевое перемещение по z, остальные обозначения будут теми же, что и на рис. 5.3.
Деформация цилиндра симметрична относительно его оси и состоит из радиального перемещения всех точек стенки цилиндра. Это перемещение посто-
27
янно в окружном направлении, но меняется по радиусу, т. е. является только функцией радиуса. Если u – радиальное перемещение цилиндрической поверхности радиуса r, то перемещение на поверхности радиуса r + dr равняет-
ся u dudr dr . Следовательно, элемент mnn1m1 претерпевает полное удлинение в радиальном направлении, равное (du/dr)dr, а относительное удлинение в
этом же направлении будет r du .
dr
Тогда относительные удлинения в трех перпендикулярных направлениях будут
εz = dw |
=const , εr = du |
, εt =u . |
(5.7) |
dz |
dr |
r |
|
m1 |
n1 |
|
m1 |
m |
|
||
|
n |
m |
|
|
|
|
|
|
|
r |
r |
|
|
|
d |
a |
|
|
|
 b
b
r ddrr dr
n1
dr n
а |
б |
Рис. 5.3
Эти удлинения могут быть выражены в зависимости oт напряжений σz, σr, σt и температурного расширения. Пусть α – коэффициент линейного расширения, а T – прирост температуры сверх равномерной начальной. Температурный прирост меняется только с изменением радиального расстояния r. Удлинения определяются так:
|
z |
z |
|
|
r |
T , |
|
||
|
|
|
|||||||
|
E |
E |
t |
|
|||||
|
|
|
|
|
|||||
|
r |
r |
|
|
|
z |
T , |
(5.8) |
|
|
|
||||||||
|
E |
E |
t |
|
|||||
|
|
|
|
|
|||||
t t r z T .
E E
28

Обозначая через относительное объемное расширение, получаем
|
z |
|
r |
|
|
1 2 |
|
z |
|
r |
|
|
|
3 T . |
(5.9) |
||||||||||||||
|
|
|
|||||||||||||||||||||||||||
|
|
t |
|
|
|
|
E |
|
|
|
|
|
|
t |
|
|
|
||||||||||||
Из уравнений (5.8) и (5.9) находим |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
z |
|
|
|
E |
|
z |
|
|
|
|
|
|
|
|
|
|
|
TE |
, |
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
1 |
|
1 |
2 |
|
1 |
2 |
|
||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TE |
|
, |
|
||||
r |
|
|
|
|
|
|
r |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(5.10) |
|||||
1 |
|
|
1 |
2 |
|
|
1 |
2 |
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
E |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
TE |
. |
|
|||||
|
t |
|
|
|
|
|
|
t |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
1 |
|
1 2 |
|
1 2 |
|
|||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
Уравнения равновесия элемента mnn1m1 (рис. 5.3) получим, проектируя усилия, приходящиеся на элемент, на направление биссектрисы угла dφ. Находим следующее уравнение равновесия:
|
r |
d |
|
|
, |
r rd t drd |
|
r r dr d 0 |
|||
|
|
dr |
|
|
|
или, пренебрегая малыми величинами высшего порядка
t r r ddrr 0 ,
находим
d r |
r t 0. |
(5.11) |
dr |
r |
|
Подстановкой уравнений (5.10) и (5.7) в (5.11) получаем
d 2u |
1 du |
|
u |
|
1 |
dT |
dr2 |
r dr |
|
|
|
|
dr . |
r2 |
1 |
Это уравнение определяет перемещение u для какого-либо частного распределения температуры. Оно может быть переписано в следующем виде:
d 1 d |
ru |
1 |
dT . |
||
|
|
|
|||
|
|
1 |
dr |
||
dr r dr |
|
||||
Интегрирование по r дает
drd ru 11 Tr 2C1r .
Второе интегрирование приводит к решению
u |
1 1 |
r |
Trdr C r C |
|
1 |
, |
(5.12) |
|||
r |
1 |
|
|
2 |
r |
|||||
|
1 |
|
|
|||||||
|
|
|
|
a |
|
|
|
|
|
|
29
где C1 и C2 – постоянные интегрирования, которые должны быть определены
таким образом, чтобы удовлетворить условиям на внутренней и наружной поверхностях цилиндра. Если эти поверхности считать свободными от внешних сил, то условия для определения C1 и C2 выразятся так:
r r a 0 , r r b 0 . |
(5.13) |
Общее выражение для σr получится, если подставить во второе из уравнений
(5.10) εr = dudr и εt =ur , а затем взять вместо u его значение (5.12), что дает
|
|
|
|
E |
|
|
1 |
|
r |
C |
|
|
C |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
|
|
|
||
r |
|
|
|
|
|
|
|
|
Trdr |
|
|
|
|
2 |
|
|
z . |
|
1 |
|
1 r |
2 |
1 |
2 |
r |
1 2 |
|||||||||||
|
|
|
|
|
a |
|
|
|
|
|
||||||||
Тогда из уравнений (5.13) находим
|
|
|
1 |
|
|
|
|
a |
2 |
|
b |
||
|
|
|
|
|
|
|
|
|
|
||||
|
С2 |
|
1 |
|
|
|
|
2 |
a |
2 |
Trdr , |
||
|
|
|
b |
|
|
a |
|||||||
|
1 1 2 |
|
|
|
1 |
|
|
b |
|||||
С1 |
|
|
|
|
|
Trdr z . |
|||||||
|
1 |
|
|
|
|
|
|
|
|
||||
|
|
|
|
b2 a2 a |
|||||||||
Подставляя эти значения в (5.14), получаем общие выражения для σr:
|
|
|
|
E |
|
|
1 |
r |
|
r |
2 |
a |
2 |
|
|
b |
|
|
|||
r |
|
|
|
|
|
Trdr |
|
|
|
|
|
Trdr |
|
, |
|||||||
1 |
|
|
r |
2 |
r |
2 |
(b |
2 |
a |
2 |
|
|
|||||||||
|
|
|
|
|
a |
|
|
|
) a |
|
|
||||||||||
а из уравнения равновесия (5.11) найдем общее выражение для σt:
(5.14)
(5.15)
|
d r |
|
|
|
E |
|
1 |
r |
|
r |
2 |
a |
2 |
|
|
b |
|
|
|||
t r r |
|
|
|
|
Trdr |
|
|
|
|
|
Trdr T |
|
. (5.16) |
||||||||
dr |
1 |
|
|
|
2 |
r |
2 |
(b |
2 |
a |
2 |
|
|
||||||||
|
|
r |
|
a |
|
|
|
) a |
|
|
|||||||||||
Если закон распределения температуры по толщине стенки известен, то можно раскрыть интегралы выражений (5.15) и (5.16) и получить σr и σt для каждого частного случая.
Когда стенки цилиндра имеют температуру Tb на внутренней поверхности и температуру, равную нулю, на наружной, то закон распространения температуры можно представить следующей функцией:
T |
Tb |
|
b |
|
|
|
ln r . |
(5.17) |
|
ln b |
a |
30
