
Sb97281
.pdfE e |
|
e |
|
1 105 |
e |
|
2 10 2 |
В/м . |
z |
z |
|
z |
|||||
|
|
5 106 |
|
|
|
|||
|
|
|
|
|
|
|
Напряженность магнитного поля на внешней поверхности провода находим из закона полного тока в интегральной форме:
H e |
I |
|
94,2 |
e 750 А/м . |
|
|
|||
2 π r |
2 0,02 |
|||
|
2 |
|
|
|
Нормальная к поверхности провода составляющая вектора Пойнтинга:
Sn ez E e H er EH er 2 10 2 750 er15 Вт/м 2.
Тангенс угла есть отношение касательной составляющей вектора Пойнтинга к его нормальной составляющей:
|
|
|
|
|
|
|
|
|
tg |
|
St |
|
|
|
150 |
10 , |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
Sn |
|
|
15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
откуда = 84,3 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
1. В области 0 < r <r1 E = 0; H = 0. Следовательно, S = 0. |
|
|
|
|
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
(r 2 r 2 ) |
|
|
|
|
|
|
2. В области r1 < r < r2 E Et ez |
|
|
; H e H e |
|
1 |
. |
|
|
|||||||||||||||||||||||||||
|
|
|
|
|
2r |
|
|
||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
Поэтому вектор Пойнтинга |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
(r 2 |
r 2 ) |
|
|
(1 105 )2 (r 2 0,012 ) |
|
|
|
1 104 (r 2 0,012 ) |
|
||||||||||||||||||||||
|
|
S er Sr er |
|
|
1 |
|
er |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
er |
|
|
|
|
|
|
|
. |
|||||
|
|
|
2r |
|
|
|
|
|
|
5 106 2r |
|
|
|
|
|
|
|
r |
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
3. В области r2 < r < |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
E er Er |
er |
|
|
|
|
|
; H e H |
e |
I |
|
; |
|
|
|
|
||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
2 r 0 |
|
|
|
|
|
|
|
|
|
|
|
|
2 r |
|
|
|
|
||||||||||
|
|
|
|
|
|
|
S ez S z |
|
ez |
|
|
|
I |
|
|
ez |
|
k |
|
, |
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
|
|
|
|
4 2 |
|
r 2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
r 2 |
|
|
|
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
где |
|
заряд |
на |
единицу |
|
длины |
|
заряженного |
проводника, |
Кл/м; |
|||||||||||||||||||||||||||
k постоянная, Вт. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
Для |
точек, |
лежащих на |
|
поверхности |
|
провода |
известно, |
что |
|||||||||||||||||||||||||||
S |
t |
= S = 1,5 102 |
Вт/м2. Следовательно, |
постоянную k можно получить из |
|||||||||||||||||||||||||||||||||
|
z |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
уравнения, связывающего значение вектора Пойнтинга с радиусом провода
21
S k/r2 , откуда |
k S r 2 1,5102 |
22 10 4 |
6 10 2 Вт . Таким образом, |
|||||
1 |
|
1 |
|
|
|
|
|
|
вектор Пойнтинга вне провода S e |
|
6 10 2 |
Вт/ м2 . |
|||||
z |
r 2 |
|||||||
|
|
|
|
|
|
|||
|
|
|
|
|
|
|
||
S, Вт/м2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
140 |
|
|
|
|
|
|
|
|
|
r1 < r < r2 |
|
|
|
|
|
||
120 |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
||
100 |
|
|
|
|
|
|
|
|
|
|
|
|
|
r > r2 |
|||
|
|
|
|
|
|
|||
80 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
60 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
40 |
|
|
|
|
|
|
|
|
r < r1 |
|
|
|
|
|
|||
|
|
|
|
|
|
|||
20 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
0
1 |
2 |
3 |
4 |
r, см |
Рис. 2.6
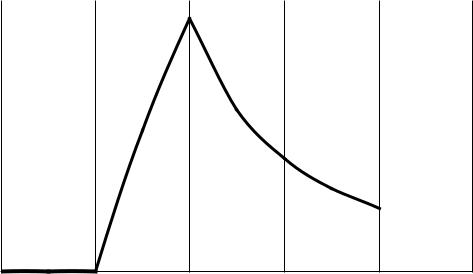
На рис. 2.6 приведена зависимость модуля вектора Пойнтинга в функции расстояния от оси провода для трех областей.
Задача 2.8. Магнитные поля с напряженностями H1(x, y, z) и H2(x, y, z) удовлетворяют равенству rot H1 = rot H2 . Найти связь между величинами H1 и H2.
Решение. Поскольку rot grad = 0, где скалярная функция, получаем одно из возможных решений:
H1 = H2 + grad .
22
Содержание |
|
1. Электростатическое поле ................................................................................. |
3 |
Задача 1.1 ……………………………………………………………….. 3 |
|
Задача 1.2 ……………………………………………………………….. 4 |
|
Задача 1.3 ……………………………………………………………….. 6 |
|
Задача 1.4 ……………………………………………………………….. 6 |
|
Задача 1.5 ……………………………………………………………….. 7 |
|
Задача 1.6 ……………………………………………………………….. 8 |
|
Задача 1.7 ……………………………………………………………….. 8 |
|
Задача 1.8 ………………………………………………………………..11 |
|
Задача 1.9 ………………………………………………………………..11 |
|
2. Магнитное поле постоянного тока ................................................................. |
12 |
Задача 2.1 ………………………………………………………………..12 |
|
Задача 2.2 ………………………………………………………………..13 |
|
Задача 2.3 ………………………………………………………………..14 |
|
Задача 2.4 ………………………………………………………………..16 |
|
Задача 2.5 ………………………………………………………………..17 |
|
Задача 2.6 ………………………………………………………………..19 |
|
Задача 2.7 ………………………………………………………………..20 |
|
Задача 2.8 ………………………………………………………………..22 |
|
23
Печенков Андрей Юрьевич, Галунин Сергей Александрович
Решение задач электростатического поля и магнитного поля постоянного тока
Учебно-методическое пособие
Редактор И. Г. Скачек
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Подписано в печать 25.10.18. Формат 60×84 1/16. Бумага офсетная. Печать цифровая. Печ. л. 1,5.
Гарнитура «Times New Roman». Тираж 45 экз. Заказ 167.
––––––––––––––––––––––––––––––––––––––––––––––––––––––––––
Издательство СПбГЭТУ «ЛЭТИ» 197376, С.-Петербург, ул. Проф. Попова, 5
