Sb97281

6. Циркуляция вокруг изображенного контура не равна нулю (рис. 1.5, е), поэтому rot F 0. Так как векторы сходятся к центру со всех сторон, то div F 0.

Задача 1.8. Найти электрическое поле бесконечно длинного заряженного проводника.

Решение. Пусть заряд на единицу длины заряженного проводника равен [Кл/м] и его можно считать практически постоянным, так как концы проводника находятся в бесконечности. В силу симметрии вектор напряженности электрического поля E в окружающей среде, имеющей постоянную абсолютную диэлектрическую проницаемость , всюду направлен радиально. Его величина Er будет одной и той же во всех точках любой цилиндрической поверхности произвольного радиуса r, ось которой совпадает с заряженной осью. Применим теорему Гаусса, беря в качестве расчетной поверхности боковую поверхность цилиндра единичной длины с радиусом r. Поток вектора D через торцевые поверхности цилиндра равен нулю, поскольку векторы D и E им параллельны. Поэтому

Dr 2 r 1 Er 2 r 1 ,

откуда

Er 2 r .

Задача 1.9. Найти поле шара с радиусом R и абсолютной диэлектрической проницаемостью r, заряженного с постоянной объемной плотностью и находящегося в воздухе.

Решение. Сферическая поверхность радиусом r (r > R) заключает в себе заряд q, равный 43 R3 . Из теоремы Гаусса для поля вне шара получаем:

Для точек внутри шара результат будет иным. Заряд, находящийся внут-

ри сферической поверхности радиусом r (r < R), равен 43 r3 . Поэтому для этой поверхности

11

2. МАГНИТНОЕ ПОЛЕ ПОСТОЯННОГО ТОКА Задача 2.1. По медному проводнику радиусом а = 0,5 см протекает по-

стоянный ток I = 50 А. Определите интенсивность магнитного поля (значения H и B) в точках, удаленных от оси проводника на расстояние r1 = 0,2 см; r2 = 0,5 см; r3 = 1,0 см.

Решение. Найдем значения H и B на расстоянии r1 = 0,2 см от оси проводника. По закону полного тока находим ток i, протекающий через поверхность, ограниченную контуром радиусом r1:

Hdl i H 2r1. l

Так как в проводнике радиусом а протекает постоянный ток, то его плотность J в каждой точке сечения проводника имеет постоянное значение:

J I .a2

Учитывая это условие, выразим ток i, протекающий через поверхность Sr1, ограниченную контуром радиусом r1, через плотность тока:

Поскольку это один и тот же ток, то можем приравнять полученные выражения:

Найдем H и B на расстоянии r2 = 0,5 см от оси проводника (т. е. на его поверхности). Из закона полного тока и связи между B и H имеем:

12

Найдем H и B на расстоянии r3 = 1,0 см от оси проводника (т. е. снаружи проводника):

Hdl I H 2r3; l

B 0 r H 4 10 7 1 796 10 10 4 Тл.

Задача 2.2. Интегрируя уравнение rot H = J и принимая абсолютную магнитную проницаемость равной 0 всюду, рассчитайте напряженность магнитного поля внутри и вне бесконечно длинной трубы с внутренним и наружным радиусами Rвн = 5 мм, Rнар = 8 мм с током I = 20 A при условии постоянства плотности тока в трубе.

Решение. Внутри трубы тока нет, следовательно, нет и магнитного поля. Плотность тока в трубе определяется выражением

Обозначим текущий радиус через Rтек. В стенке трубы выполняется ус-

ловие Rвн Rтек Rнар.

Ток, текущий через поверхность, ограниченную внутренним и текущим радиусами, определяется как

С другой стороны, ток, текущий через поверхность, ограниченную внутренним и текущим радиусами, можно найти и из закона полного тока

Hdl i H 2 Rтек . l

Так как это один и тот же ток i, то можем приравнять полученные выражения и найти закон изменения H по толщине трубы:

13

Найдем H на расстоянии Rнар + r от оси проводника (т. е. вне проводни-

ка):

Hdl I H 2 (Rнар r); l

300

200

100

0

1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 r, мм

Рис. 2.1

На рис. 2.1 приведено распределение напряженности магнитного поля внутри трубы, в ее стенке и снаружи трубы.

Задача 2.3. По внутреннему проводнику бесконечно длинного коаксиального кабеля течет постоянный ток I1 = 20 A. По наружному проводнику течет ток I2 = I1. Радиус внутреннего проводника R1 = 2 мм. Внутренний радиус наружного проводника R2 = 6 мм. Внешний радиус наружного проводника R3 = 8 мм. Рассчитайте: 1) напряженность магнитного поля внутри внутреннего проводника; 2) напряженность магнитного поля в зазоре между проводниками; 3) напряженность магнитного поля внутри наружного проводника; 4) напряженность магнитного поля снаружи коаксиального кабеля.

Решение:

1. В задаче 2.1 было найдено распределение напряженности магнитного поля по радиусу проводника. В обозначениях настоящей задачи оно выглядит следующим образом:

14

где Rтек – текущий радиус, причем 0 Rтек R1.

2. При R1 Rтек R2 распределение напряженности магнитного поля будет иметь вид

H I1 .

2Rтек

3. Рассмотрим случай R2 Rтек R3, I2 = I1.

Плотность тока в наружном проводнике определяется как

Ток, текущий в наружном проводнике по сечению с текущим радиусом Rтек (в этом случае R2 Rтек R3):

Распределение напряженности магнитного поля по радиусу наружной жилы бесконечно длинного коаксиального кабеля имеет вид

4. Рассмотрим случай Rтек R3. Распределение напряженности магнитного поля имеет вид

H I1 I1 0.

2Rтек

На рис. 2.2 построено распределение напряженности магнитного поля внутри наружного и внутреннего проводников, в зазоре между проводниками, снаружи коаксиального кабеля. Выделены толщины внутреннего и наружного проводников. Как и следовало ожидать, во внутреннем проводнике распределение H(r) носит линейный характер. В диэлектрике между проводниками распределение H(r) обратно пропорционально радиусу.

15

H, А/м 1600 1200 800 400

0

1 2 3 4 5 6 7 8 9 r, мм

Рис. 2.2

Внутри наружного проводника распределение напряженности магнитного поля носит сложный нелинейный характер. Напряженность магнитного поля снаружи коаксиального кабеля равна нулю.

Задача 2.4. Вычислите ЭДС в движущейся рамке в тот момент, когда она находится в положении, показанном на рис. 2.3, а. Укажите направле-

ние тока в рамке.

16

изменение потока через рамку за время dt равно d B1 B2 bvdt.

Отсюда

ЭДС d B1 B2 bv. dt

Данное выражение справедливо для петли любой формы, движущейся любым способом.

Найдем значения B1 и B2, исходя из условий задачи и используя закон полного тока в интегральной форме:

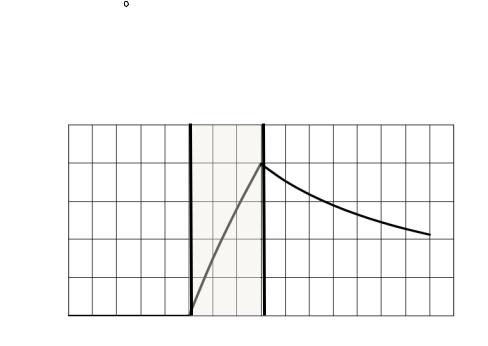
Ток в рамке на рис. 2.3, а задания направлен по часовой стрелке, так как по закону Ленца индуцированный в рамке ток создает через нее некоторый поток, противодействующий изменению магнитного потока.

Задача 2.5. Вдоль длинного цилиндрического стального провода протекает постоянный ток. Радиус провода r0 = 1 см. Относительная магнитная проницаемость стали r = 50. Средой, окружающей провод, является воздух. Проекция векторного магнитного потенциала на ось z меняется в функции расстояния от оси провода по закону A1 = 6,28r2 Вб/м внутри провода и

A2 = 25,1 10 6 ln r 6,28 10 4 Вб/м вне провода.

Найдите законы изменения модулей напряженности поля H и вектора намагниченности М в функции расстояния от оси провода. Постройте графи-

ки функций H = f1(r), H = f2(r), М = f3(r).

Решение. Так как B = rot A, то модуль вектора магнитной индукции внутри и вне провода найдем из выражений

B2 B2e rote A2 Aez2r

17

Определим модуль напряженности магнитного поля внутри и вне провода:

Так как индукция B = 0(H + M), то модуль вектора намагниченности внутри и вне провода

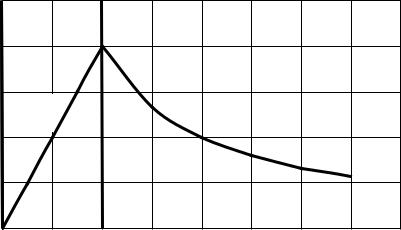
На рис. 2.4 построены графики функций H1 = f1(r) и H2 = f2(r).

Н, А/м

2000

1500

1000

500

0

Рис. 2.4

18

19

Учитывая, что токи Iж и Iоб равны, найдем выражение для r2 и его значение:

r2 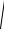r02 r12 (5 10 3)2 (1 10 2 )2 1,118 10 2 м.

Плотность тока в жиле и оболочке кабеля:

Найдем зависимость модуля магнитной индукции в функции расстояния от оси кабеля.

Область 0 r r0:

Задача 2.7. Вдоль цилиндрического прямолинейного полого металлического провода ( = 5 106 Ом 1 м 1), расположенного в воздухе, протекает постоянный ток I = 94,2 А. Внутренний радиус провода r1 = 1 см, внешний радиус r2 = 2 см. Известно, что касательная составляющая вектора Пойнтинга к внешней поверхности провода St = 1,5 102 Вт/м2.

Найдите угол , который составляет вектор Пойнтинга с нормалью к поверхности провода. Постройте зависимость модуля вектора Пойнтинга в функции расстояния от оси провода для трех областей: 1) внутри провода; 2) в теле провода; 3) вне провода.

Решение. Найдем плотность тока в теле провода:

Напряженность электрического поля в теле провода найдем из закона Ома в дифференциальной форме:

20