
tFAnB9BaL5
.pdf
МИНОБРНАУКИ РОССИИ
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»
ОСНОВЫ ТЕОРИИ НАДЕЖНОСТИ
Методические указания к практическим занятиям
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2014
УДК 519.6 + 62.192
Основы теории надежности: метод. указания к практ. занятиям / сост.: В. А. Смирнова, А. В. Чирина. СПб.: Из-во СПбГЭТУ «ЛЭТИ», 2014. 24 с.
Содержат типовые задачи по теории надежности с решениями, задачи для самостоятельного решения, а также основные сведения по теории надежности и связанным с ней областям математической статистики.
Предназначены студентам специальности «Приборостроение».
Утверждено редакционно-издательским советом университета
вкачестве методических указаний
©СПбГЭТУ «ЛЭТИ», 2014
2
1. ОСНОВНЫЕ ПОНЯТИЯ ТЕОРИИ НАДЕЖНОСТИ
Надежность – это свойство объекта сохранять во времени в установленных пределах все параметры, обеспечивающие выполнение требуемых функций в заданных условиях эксплуатации.
Уровень надежности позволяет развивать технику по основным направлениям, включающим автоматизацию производства, интенсификацию рабочих процессов и транспорта, экономию материалов и энергии.
В теории надежности рассматриваются следующие объекты.
Изделие – единица продукции, выпускаемая данным предприятием (например, подшипник, ремень, станок).
Элемент – простейшая при данном рассмотрении составная часть изделия. В задачах надежности элемент может состоять из многих деталей.
Система – совокупность совместно действующих элементов, предназначенных для самостоятельного выполнения заданных функций. Понятия «элемент» и «система» трансформируются в зависимости от поставленной задачи.
Изделия делятся на восстанавливаемые и невосстанавливаемые.
Надежность изделия характеризует следующие основные состояния:
–работоспособность – состояние изделия, при котором оно может нормально выполнять заданные функции. Работоспособность не касается требований, непосредственно не влияющих на эксплуатационные показатели;
–исправность – состояние изделия, при котором оно удовлетворяет не только основным, но и вспомогательным требованиям;
–неисправность – состояние изделия, при котором оно не соответствует хотя бы одному из требований технической документации. Различают неисправности, приводящие и не приводящие к отказам;
–отказ – событие, заключающееся в полной или частичной утрате работоспособности.
Причины отказов делятся на случайные и систематические. Случайные причины – непредусмотренные перегрузки, дефекты матери-
ала и погрешности изготовления. Случайные факторы вызывают отказы при неблагоприятном стечении обстоятельств.
Систематические причины – это закономерные явления, вызывающие постепенное накопление повреждений: влияние среды, времени, температуры, обслуживания.
В соответствии с этими причинами и характером развития и проявления отказы делят на внезапные (поломки от перегрузок и заедания) и постепенные (износ, старение, коррозия, залипание).
3
Внезапные отказы вследствие своей неожиданности более опасны, чем постепенные.
Организация и оптимизация ремонта и профилактической замены оборудования также являются предметом изучения теории надежности, однако небольшой объем настоящих методических указаний не позволяет остановиться на этих темах. Поэтому рекомендуем обратиться к публикациям [1]–[3] для более глубокого изучения предмета. Множество задач как на эти темы, как и на сюжеты, рассмотренные в данных методических указаниях, можно найти в [4].
2. КОЛИЧЕСТВЕННЫЕ ПОКАЗАТЕЛИ НАДЕЖНОСТИ
P(t) – вероятность безотказной работы в течение времени t, или функ-
ция надежности. Функция P(t) является невозрастающей (убывающей).
Обычно предполагают, что в момент времени t = 0 отказ не происходит, но за бесконечное время обязательно про-
изойдет, т. е. P(0) = 1, P(+∞) = 0 .
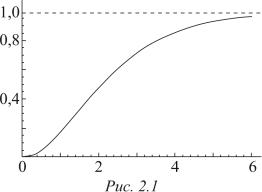
Q(t) – вероятность отказа в течение времени t. Типичный график функции Q(t)
приведен на рис. 2.1.
Поскольку отказ и безотказная работа в течение времени t являются взаимодополняющими событиями, верны формулы
P(t) = 1 − Q(t) , P(t) = 1 − Q(t) , Q(0) = 0 , Q(+∞) = 1 и функция Q(t) является неубывающей (возрастающей).
f (t) – плотность вероятности отказа в течение времени t. f (t) и Q(t)
связаны формулами:
f (t) = Q′(t);
t
Q(t) = ∫ f (t) dt.
0
λ(t) – плотность интенсивности отказов в момент времени t. λ(t)
представляет собой отношение плотности вероятности отказов к вероятности безотказной работы в течение времени t:
|
f (t) |
|
|
f (t) |
|
|
′ |
|
λ(t) = |
= |
|
= |
|
Q (t) |
. |
||
|
|
|
|
|
||||
|
P(t) 1 |
− Q(t) 1 |
− Q(t) |
|||||
4
Среднее время наработки до отказа, т. е. математическое ожидание времени, прошедшего с начала работы изделия до первого отказа:
|
|
+∞ |
|
|
|
M = ∫ |
tf (t) dt. |
|
|
0 |
|
Если, как предполагалось ранее, |
Q(0) = 0 и Q(+∞) = 1, то с учетом зави- |
||
симости |
′ |
можем с помощью интегрирования по частям получить |
|
f (t) = Q (t) |
|||
следующее выражение для М: |
|
||
|
|
+∞ |
+∞ |
|
|
M = ∫ P(t) dt = ∫ (1 − Q(t))dt. |
|
|
|
0 |
0 |
Функция вероятности безотказной работы однозначно выражается через плотность интенсивности отказов. Поскольку
λ(t) = (− ln(1 − Q(t)))′ = (− ln(P(t)))′ ,
имеем
t
− ln(1 − Q(t)) = ∫ λ(t) dt
0
и, следовательно, получим основное уравнение теории надежности:
|
− |
t |
|
|
∫ |
|
|
1 − Q(t) = P(t) = exp |
|
λ(s) ds . |
|
|
|
0 |
|
Здесь приведены важнейшие характеристики надежности и связи между |
|||
ними; в литературе также упоминаются и некоторые другие характеристики. Задача 1. Вероятность безотказной работы в течение времени t задана
формулой |
|
|
|
|
|
|
|
P(t) = |
1 |
|
. |
|
|
||
|
|
|
|
|
|||
(1 + t )2 |
|
|
|||||
Найти f (t), Q(t), λ(t), М. |
|
|
|
|
|
|
|
Решение. По определению |
|
|
|
|
|
|
|
Q(t) = 1 − P(t) = |
1 − |
|
|
1 |
|||
|
|
|
|||||
|
+ t)2 |
||||||
|
|
(1 |
|||||
и |
|
|
|
|
|
|
|
′ |
|
|
2 |
|
|
||
|
|
(1 + t)3 . |
|||||
f (t) = Q (t) = |
|
||||||
5
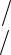
Теперь можем вычислить:
λ(t) = |
f (t) |
= |
2 (1 + t)3 |
= |
|
|
2 |
|
||||
|
1 (1 + t)2 |
|
|
+ t |
||||||||
|
P(t) |
|
1 |
|||||||||
и |
|
|
|
|
|
|
|
|
|
|
|
|
+∞ |
|
|
+∞ |
|
dt |
|
|
|||||
M = ∫ P(t) dt = |
∫ |
|
= 1. |
|||||||||
|
|
|
|
|
||||||||
(1 |
+ t)2 |
|||||||||||
0 |
|
|
|
0 |
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|||
Задача 2. Плотность интенсивности отказов задана формулой λ(t) = 4t.
Найти P(t), Q(t), f (t).
Решение. Вычислим сначала
t
∫ λ(t) dt = 2t2.
0
Теперь можем найти:
P(t) = exp(−2t2 ),
Q(t) = 1 − exp(−2t2 )
и
f(t) = Q′(t) = 4t exp(−2t2 ).
3.ПОКАЗАТЕЛЬНОЕ РАСПРЕДЕЛЕНИЕ. ПЕРИОД ВНЕЗАПНЫХ ОТКАЗОВ
Показательное распределение играет особую роль в теории надежности. Пусть a > 0 – константа, и пусть плотность интенсивности отказов задается формулой λ(t) = λ , т. е. не зависит от времени работы изделия. Тогда
|
P(t) = exp(−λt ), |
||||
|
Q(t) = 1 − exp(−λt ), |
||||
|
f (t) = λexp(−λt ) |
||||
и |
|
|
|
|
|
+∞ |
+∞ |
exp(−λt ) dt = |
1 |
|
|
M = ∫ |
P(t) dt = ∫ |
. |
|||
|
|||||
0 |
0 |
|
λ |
||
|
|
|
|||
6

Показательное распределение обладает множеством свойств, делающих его удобным для применения. В первую очередь это, конечно, простота вычисления основных характеристик. Сформулируем основное свойство показательного закона – свойство отсутствия последействия.
Пусть вероятность отказа в течение времени t распределена в соответствии с показательным законом для некоторого параметра λ . Тогда вероятность P(t, t + τ) безотказной работы до момента t + τ при условии,
что изделие проработало безотказно до момента t, зависит только от τ, но не от t. Иными словами, нет разницы между новым изделием и изделием, проработавшим безотказно до момента t.
Докажем это утверждение. Напомним, что условная вероятность события A при условии, что произошло событие B, по определению равна
P( A | B) = P( AB) .
P(B)
Примем за A событие «безотказная работа до момента t + τ», а за B – событие «безотказная работа до момента t ». Тогда событие AB совпадет с событием A (поскольку A B ) и
P(t, t + τ) = |
P(t + τ) |
= |
exp(−λ(t + τ)) |
= exp(−λτ), |
|
P(t) |
exp(−λt ) |
||||
|
|
|
что и требовалось доказать.
Это свойство является также характеристическим свойством показа-
тельного распределения: если для любых τ и t P(t, t + τ) не зависит от t, то
распределение является показательным с некоторым параметром λ. Это утверждение оставим без доказательства.
Показательное распределение описывает период внезапных отказов, когда старение еще не сказывается на работе изделия.
Пример. Пусть отказ в космическом корабле может возникнуть только из-за попадания в него достаточно крупного метеорита. Если предположить, что метеориты распределены равномерно в пространстве и во времени, то ясно, что вероятность попадания метеорита в корабль в данном интервале времени не зависит от того, попадали или нет метеориты в корабль в прошлом. Следовательно, закон в этом случае экспоненциальный.
Если, как обычно, λt < 0,1, то формула для вероятности безотказной рабо-
ты упрощается в результате разложения в ряд и отбрасывания малых членов:
7

P(t) =1 - λt + (λt )2 - (λt )3 +…» λt. 2! 3!
Задача 3. Оценить вероятность P(t) отсутствия внезапных отказов механизма в течение t = 10 000 ч, если интенсивность отказов составляет λ =10−8 ч.
Решение. Так как λt =10−8 ×104 =10−4 , то воспользуемся приближенной
зависимостью
P(t) »1 - λt =1 -10−4 = 0,9999.
Задача 4. Время работы элемента до отказа подчинено показательному закону с параметром λ = 2,5 ×10−5 ч.
Вычислить количественные характеристики элемента P(t), Q(t), f (t) и
М для t = 1000 ч.
Решение:
e−λt = e−0,025 » 0,9753;
P(t) = 0,9753; Q(t) = 1 − 0,9753 = 0,0247; f (t) = 2,5 ×10−5 × 0,9753 » 2, 438 ×10−5;
M = |
|
1 |
|
= 40 000 |
ч. |
|
×10 |
−5 |
|||
2,5 |
|
|
|
||
4.ДРУГИЕ РАСПРЕДЕЛЕНИЯ, ИСПОЛЬЗУЕМЫЕ
ВТЕОРИИ НАДЕЖНОСТИ
Распределение Вейбулла с положительными параметрами (λ, θ). Это рас-
пределение было предложено для описания усталостных отказов. Для него
P(t) = exp(-(λt )θ ), t > 0.
Параметр θ называется параметром формы, а λ – параметром масшта-
ба. При θ = 1 распределение Вейбулла превращается в показательное. Частный случай распределения Вейбулла при θ = 2 носит название закона Рэлея. График плотности Рэлея см. на рис. 4.1.
Задача 5. Найти плотность распределения отказов и плотность интенсивности отказов для распределения Вейбулла. Построить их графики при λ = 1, θ = 2 .
8

Решение:
f (t) = −P′(t) = θλ(λt )θ−1 exp(−(λt )θ ),
λ(t) = λθ(λt )θ−1.
Для закона Рэлея с параметром масштаба 1 получим
f (t) = 2t exp (−t2 ),
λ(t) = 2t.
Для вычисления математического ожидания распределения Вейбулла требуется определить новую функцию, которая широко используется в математике и приложениях. Гамма-функция определяется следующим образом:
+∞
Γ(z) = ∫ t z−1e−t dt, z > 0
0
и обладает замечательным свойством: для любого z > 0
Γ(z + 1) = zΓ(z).
В частности, Γ(n) = (n −1)! для всех натуральных n.
Задача 6 (для самостоятельного решения). Доказать, что, если отказы распределены по закону Вейбулла, то среднее время до отказа вычисляется по формуле
M = |
1 |
|
+ |
1 |
|
|
Γ 1 |
|
. |
||
λ |
|
||||
|
|
|
θ |
||
Задача 7 (для самостоятельного решения). При каких значениях θ плотность интенсивности отказов является возрастающей функцией?
С помощью гамма-функции определим и следующее семейство распределений. Пусть, как и раньше, λ и θ – положительные параметры. Опреде-
лим плотность распределения отказов формулой
f (t) = λ(λt )θ−1 e−λt .
Γ(θ)
Как и в предыдущем случае, θ – параметр формы, а λ – масштаба; как и раньше, при θ = 1 распределение превращается в показательное. Распределения с плотностями такого вида называются гамма-распределениями. Графики гамма-плотнос- тей показаны на рис. 4.2 (параметр формы 2) и 4.3 (параметр формы 0,5).
Частным случаем гамма-распределений являются суммы независимых одинаково распределенных случайных величин, каждая из которых имеет по-
9

казательный закон распределения. Сумма n таких случайных величин имеет гамма-распределение с параметром формы n и таким же параметром масштаба λ, как у исходных показательных распределений. Математическое ожида-
ние такой случайной величины, очевидно, равно n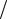 λ.
λ.
Можно доказать, что при θ > 1 плотности интенсивности отказов для распределения Вейбулла и гамма-распределения являются при всех t > 0 возрастающими функциями. Распределения, которые обладают этим свойством, называются ВФИ-распределениями (сокращение от «возрастающая функция интенсивности»). Свойство ВФИ можно естественным образом интерпретировать как старение или износ. Таким образом, ВФИ-распределения описывают поведение изделий в период систематических отказов, связанных со старением. Можно доказать (см. [5], [6]), что сумма, максимум и минимум набора случайных величин, имеющих ВФИ-распределения, также являются ВФИ. Отсюда следует, что системы, составленные из элементов с ВФИ, тоже имеют ВФИ-распределения безотказной работы.
5. ПОВЕДЕНИЕ СИСТЕМЫ В ИЗНОСОВЫЙ ПЕРИОД. НОРМАЛЬНОЕ РАСПРЕДЕЛЕНИЕ
Для описания поведения системы в период постепенных отказов период часто применяют нормальное, или гауссовское распределение. Оно играет ключевую роль в теории вероятностей, в математической статистике и в их приложениях. Применение этого распределения обычно связано с воздействием множественных факторов, которые суммируются. Плотность нормального распределения зависит от двух параметров: произвольного веще-
ственного m и положительного σ2: |
|
|
|
|
|
||
f (t) = |
1 |
|
|
− |
(t − m)2 |
||
|
|
|
exp |
|
. |
||
|
|
|
2σ2 |
||||
|
σ 2π |
|
|
|
|
||
