tFAnB9BaL5

Функция распределения нормального закона не является элементарной, однако она хорошо изучена и представлена в статистических таблицах и вычислительных пакетах. Для функции надежности пользуются выражением

– функция Лапласа, или функция ошибок. Будьте внимательны: в вычислительных пакетах и таблицах функцией ошибок часто называют функцию

Легко видеть (докажите!), что erf (t) = 2Φ(t 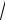2 ).

Задача 8. Время безотказной работы элемента подчинено нормальному распределению с параметрами m = 90 ч, σ = 30 ч.

Найти вероятность того, что элемент проработает безотказно в течение 60 ч.

Решение:

Сумма независимых нормально распределенных случайных величин также является нормально распределенной, при этом среднее значение суммы равно сумме средних значений исходных величин, а дисперсия – сумме дисперсий.

Сумма квадратов n независимых стандартных (т. е. имеющих парамет-

ры m = 0, σ2 = 1) нормальных случайных величин имеет гамма-распределение с параметром формы n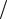2 и параметром масштаба 1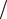2. Такие распределения называются распределениями хи-квадрат с n степенями свободы и обозна-

чаются χ2n.

Плотности Вейбулла с параметром формы 3,3 очень хорошо приближаются гауссовскими плотностями.

Заметим, что для нормального закона не выполняется условие равенства функции надежности единице в начальной точке. В литературе (см., например, [3]) упоминаются распределения, связанные с нормальным законом, для

11

которых это условие выполнено. Это усеченное нормальное и логарифмически нормальное (логнормальное) распределения.

6. ОЦЕНИВАНИЕ ПАРАМЕТРОВ НАДЕЖНОСТИ ПО ЭКСПЕРИМЕНТАЛЬНЫМ ДАННЫМ

Пусть имеется N элементов, из которых за время t безотказно прорабо-

тало N p элементов, а отказало – n элементов. Тогда оценка вероятности без-

отказной работы за время t

P*(t) = N p N ,

а оценка вероятности отказа за то же время составит Q*(t) = n N =1 - P*(t).

Задача 9. Из 1000 элементов за один час работы отказало 30 элементов. Найти оценки вероятностей безотказной работы и отказа в течение часа.

Решение:

Для оценки частоты отказов и интенсивности отказов надо знать кроме количества отказов с начала работы до момента t также ∆n – количество от-

казов в интервале (t, t + τ) и среднее количество элементов, исправно рабо-

тавших в интервале (t, t + τ).

Задача 10. На испытание было поставлено 1000 ламп. В течение первых 3000 ч отказало 80 ламп, а за следующие 1000 ч – еще 50 ламп.

Оценить частоту и интенсивность отказов ламп в интервале времени

3000…4000 ч.

Решение. В данном случае t = 3000, N = 1000, N p = 1000 − 80 = 920,

τ = 1000, n = 50, Ncp = 0,5 × (1000 - 80 +1000 - 80 - 50) = 895. Подставим эти

значения в формулы, приведенные ранее:

12

7. НАДЕЖНОСТЬ СИСТЕМ С РЕЗЕРВИРОВАНИЕМ. МАСШТАБ РЕЗЕРВИРОВАНИЯ

Уровень, на котором производится резервирование системы, называется

масштабом резервирования.

В случае нагруженного резерва резервные элементы подключаются па-

раллельно основным.

В случае ненагруженного резерва резервные элементы включаются только при отказе основных. При этом будем считать, что переключение все-

гда происходит абсолютно надежно. В реальности так происходит не всегда,

и существуют модели, учитывающие ненадежность переключения.

Существуют и другие виды резервирования – например теплое резерви-

рование, при котором резервные элементы до отказа основных работают в облегченном режиме. Однако для простоты будем рассматривать только пер-

вые два вида резервирования.

При резервировании системы можно резервировать либо отдельные элементы системы, либо блоки, входящие в систему, либо всю систему в це-

лом.

Выясним, как масштаб резервирования влияет на надежность. Докажем,

что как для нагруженного, так и для ненагруженного резерва любое

укрупнение масштаба резервирования уменьшает надежность системы.

Всякое укрупнение масштаба резервирования можно представить себе так: имеется m частей системы, и каждая часть имеет n подобных себе ча-

стей. Эти части образуют в системе некоторый блок. Объединив все первые,

вторые и т. д. резервные части, получим n резервных блоков, подобных рас-

сматриваемому. Нужно доказать, что надежность системы при таком объеди-

нении резерва уменьшается.

Всякое объединение резервов частей системы можно представить как последовательное объединение пар частей, следовательно, достаточно рас-

смотреть систему, состоящую из двух частей.

13

Интересно заметить, что этот вывод не зависит от закона надежности элемента.

Итак, чем крупнее масштаб резервирования, тем меньше надежность.

8. РАСЧЕТ НАДЕЖНОСТИ ДЛЯ СЛУЧАЯ НАГРУЖЕННОГО РЕЗЕРВА

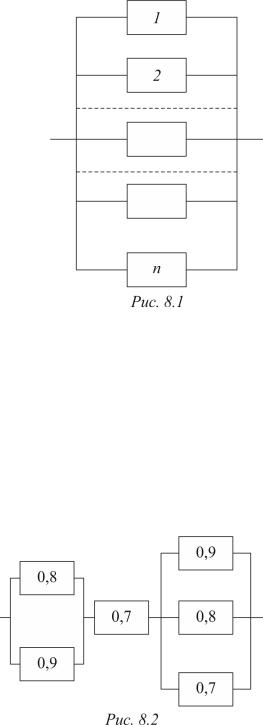
Пусть некоторый элемент резервируется группой из n −1 дополнительных элементов (рис. 8.1).

Пусть вероятность отказа за время t каждого из элементов независимо от других равна Qk (t), k = 1, ..., n, а функция надежности каждого из эле-

ментов равна Pk (t), k = 1, ..., n. Так как элементы независимы, подключены параллельно и отказ блока произойдет в том и только том случае, если откажут все элементы, вероятность отказа тогда выражается формулой

n

Q(t) = ∏ Qk (t). k =1

Соответственно, надежность системы вычисляется по формуле

n

P(t) = 1 − ∏ (1 − Pk (t)). k =1

Если характеристики надежности всех элементов одинаковы, то формулы заметно упрощаются:

Q(t) = (Q1(t))n ,

P(t) = 1 − (1 − P (t))n .

1

Задача 11. Схема устройства дана на рис. 8.2, где обозначены вероятности безотказной работы в течение заданного времени для каждого из элементов.

Найти вероятность безотказной работы устройства в течение этого же времени.

Решение. Система состоит из трех блоков, соединенных последовательно (обозна-

15

чим их А, В, С). Вероятность безотказной работы системы равна произведению вероятностей безотказной работы всех трех блоков. Вычислим эти вероятности:

PA(t) = 1 − (1 − 0,8)(1 − 0,9) = 1 − 0,02 = 0,98;

PB (t) = 0,7;

PC (t) = 1 − (1 − 0,9)(1 − 0,8)(1 − 0,7) = 1 − 0,006 = 0,994.

Таким образом, P(t) = 0,98 × 0,7 × 0,994 » 0,682.

9. РАСЧЕТ НАДЕЖНОСТИ В СЛУЧАЕ НЕНАГРУЖЕННОГО РЕЗЕРВА

Для ненагруженного резерва расчет надежности существенно усложняется, так как времена отказов в этом случае складываются и приходится иметь дело со сверткой функций распределений вероятностей. В случае показательного распределения отказов можно применить упрощенную приближенную формулу:

n

∏ Qk (t)

В [1] доказывается, что в типичных случаях эта формула либо хорошо приближает функцию распределения отказов системы с ненагруженным резервом, либо служит достаточно хорошей верхней оценкой (например, для ВФИ-распределений).

Задача 12. Вернемся к рис. 8.2. Будем теперь считать, что для каждого блока действует модель ненагруженного резерва, а распределения времени безотказной работы имеют показательные распределения.

Найти вероятность безотказной работы устройства в течение заданного времени.

Решение. Воспользуемся приближенной формулой для каждого блока:

≈ − (1 − 0,8)(1 − 0,9) =

P (t) 1 0,99;

A

2! PB (t) = 0,7;

≈ (1 − 0,9)(1 − 0,8)(1 − 0,7) =

PC (t) 0,999. 3!

Перемножив эти вероятности, получим окончательный ответ: 0,692. Это, очевидно, больше, чем в случае нагруженного резерва.

16

10. ПРОВЕРКА СТАТИСТИЧЕСКИХ ГИПОТЕЗ

Пусть испытываются n однотипных элементов (говорят, что рассматривается выборка объема n) для проверки каких-либо предположений об их надежности (например, предположение о показательности времени безотказной работы обычно нуждается в проверке). Поскольку статистический эксперимент носит вероятностный характер, при принятии решения можно ошибиться. Последствия ошибок могут быть неравнозначны: например, если нулевая гипотеза состоит в том, что некоторый элемент устройства неисправен и нуждается в замене, а альтернатива – в том, что элемент исправен, то ошибка второго рода может привести к финансовым потерям, а ошибка первого рода (то, что неисправный элемент не заменен) – к катастрофе. Обозна-

чим основную гипотезу H0, а альтернативную – H1. Нижеследующая табли-

ца дает представление о возможных ошибках.

Ошибки первого рода также называют ложноотрицательными решениями, а ошибки второго рода – ложноположительными. Эта терминология используется, в частности в медицинской литературе.

Нельзя уменьшать одновременно вероятности ошибок первого рода и второго рода: стремясь к уменьшению одной, обычно увеличивают другую. Статистические критерии строятся таким образом, чтобы вероятность ошибки первого рода была ограничена сверху какой-либо маленькой величиной α (число α называется уровнем значимости). Обычно выбирают стандартные значения уровня значимости: 0,1; 0,05; 0,01 и т. д. Для проверки гипотезы вычисляют функцию от выборочных данных, которая называется статистикой критерия. Если значение этой функции выходит за пределы критических значений, то нулевая гипотеза отвергается; если нет, то говорится, что данные не противоречат нулевой гипотезе на уровне α. Критические значения для известных критериев можно найти в статистических таблицах.

Если обозначить вероятность ошибки второго рода через β, то число

1 − β называется мощностью критерия. Мощность может зависеть от альтер-

нативы. При фиксированном уровне значимости мощность критерия увеличивается с увеличением объема выборки и должна стремиться к единице, ко-

17

гда объем выборки стремится к бесконечности – это свойство называется со-

стоятельностью критерия.

Критическое значение уровня α – это такое число ξα, что при нулевой гипотезе вероятность того, что статистика критерия превзойдет ξα, меньше или равна α.

Пример. Пусть эксперимент состоит в подбрасывании монеты, а его возможные исходы – 0 и 1 (орел и решка). Пусть нулевая гипотеза состоит в том, что вероятности выпадения 0 и 1 равны (т. е. монета симметрична), а альтернатива – в том, что они различны. Можно также рассматривать одностороннюю альтернативу: вероятность выпадения 0 больше, чем 1 (или наоборот). Предположим, что после 10 бросаний выпали девять орлов и одна решка. Найдем следующие вероятности:

1) вероятность того, что выпадет не менее девяти орлов:

2) вероятность того, что выпадет не менее девяти орлов или не более одного орла, равна удвоенной вероятности из первого пункта.

Так как обе эти вероятности не превосходят 0,05, можно утверждать, что данные противоречат нулевой гипотезе на уровне 0,05. Таким образом, при проверке нулевой гипотезы как против односторонней, так и против двусторонней альтернатив нужно отвергнуть нулевую гипотезу.

Статистические гипотезы делятся на параметрические (гипотезы о параметре распределения из известного семейства) и непараметрические – гипотезы о виде распределения. Так, гипотеза из ранее приведенного примера – это параметрическая гипотеза о параметре биномиального распределения. В качестве примера непараметрической гипотезы можно привести гипотезу

симметрии: для любого x выполняется равенство P( X > x) = 1 − P( X ≤ x), где

X – это интересующая нас случайная величина.

Следующий раздел также посвящен проверке непараметрической гипотезы, которая состоит в том, что две выборки взяты из одного и того же (неизвестного) распределения.

Более подробно о проверке гипотез можно прочесть, например в учебном пособии [7]. В [1] этой теме также уделяется несколько разделов.

11. РАНГОВЫЙ КРИТЕРИЙ ВИЛКОКСОНА

18

Задача 13. Пусть шесть рабочих работают по плану А, а восемь рабочих – по плану В. Проверим гипотезу о том, что производительность труда зависит от плана работы. Далее приведено количество часов, которое затратил на выполнение работы каждый из рабочих.

Гипотеза H0 состоит в том, что производительность труда не зависит от плана. Применим ранговый критерий Вилкоксона. Для этого объединим выборки в одну, упорядоченную по возрастанию. Найдем для выборки A и для выборки B суммы рангов, т. е. мест, которые они занимают в объединенной выборке:

Для удобства данные, относящиеся к плану А, выделены жирным шриф-

том. Суммы рангов TA и TB равны, соответственно,

TA = 1 + 2 + 3 + 6 + 11 + 12 = 35,

14

TB = 4 + 5 + 7 + 8 + 9 + 10 + 13 + 14 = ∑ k − TA = 70. k =1

Сумма величин TA и TB зависит только от суммы объемов выборок m + n, поскольку равна сумме всех чисел от 1 до m + n (в данном случае m + n = 14 и TA + TB = 105 ). Вторая величина может служить для контроля правильности вычислений. Обычно вычисляют суммы рангов для выборки меньшего объема. Сравним TA с верхним и с нижним критическими значе-

ниями. Таблицы для критерия Вилкоксона можно найти, например в [1].

В литературе можно встретить эквивалентный критерий U, и таблицы строятся обычно именно для него. Для вычисления этого критерия находят число инверсий, т. е. таких пар ( xi , y j ), что xi < y j , где xi – элементы пер-

вой выборки, а y j – второй. Интуитивно ясно, что при одинаковых законах распределения количество таких пар составляет примерно половину от обще-

го числа пар ( xi , y j ). Выполняется соотношение (проверьте!)

U = mn + m(m + 1)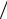2 − TA.

19

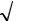
В рассматриваемом случае U = 6 ×8 + 6 × (6 +1)2 - 35 = 34. Из сумм ран-

гов видно, что данные не противоречат нулевой гипотезе, т. е. планы A и B не отличаются.

При m, n ³10 статистика

имеет приближенно стандартное нормальное распределение.

12. ПРОВЕРКА ГИПОТЕЗЫ О ПРИНАДЛЕЖНОСТИ ПОКАЗАТЕЛЬНОМУ ЗАКОНУ

Задача 14. Пусть времена безотказной работы набора из десяти однотипных устройств принимают следующие значения:

Гипотеза H0 состоит в том, что данная выборка взята из показательного распределения. Требуется проверить эту гипотезу на уровне 0,95 против альтернативы: выборка взята из некоторого ВФИ-распределения.

Подчеркнем, что в данном случае точное распределение при нулевой гипотезе неизвестно. Для проверки показательности (или экспоненциальности) существует огромное количество тестовых статистик (см., например, обзор в [8]). Воспользуемся одним из самых простых для вычисления критериев, который с высокой эффективностью проверяет экспоненциальность против ВФИ-альтернатив, – критерием Джини.

Прежде всего вычислим среднее значение выборки: M = 3, 24. Далее нормируем элементы выборки, т. е. разделим их на М (это стандартная практика, когда параметр масштаба неизвестен). Наконец, отсортируем полученные числа по возрастанию, т. е. составим вариационный ряд:

0,33; 0,39; 0,60; 0,65; 0,73; 0,98; 1,45; 1,50; 1,61; 1,72.

Односторонняя статистика Джини выглядит так:

n

∑ (n −1 − 2k )Y(k )

20