
Sb99044
.pdfМИНОБРНАУКИ РОССИИ
––––––––––––––––––––––––––––––––––––––––––––––––––––
Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В. И. Ульянова (Ленина)
–––––––––––––––––––––––––––––––––––––––––––
ПРАКТИКУМ ПО МЕТРОЛОГИИ
Учебное пособие
Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»
2020
1
УДК 621.37(075.8) (07)
ББК Ж 10я7
П54
Авторы: Е. М. Антонюк, П. Е. Антонюк, Е. Г. Бишард, Н. В. Орлова,
В. В. Поливанов.
П54 Практикум по метрологии: учеб. пособие к практическим занятиям / под ред. Е. М. Антонюка. СПб.: Изд-во СПбГЭТУ «ЛЭТИ», 2020. 32 с.
ISBN 978-5-7629-2631-7
Содержит краткие теоретические сведения по нормированию основной погрешности средств измерений и методикам обработки и представлению результатов измерений, задачи для проведения практических занятий, а также вопросы для самоконтроля, позволяющие оценивать результаты изучения дисциплины «Метрология» в течение семестра.
Предназначено для студентов СПбГЭТУ «ЛЭТИ» всех специальностей.
УДК 621.37(075.8) (07)
ББК Ж 10я7
Рецензенты: кафедра прикладной математики и информатики Высшей школы технологии и энергетики Санкт-Петербургского государственного университета промышленных технологий и дизайна (СПбГУПТД); д-р техн. наук, проф. В. Д. Мазин (Высшая школа киберфизических систем и управления Санкт-Петербургского политехнического университета Петра Великого).
Утверждено редакционно-издательским советом университета
в качестве учебного пособия
ISBN 978-5-7629-2631-7 |
© СПбГЭТУ «ЛЭТИ», 2020 |
|
2 |
Введение
Пособие предназначено для проведения практических занятий по дисциплине «Метрология».
Пособие включает методические материалы к практическим занятиям по дисциплине, содержащие краткие теоретические сведения по важнейшим разделам и задачи. Тематика задач направлена на закрепление знаний и приобретение умения и навыков, необходимых:
−при обработке и представлении результатов измерений по стандартным методикам;
−по применению метрологических характеристик для оценки погрешности результатов измерений;
−при представлении результатов измерений.
В пособии рассматриваются способы нормирования метрологических характеристик средств измерений (СИ) и их применение для оценки погрешности измерения, стандартные методики обработки и представления результатов для важнейших видов измерений:
−прямых;
−косвенных;
−многократных прямых.
1.ОЦЕНКА ОСНОВНОЙ ПОГРЕШНОСТИ СРЕДСТВ ИЗМЕРЕНИЙ
1.1. Нормирование основной погрешности средств измерений
Погрешностью измерения называют отклонение результата измерения от истинного значения измеряемой величины. Поскольку истинное значение остается неизвестным, погрешность оценивают, заменяя истинное значение действительным значением измеряемой величины, т. е. значением, определяемым опытным путем с помощью других, более точных средств измерений.
Погрешности выражаются в виде абсолютной, относительной и приведенной погрешностей.
Абсолютная погрешность – разность между результатом измерения X и истинным (действительным) значением измеряемой величины X0, т. е.
= X − X0 . |
(1.1) |
Относительная погрешность – отношение абсолютной погрешности к значению измеряемой величины (обычно в процентах)
δ = |
|
100 . |
(1.2) |
X |
|||
3 |
|
|
|
Приведенная погрешность – отношение абсолютной погрешности к нормирующему значению
γ = |
|
100 . |
(1.3) |
X N |
Для оценки погрешности результатов измерения используется определенная метрологическая характеристика СИ – его класс точности [1].
Класс точности СИ – обобщенная характеристика данного типа СИ, отражающая уровень точности, выражаемая пределами допускаемых основной и дополнительной погрешностей, а также другими характеристиками, влияющими на точность, значения которых устанавливаются в стандартах на отдельные виды средств измерений.
Возможны три варианта задания класса точности в зависимости от характера изменения основной абсолютной погрешности по диапазону измерения.
Для СИ с неизменяющейся абсолютной погрешностью по диапазону измерения (аддитивная погрешность) класс точности устанавливает предел до-
пускаемой приведенной основной погрешности γ [%] в виде числа, удовлетво-
ряющего выражению (1.3). В этом случае класс точности прибора обозначают
одним числом, выбираемым из ряда (1,0; 1,5; 2,5; 4,0; 5,0; 6,0)10n, где n = 1; 0; –1; –2; … .
Нормирующее значение XN в (1.3) выбирается в зависимости от пределов измерения СИ и равно:
1)большему из пределов измерений, если нулевая отметка расположена на краю или вне диапазона измерения;
2)сумме модулей пределов измерения, если нулевая отметка расположена внутри диапазона измерения;
3)длине шкалы или ее части, соответствующей диапазону измерения, если шкала существенно неравномерна, например у омметра;
4)номинальному значению измеряемой величины, если таковое установлено (например, у частотомера с номинальным значением 50 Гц);
5)модулю разности пределов измерений, если принята шкала с условным нулем (например, для температуры), и т. д.
Для СИ с линейно изменяющейся абсолютной погрешностью по диапазону измерения (мультипликативная погрешность) = bX класс точности устанавливает пределы допускаемой основной относительной погрешности
4
δ [%] в виде числа, удовлетворяющего выражению (1.2). Класс точности в этом случае обозначают числом, помещенным в кружок.
Для СИ с аддитивно-мультипликативным характером изменения основной абсолютной погрешности ее пределы задаются в виде суммы аддитивной и мультипликативной составляющих:
= ± (a + bX ) , |
(1.4) |
где а – постоянная величина; b – постоянное число; X – значение измеряемой величины. При этом класс точности может быть указан в виде двух чисел с/d, входящих в соотношение, которое является оценкой пределов допускаемой основной относительной погрешности [%]:
|
|
|
|
XК |
|
|
|
|
|
|
|
|
|
|
|||||||
δ = ± c + d |
|
|
|
|
|
− 1 |
, |
(1.5) |
||
X |
||||||||||
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|||||||
где XК – больший (по модулю) из пределов измерений СИ.
Значения с/d в обозначении класса точности также выбираются из ряда чисел, приведенного ранее, причем с > d.
Зная класс точности СИ, можно из (1.1)–(1.5) оценить пределы основной абсолютной погрешности ± для конкретного результата измерения. Значение измеряемой физической величины X0 находится в интервале
X = X0 ± , |
(1.6) |
где X0 – результат измерения; ± – пределы допускаемой основной абсо-
лютной погрешности.
Правила записи результата измерения в соответствии с (1.6) будут рассмотрены далее.
1.2. Определение погрешностей косвенных измерений
Косвенные измерения – это измерения, при которых искомое значение результатов измерений находят на основании прямых измерений других величин, функционально связанных с искомой величиной:
y = F(X1, X2, ..., Xm) ,
где y – искомое значение величины; X1, X2, ..., Xm – значения величин, полу-
ченных с помощью прямых измерений, которые по аналогии с математикой называют аргументами.
Особенностью косвенных измерений является одновременное измерение аргументов, что позволяет получить значение измеряемой величины, соответствующее моменту времени измерения аргументов. При измерении значе-
5
ний аргументов результат всегда получают с некоторой погрешностью, которая в общем случае состоит из систематической и случайной составляющих. Результат косвенных измерений получают при подстановке в приведенное уравнение оценок аргументов.
Для нахождения границ абсолютной погрешности результата косвенных измерений воспользуемся формулой полного дифференциала, заменив дифференциал на приращение, т. е. на абсолютную погрешность:
y = |
∂F |
x + |
∂F |
x |
+ ... + |
∂F |
x , |
|
|
|
|||||
|
1 |
2 |
|
∂xm |
m |
||
|
∂x1 |
∂x2 |
|
|
|||
где ∂F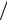 ∂xi – частная производная от функции y по одному из аргументов; x1, x2, ..., xm – абсолютные погрешности измерения аргументов.
∂xi – частная производная от функции y по одному из аргументов; x1, x2, ..., xm – абсолютные погрешности измерения аргументов.
Функция |
Абсолютная погрешность |
Относительная погрешность, % |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||
y = x1 + x2 |
y = ± ( |
x1 + |
x2 ) |
y = ± |
100( |
x1 + |
x2 ) |
|||||||||
|
|
|
|
|
|
|
|
|
x1 + x2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = x1 − x2 |
y = ± ( |
x1 + |
x2 ) |
y = ± |
100( |
x1 + |
x2 ) |
|||||||||
|
|
|
|
|
|
|
|
|
x1 − x2 |
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
y = x1x2 |
y = ± (x1 x1 + x2 x2 ) |
|
|
|
|
x |
x |
|
||||||||
|
|
|
|
|
|
y = ±100 |
|
|
1 |
+ |
|
2 |
|
|||
|
|
|
|
|
|
|
x |
|
x |
|||||||
|
|
|
|
|
|
|
|
|
|
1 |
|
|
2 |
|
||
y = x1 x2 |
y = ± |
x1 x1 + x2 x2 |
|
|
|
|
x |
x |
|
|||||||
|
|
|
|
|
y = ±100 |
|
|
1 |
+ |
|
2 |
|
||||
|
|
x2 |
|
|
||||||||||||
|
|
|
|
|
x |
|
x |
|||||||||
|
|
|
2 |
|
|
|
|
|
|
1 |
|
|
2 |
|
||
В таблице представлены формулы для определения абсолютных и относительных погрешностей для часто встречающихся случаев косвенных измерений с двумя аргументами.
1.3. Обработка результатов измерений. Многократные измерения
Целью обработки результатов измерений (наблюдений) является установление значения измеряемой величины и оценка погрешности полученного результата измерения. Методы обработки результатов наблюдений могут быть разными в зависимости от предварительной информации, которой располагает экспериментатор об источниках и характере проявления погрешностей, условиях эксперимента, свойствах используемых средств измерений, от вида измерений, числа выполненных наблюдений и других причин [2].
Погрешность измерения проявляет себя как случайная величина. Следовательно, и результаты отдельных измерений одного и того же значения измеряемой величины случайны. Если систематическая погрешность при измерении этой величины постоянна, что является весьма распространенным слу-
6
чаем на практике, то вид закона распределения отдельных результатов измерения определяется видом закона распределения случайных погрешностей. При этом математическое ожидание этого закона распределения смещено с истинного значения измеряемой величины на систематическую погрешность, а дисперсия этого закона распределения равна дисперсии случайной составляющей погрешности. Отсюда следует, что для получения оценки измеряемой величины, максимально близкой к исходному значению, необходимо по экспериментальным данным найти оценку математического ожидания отдельных результатов наблюдений, оценить систематическую погрешность и исключить ее из оценки математического ожидания. В общем случае, когда отдельные результаты измерений содержат различные систематические погрешности, необходимо оценить каждую из погрешностей, исключив ее из соответствующего результата измерения и, получив, таким образом, ряд наблюдений, не содержащий систематических погрешностей, оценить математическое ожидание.
Точность оценки математического ожидания ряда наблюдений зависит от количества выполняемых измерений и дисперсии случайной составляющей погрешности. Поэтому по экспериментальным данным приходится оценивать не только математическое ожидание, но и дисперсию.
Рассмотрим наиболее характерные случаи обработки результатов наблюдений.
Предположим, что при многократном измерении интересующей нас величины получили n отдельных результатов наблюдений. Исключив систематическую погрешность из каждого наблюдения, получаем исправленный ряд значений x1, x2, ..., xn , математическим ожиданием которого является дей-
ствительное значение измеряемой величины. За действительное значение измеряемой величины принимаем среднее арифметическое
|
|
|
|
n |
|
|
x1 + x2 + ... + xn |
|
xi |
||
x = |
= |
i=1 |
. |
||
|
|
||||
|
n |
|
|
n |
|
Отклонения между отдельными |
значениями наблюдений и средним |
||||
арифметическим (разности ρ1 = x1 − x; ρ2 = x2 − x; ...; ρn = xn − x ) называют-
ся случайными отклонениями результатов наблюдений (или остаточными погрешностями). Они могут быть как положительными, так и отрицательными. На основании свойства среднего арифметического алгебраическая сумма
7

n
остаточных погрешностей равна нулю, т. е. ρi = 0; этим следует пользо- i=1
ваться для контроля правильности подсчета x .
Если дисперсия σ2 полученного ряда наблюдений известна из предыдущих экспериментов или из технической документации на применяемые средства измерений, то дисперсию среднего арифметического можно опреде-
лить по формуле σ2[x ] = σ2[x] , где σ2[x] − дисперсия исправленного ряда n
наблюдений; σ2[x] − дисперсия действительного значения (среднего арифметического) измеряемой величины этого ряда.
Если дисперсия ряда неизвестна, то ее оценку можно найти по формуле
|
n |
|
|
|
S2[x] = |
ρi2 |
|
|
|
i=1 |
, |
(1.7) |
||
n − 1 |
||||
|
|
|
где ρi – остаточные погрешности исправленного ряда наблюдений. В этом случае за оценку дисперсии действительного значения измеряемой величины нужно принять
S2[x] = S2[x] / n. |
(1.8) |
Для нахождения доверительного интервала погрешности измерения |
|
необходимо найти закон распределения для величины |
|
(x − xи) / σ[x] |
(1.9) |
при известной дисперсии или для величины |
|
(x − xи) / S[x] |
(1.10) |
при неизвестной дисперсии. |
|
Так как в (1.9) входит только одна случайная величина x , то вид закона распределения величины, определяемой этим выражением, определяется видом закона распределения величины x . При нормальном законе распределения отдельных результатов xi закон распределения x тоже нормальный. Это
объясняется известным из теории вероятностей свойством устойчивости нормального закона, заключающимся в том, что сумма случайных величин, распределенных по нормальному закону, дает случайную величину, распределенную по нормальному закону. Таким образом, при нормальном законе
8

распределения xi случайная величина, определяемая (1.9), имеет нормальный
закон распределения с математическим ожиданием, равным нулю, и дисперсией, равной единице. Случайную величину с таким нормальным законом распределения обозначим z .
Выражение (1.10) содержит две случайные величины x и S[x ] , поэтому закон распределения величины, определяемой (1.10), отличается от закона распределения величины, определяемой (1.9). В теории вероятностей доказано, что при нормальном законе распределения xi случайная величина, опре-
деляемая (1.10), имеет закон распределения Стьюдента. Случайную величину, распределенную по закону Стьюдента, обозначим t . Для z и t существуют таблицы, по которым можно найти значения zP и tP ( f ) , определяющие с доверительной вероятностью P границы доверительного интервала для величин z и t соответственно. Число f называется числом степеней свободы; для рассмотренного случая f = n − 1.
Чем больше число измерений в ряду наблюдений, тем ближе оценка S[x] совпадает со средним квадратическим отклонением σ[x ] . Следовательно, с увеличением числа наблюдений закон распределения Стьюдента приближается к нормальному закону. Практически при n >30 zP
Зная zP или tP ( f ) , на основании (1.9) и (1.10) с учетом (1.7) и (1.8) результат измерения с доверительной вероятностью P можно записать в виде
x = x ± z |
P |
σ[x] = x ± z |
P |
σ[x] |
(1.11) |
|||||
и |
|
|
|
n |
|
|||||
|
|
|
|
|
|
|
|
|||
при известной дисперсии или в виде |
|
|
|
|
|
|
||||
x |
= x ± t |
P |
( f )S[x] = x ± t |
P |
( f ) |
S[x] |
|
(1.12) |
||
|
||||||||||
и |
|
|
|
|
|
n |
|
|||
|
|
|
|
|
|
|
|
|
||
при неизвестной дисперсии.
Если закон распределения отдельных результатов измерения xi отлича-
ется от нормального, то найти закон распределения случайных величин, определяемых (1.9) и (1.10), затруднительно. В этом случае могут быть даны следующие рекомендации. Вид закона распределения x определяется законом распределения суммы независимых случайных величин xi , среди кото-
рых нет преобладающих (все xi имеют один и тот же закон распределения).
На основании центральной предельной теоремы закон распределения x с увеличением числа наблюдений стремится к нормальному закону. Практически при n > 5 можно считать, что закон распределения x близок к нормаль- 9
ному закону и при известном σ[x] для приближенной оценки доверительного
интервала можно пользоваться (1.11). Если дисперсия σ2 [x] неизвестна, то необходимо увеличить число наблюдений n , так чтобы оценка S[x] была близка к σ[x] . Практически это условие выполняется при n > 30. В этом случае для приближенной оценки доверительного интервала можно также пользоваться (1.11).
На практике часто встречается однократное измерение, когда измеряемая величина оценивается по результату одного наблюдения. Этот случай можно рассматривать как частный случай многократных измерений (при n = 1). То-
гда (1.11) и (1.12) примут вид |
|
xи = x ± zPσ; |
(1.13) |
xи = x ± tP (f )S. |
(1.14) |
Здесь за действительное значение x измеряемой величины следует принять результат однократного измерения, из которого исключена систематическая погрешность. Нужно иметь в виду, что по однократному измерению нельзя определить σ (или S ). Поэтому для того чтобы можно было записать результат измерения в виде (1.13), среднее квадратическое отклонение σ нужно знать на основании предварительных измерений или из технической документации на применяемое средство измерений. Если вместо σ известна его оценка S , найденная по некоторому числу предварительных измерений, то для определения tP (f ) в (1.14) число степеней свободы f нужно взять равным
этому числу предварительных измерений минус единица.
1.4. Представление результатов измерений
Выражение (1.6) является оценкой интервала, в котором находится значение измеряемой величины. При вычислении получаемые значения могут содержать большое число цифр, что создает впечатление о высокой точности измерений. Возникает задача округления значений абсолютной погрешности до определенного числа значащих цифр, которые являются достоверными.
Определим понятие значащих цифр, которыми при записи приближенного числа после округления считаются:
−все ненулевые цифры;
−нули, содержащиеся между ненулевыми цифрами;
−нули, являющиеся представителями сохраненных десятичных разрядов при округлении.
10
