
LS-Sb87070
.pdf
3. Условие перпендикулярности прямой и плоскости имеет вид
A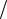 l B
l B m C
m C n .
n .
Оно равносильно условию коллинеарности векторов N и s (N || s) .
4. Условие принадлежности прямой L плоскости P записывается в виде
Al Bm Cn 0, |
(L || P), |
(3.2) |
|||||||
Ax |
By |
Cz |
0 |
D 0, |
(M |
0 |
P), |
||
|
0 |
0 |
|
|
|
|
|
||
где x0, y0, z0 координаты точки M0 , принадлежащей прямой.
|
|
|
|
|
|
3.2. Решение типовых задач |
|
|
|
|
|
|
|
|
|
|||||||||||||
Задача 3.1. Найти острый угол между прямой |
x 3 |
|
|
y 6 |
|
z 7 |
и |
|||||||||||||||||||||
|
|
|
||||||||||||||||||||||||||
плоскостью 4x 2 y 2z 3 0 . |
|
|
|
|
|
|
|
|
|
1 |
|
1 |
|
2 |
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Направляющий вектор прямой равен s(1, 1, 2) . Нормальный |
||||||||||||||||||||||||||||
вектор плоскости равен N |
(4, 2, 2) . По формуле (3.1) |
|
|
|
|
|
|
|||||||||||||||||||||
sin |
|
|
|
Al Bm Cn |
|
|
|
|
|
|
|
|
4 1 2 1 2 ( 2) |
|
1 , |
. |
||||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
2 |
|
2 |
|
2 |
|
2 |
|
|
2 |
|
|
2 |
|
1 1 4 |
16 4 4 |
|
|||||||||||
|
|
|
C |
l |
m |
n |
|
|
2 |
|
6 |
|
||||||||||||||||
|
A B |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: 6. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
Задача 3.2. При каком значении C прямая L : |
3x 2 y z 3 0, |
парал- |
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4x 3y 4z 1 0 |
|
|
|||||||
лельна плоскости |
P : 2x y Cz 2 0 ? |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
Решение. Согласно условию задачи прямая L задана как линия пересечения |
||||||||||||||||||||||||||||
двух плоскостей. |
Нормальный |
вектор |
первой плоскости равен N1(3, 2, 1) , |
|||||||||||||||||||||||||
нормальный вектор второй плоскости равен N2 (4, 3, |
4) . Направляющий век- |
|||||||||||||||||||||||||||
торпрямойравен s N |
N |
|
(см. формулу(2.6)): |
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
1 |
2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
|
s |
|
|
i |
|
j |
|
5i 8 j k . |
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
3 |
2 |
1 |
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
4 |
3 |
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
|
|
|
||||||||||||||||||||||||
Условие параллельности прямой L и плоскости P |
|
это условие ортогональ- |
||||||||||||||||||||||||||
ности направляющего вектора прямой |
s( 5, 8, 1) |
и нормального вектора |
||||||||||||||||||||||||||
плоскости N |
(2, 1, C) , т. е. N s 0 . Умножая, получаем |
|
|
|
|
|
|
|||||||||||||||||||||
2 ( 5) ( 1) ( 8) C( 1) 0 C 2 .
21
Таким образом, уравнение плоскости будет 2x y 2z 2 0.
Ответ: C 2. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.3. При каких значениях C и D прямая |
x 3 |
|
y 3 |
|
z |
лежит |
|||||||||||
|
|
3 |
|
||||||||||||||
|
|
|
|
2 |
|
|
|
|
7 |
|
|
||||||
в плоскости 2x y Cz D 0 ? |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Прямая будет параллельна плоскости, если ее направляю- |
|||||||||||||||||
щий вектор s(2, 3, |
7) будет ортогонален нормальному вектору плоско- |
||||||||||||||||
сти N (2, 1, |
C) , т. е. N s 0 . Запишем это условие: |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
2 2 1 ( 3) 7C 0 C 1. |
|
|
|
|
|
|
|
|
|
|
|
||||
Прямая |
будет |
принадлежать |
плоскости, |
если |
координаты |
точки |
|||||||||||
M0 (3, 3, 0) , через которую проходит прямая, удовлетворяют уравнению |
|||||||||||||||||
плоскости: M0 P . Отсюда получаем, что |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
2 3 3 1 0 D 0 D 3. |
|
|
|
|
|
|
|
|
|
|
|
||||
При решении задачи мы воспользовались формулой (3.2). |
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: C 1, |
D 3. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Задача 3.4. Найти точку пересечения прямой |
L : |
x 6 |
|
y 5 |
|
|
z 6 |
и |
|||||||||
|
|
|
|||||||||||||||
|
|
|
|
1 |
3 |
|
|
|
4 |
||||||||
плоскости P : x 3y 4z 7 0. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Запишем уравнения прямой в параметрическом виде |
|
|
|||||||||||||||
|
|
x 6 t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
5 3t, |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
y |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
z 6 4t. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Подставляя выражения для x, y, z в уравнение плоскости P , получим |
|
|
|||||||||||||||
6 t1 15 9t1 24 16t1 7 0 26t1 52 t1 2. |
|
|
|||||||||||||||
Теперь следует подставить значение параметра |
t1 2 |
в параметрические |
|||||||||||||||
уравнения прямой L . Находим x1 4, y1 1, z1 2 . |
|
|
|
|
|
|
|
|
|
|
|
||||||
Ответ: M1(4, 1, 2). |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полезная формула. Если прямая L : x x0 |
lt, y y0 mt, |
z z0 nt |
|||||||||||||||
пересекается с плоскостью P : Ax By Cz D 0 , то точке пересечения M1 отвечает значение параметра
t |
Ax0 By0 Cz0 D |
. |
(3.3) |
|
|||
1 |
Al Bm Cn |
|
|
|
|
||
22

Задача 3.5. Найти уравнение плоскости P1,
L : x 6 y 1 z 4 перпендикулярно плоскости
2 1 1
Решение. Плоскость P1 имеет два направляющих вектора s(2, 1, 1) и N2(1, 1, 1) и проходит через точку M0 (6, 1, 4) (рис. 3.1). Согласноформуле(1.9) ееуравнениебудетиметьвид
проходящей через прямую
P2 : x y z 1 0.
P2
N2
|
x 6 |
y 1 |
z 4 |
|
0, |
M0 |
L |
|
|
||||||
|
2 |
1 |
1 |
|
|||
|
|
s |
|||||
|
1 |
1 |
1 |
|
|
|
|
или |
|
|
|
|
P |
|
|
|
|
|
|
1 |
|
||
2(x 6) 3( y 1) (z 4) 0 . |
Рис. 3.1 |
|
Окончательно: 2x 3y z 5 0 .
Ответ: 2x 3y z 5 0 .
Задача 3.6. Известны координаты вершин тетраэдра: A1(3, 2, 3); A2(0, 1, 2); A3(5, 5, 4); A4 (4, 3, 5). Найтиуравнениеидлинуеговысоты A4 A5 .
Решение. Данный тетраэдр мы рассматривали в |
|
|
|
||||||
задаче 1.10. Уравнение основания A A A |
имеет вид |
|
A4 |
|
|||||
|
|
1 |
2 |
3 |
|
|
|
|
|
2x y 7z 13 0 . В качестве направляющего век- |
|
h |
A3 |
||||||
тора s |
высоты A4 A5 можно выбрать нормальный |
|
|
||||||
|
|
|
|||||||
|
|
|
|
|
|
|
A1 |
A5 |
|
вектор грани |
A1A2 A3 , т. е. s N (2, 1, |
7) |
(рис. 3.2). |
|
|
A2 |
|||
Кроме |
того, |
нам известны координаты |
точки |
|
Рис. 3.2 |
|
|||
A4 (4, 3, 5) , через которую проходит |
|
высота. |
Вос- |
|
|
|
|||
пользуемся каноническими уравнениями прямой (2.3). Тогда получим |
|
||||||||
A4 A5 : x 4 y 3 z 5 . 2 1 7
Высоту h можно найти по формуле (1.5), определяющей расстояние от точки
A4 (4, 3, 5) до грани A1A2 A3 : 2x y 7z |
13 0 . |
|
|
|||||||||||
h |
|
|
Ax4 By4 Cz4 D |
|
|
| 2 |
4 1 3 7 5 13| |
|
11 6 . |
|||||
|
|
|
||||||||||||
|
|
|||||||||||||
|
|
|
A |
2 |
B |
2 |
C |
2 |
|
|
|
54 |
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|||
23

(Напомним, что A, B, |
C, |
D – это коэффициенты в общем уравнении плоско- |
||||||||||||||||||||||||||||||||||||||||
сти 2x y 7z 13 0 , и они равны A 2 , B 1, C 7 , D 13.) |
|
|
|
|
||||||||||||||||||||||||||||||||||||||
Ответ: A A |
: |
|
x 4 |
|
y 3 |
|
z 5 |
; |
h 11 6 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
4 |
5 |
|
|
2 |
|
|
1 |
|
|
7 |
|
|
18 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
Задача 3.7. Даны прямые L : |
|
x 6 |
|
y 1 |
|
|
z 4 |
|
и L |
: |
|
|
x 1 |
|
|
y 2 |
|
z 7 |
. |
|||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
2 |
1 |
|
|
|
1 |
|
2 |
1 |
|
|
|
1 |
|
|
7 |
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
Найти уравнение плоскости P, проходящей через прямую L1 параллельно |
||||||||||||||||||||||||||||||||||||||||||
прямой L2. |
|
Векторы s1(2, 1, 1) |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
Решение. |
|
и |
s2 (1, 1, 7) являются направляющими |
|||||||||||||||||||||||||||||||||||||
векторами плоскости P (рис. 3.3). Точка M1(6, 1, 4) принадлежит плоскости P . |
||||||||||||||||||||||||||||||||||||||||||
Решаемзадачу, используяформулу(1.9): |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
x 6 |
|
y 1 |
z 4 |
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||
|
|
L2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
|
|
|
1 |
|
1 |
|
|
|
0, |
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
1 |
|
|
|
1 |
7 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
s1 |
|
|
|
|
|
|
|
|
|
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
|
|
|
|
|
L1 |
|
|
|
6(x 6) 15( y 1) 3(z 4) 0. |
|
|
|
|
|||||||||||||||||||||||||||||
|
|
|
|
|
|
P |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Окончательно: 2x |
5y z 11 0 . |
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
Рис. 3.3 |
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
Ответ: 2x 5y z 11 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
Задача 3.8. Составить уравнение плоскости, проходящей через прямую |
||||||||||||||||||||||||||||||||||||||||
L : |
x 1 |
|
y 1 |
|
|
z 2 |
|
|
и точку M1(3, 0, 2) . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
4 |
|
|
|
3 |
|
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
|
|
Решение. Прямая L проходит через точку M0( 1, 1, 2) и ее направля- |
||||||||||||||||||||||||||||||||||||||||
ющий вектор равен s(4, 3, 1) . Произвольная |
точка M (x, y, z) будет при- |
|||||||||||||||||||||||||||||||||||||||||
надлежать искомой плоскости P , если векторы |
|
|
и s |
компла- |
||||||||||||||||||||||||||||||||||||||
M0M , |
M0M1 |
|||||||||||||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
нарны: |
M0M |
M0M1 s 0 (рис. 3.4), т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
P |
|
|
|
L |
|
|
|
|
|
|
|
|
|
|
|
x x |
y y |
z z |
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
|
|
|
0 |
|
0 |
|
|
|
|
|
|
|
|
|
||||||||
|
|
M0 |
|
|
|
M1 |
|
|
|
|
|
|
|
x1 x0 |
y1 y0 |
z1 z0 |
|
0 . |
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
l |
|
|
m |
|
n |
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
M |
|
|
|
|
|
|
|
|
|
Это и есть уравнение плоскости P . |
Подставляем |
|||||||||||||||||||||||||||
|
|
|
Рис. 3.4 |
|
|
|
|
|
|
координаты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
24

x 1 |
y 1 |
z 2 |
|
|
|||
4 |
1 |
4 |
0, |
4 |
3 |
1 |
|
или
11(x 1) 12( y 1) 8(z 2) 0 .
Окончательно: 11x 12 y 8z 17 0 .
Ответ: 11x 12 y 8z 17 0 .
Полезная формула. Уравнение плоскости, проходящей через прямую
L : |
x x0 |
|
y y0 |
|
|
z z0 |
и |
точку M |
1 |
(x , y , z ) , не лежащую на этой |
|||||
|
|
|
|
||||||||||||
|
l |
|
m |
|
n |
|
1 |
1 |
1 |
|
|||||
|
|
|
|
|
|
|
|
|
|
||||||
прямой, имеет вид |
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
x x0 |
y y0 |
z z0 |
|
|
|
|
||
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
x1 x0 |
y1 y0 |
z1 z0 |
|
0. |
(3.4) |
|||
|
|
|
|
|
|
|
|
l |
m |
|
n |
|
|
|
|
Задача3.9. Доказать, чтопрямые
|
|
L : |
x 1 |
|
|
y 2 |
|
z 3 |
; L |
|
: |
|
|
x 2 |
|
|
y 1 |
|
z 2 |
|
|
|
|
|
||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||||||
|
|
1 |
|
1 |
|
|
2 |
|
|
|
|
4 |
|
2 |
3 |
|
|
|
|
2 |
|
|
4 |
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
лежат в одной плоскости и найти уравнение этой плоскости. |
|
|
|
|
||||||||||||||||||||||||||||||
|
Решение. Первая прямая проходит через |
|
|
|
|
|
s2 |
L 2 |
|
|
|
|
||||||||||||||||||||||
точку M1(1, 2, 3) и ее направляющий век- |
|
|
|
|
|
|
|
|
|
|||||||||||||||||||||||||
|
|
|
|
|
M2 |
|
|
|
||||||||||||||||||||||||||
тор |
s1(1, 2, 4) . |
Вторая прямая проходит че- |
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||||
|
|
|
|
|
|
|
M 1 L |
|
|
|
||||||||||||||||||||||||
рез |
точку M 2 |
( 2, 1, 2) |
и |
|
ее |
направляю- |
|
|
|
|
|
|
|
s1 |
|
1 |
||||||||||||||||||
щим вектором является |
|
(3, 2, 4) . |
|
|
Оче- |
|
|
|
|
|
|
|
Рис. 3.5 |
|
|
|
||||||||||||||||||
s2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
видно, что прямые лежат в одной плоскости, если векторы |
, |
|||||||||||||||||||||||||||||||||
M1M2 |
|
|||||||||||||||||||||||||||||||||
|
|
|
s1 s2 0 (рис. 3.5), т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
компланарны: |
M1M2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
|
|
|
|
|
|
x2 x1 |
y2 y1 |
|
|
|
z 2 z1 |
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
l1 |
|
|
|
|
m1 |
|
|
|
|
|
n1 |
|
|
0 . |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
l2 |
|
|
|
|
m2 |
|
|
|
|
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||
Подставим заданные координаты: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
3 |
1 5 |
|
0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||
|
|
|
|
|
|
|
|
|
1 |
|
2 |
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
3 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
P
s1 и s2
25

Это означает, что прямые L1 и L2 лежат в одной плоскости. Векторы s1 и s2 не коллинеарны. Следовательно, эти прямые пересекаются.
Найдем уравнение плоскости |
P , |
в которой лежат прямые L1 и L2 . |
||||||||||
Очевидно, что произвольная точка M (x, |
y, z) |
будет принадлежать плоско- |
||||||||||
|
|
|
|
|
|
|
|
|
, s1, s2 компланарны: |
|||
s2 |
L2 |
P |
сти, если векторы M1M |
|||||||||
|
|
|
0 |
(рис. 3.6), т. е. |
||||||||
|
||||||||||||
|
M |
|
M1M |
s1 s2 |
||||||||
|
s1 M1 |
L1 |
|
|
|
x x1 |
y y1 |
z z1 |
|
0 . |
||
|
|
|
|
|
||||||||
|
Рис. 3.6 |
|
|
|
|
|
l1 |
m1 |
n1 |
|
||
|
|
|
|
|
|
l2 |
m2 |
n2 |
|
|
||
|
|
|
|
|
|
|
|
|
||||
Это и есть уравнение искомой плоскости. Подставляем координаты и вычисляем определитель разложением по элементам первой строки. Получаем
|
|
|
|
|
|
x 1 |
y 2 |
z 3 |
|
0 , |
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|||||||||||||||
|
|
|
|
|
|
1 |
|
2 |
|
4 |
|
|
|
|
|
|||||||||
|
|
|
|
|
|
3 |
|
2 |
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|||
или |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
16(x 1) 8( y 2) 8(z 3) 0 . |
|
|
|
||||||||||||||||||
Окончательно: 2x y z 3 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Ответ: 2x y z 3 0 . |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
Полезные формулы. Две прямые |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||
L : |
x x1 |
|
y y1 |
|
z z1 |
; L |
|
: |
x x2 |
|
y y2 |
|
z z2 |
|
||||||||||
|
|
|
|
|
|
|
||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
1 |
l1 |
|
m1 |
2 |
|
|
l2 |
|
m2 |
|
n2 |
|||||||||||||
|
|
n1 |
|
|
|
|
|
|||||||||||||||||
лежат в одной плоскости, если |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 x1 |
y2 y1 |
|
z 2 z1 |
|
|
|
|
|
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
l1 |
m1 |
|
|
n1 |
|
0. |
(3.5) |
||||||||||||
|
|
|
|
|
l2 |
m2 |
|
|
n2 |
|
|
|
|
|
|
|||||||||
Если прямые пересекаются, то уравнением этой плоскости будет |
||||||||||||||||||||||||
|
|
|
|
|
x x1 |
y y1 |
|
z z1 |
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
|
|
|
|
|
l1 |
m1 |
|
n1 |
|
|
|
|
0 . |
(3.6) |
|||||||||
|
|
|
|
|
|
l2 |
m2 |
|
n2 |
|
|
|
|
|
|
|
|
|
|
|
||||
Замечание. Прямые скрещиваются (т. е. не лежат в одной плоскости) то-
гда и только тогда, когда и равенство (3.5) несправедливо.
M1M2 s1 s2 0
26

Задача 3.10. Найти уравнение плоскости, проходящей через две парал-
лельные прямые: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
L : |
x 2 |
|
y 1 |
|
z 3 |
; |
L : |
x 1 |
|
|
y 2 |
|
z 3 |
. |
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|||||||||||||||
1 |
3 |
|
|
2 |
|
|
|
2 |
|
2 |
3 |
|
2 |
|
2 |
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||
Решение. Ясно, что направляющие векторы |
M2 |
|
P |
||||||||||||||||||||
этих прямых равны |
|
|
|
|
|
|
|
. Первая |
M |
||||||||||||||
s1 |
|
s2 |
s(3, 2, 2) |
s |
|
|
|||||||||||||||||
прямая проходит через точкуM1(2, 1, 3) , вто- |
|
|
M1 |
|
|
||||||||||||||||||
рая через точкуM2 (1, 2, 3) . Произвольная |
|
|
|
|
|||||||||||||||||||
Рис. 3.7 |
|
||||||||||||||||||||||
точка M (x, y, z) принадлежит искомой плоско- |
|
||||||||||||||||||||||
|
|
|
|||||||||||||||||||||
сти P , если векторы |
|
|
|
|
|
|
|
|
|
|
|
s 0 |
|||||||||||
M1M , |
|
M1M2 и s |
|
компланарны: |
M1M |
M1M2 |
|||||||||||||||||
(рис. 3.7), т. е. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x1 |
|
y y1 |
|
|
z z1 |
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
|
|
|
x2 x1 |
|
y2 y1 |
|
z2 z1 |
0 . |
|
|
|
|
|
|||||||||
|
|
|
|
|
l |
|
|
|
m |
|
|
|
n |
|
|
|
|
|
|
|
|
||
Подставляя заданные координаты, находим уравнение плоскости P :
x 2 |
y 1 |
z 3 |
|
0 , |
|
||||
1 |
3 |
6 |
|
|
3 |
2 |
2 |
|
|
или
6(x 2) 20( y 1) 11(z 3) 0 .
Окончательно: 6x 20 y 11z 1 0 .
Ответ: 6x 20 y 11z 1 0 .
Полезная формула. Уравнение плоскости, проходящей через две параллельные прямые ( L1 || L2 , s1 s2 s )
L : |
x x1 |
|
y y1 |
|
z z1 |
; L : |
x x2 |
|
y y2 |
|
z z2 |
, |
|||||
|
|
|
|
|
|
|
|||||||||||
1 |
l |
|
m |
n |
2 |
l |
|
|
m |
|
n |
||||||
|
|
|
|
|
|
|
|||||||||||
имеет вид |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
x x1 |
|
y y1 |
z z1 |
|
0 . |
(3.7) |
|||||||
|
|
|
|
|
|
||||||||||||
|
|
|
|
x2 x1 |
|
y2 y1 |
z2 z1 |
|
|||||||||
|
|
|
|
|
l |
|
|
m |
n |
|
|
|
|
|
|
||
Замечание. В задачах 1.3, 1.9, 3.5, 3.8–3.10 без труда можно указать два направляющих вектора искомых плоскостей. Поэтому решение этих задач
27

аналогично решению задачи 1.2. Если эти направляющие векторы явно не обозначены в ходе решения, то найдите их самостоятельно. Подумайте, что общего в формулах (1.7)–(1.9), (3.4)–(3.7).
Задача 3.11. |
Найти координаты |
проекции M1 точки M0 (1, |
2, 1) на |
||||
N |
|
M0 |
плоскость P : 3x y 2z 27 0 . |
|
|||
|
|
||||||
|
s |
Решение. Находим параметрические уравнения |
|||||
L |
|
|
прямой |
L , |
проходящей через точку M0 (1, 2, 1) |
||
|
|
перпендикулярно плоскости P . В качестве направ- |
|||||
|
|
M1 |
|||||
|
|
ляющего вектора s прямой L можно выбрать нор- |
|||||
P |
|||||||
|
мальный |
вектор N плоскости P , т. е. |
положить |
||||
Рис. 3.8 |
|
||||||
|
s N (3, 1, |
2) (рис. 3.8). Параметрические уравне- |
|||||
|
|
|
|||||
ния прямой L будут (см. формулу (2.2)): |
|
||||||
|
|
|
x 1 3t, |
|
|||
|
|
|
|
|
|
||
|
|
|
y 2 t, |
|
|||
|
|
|
|
1 2t. |
|
||
|
|
|
z |
|
|||
По формуле (3.3) находим значение параметра t t1, при котором прямая пересекает плоскость. Получим t1 2. Подставим это значение в параметрические уравнения прямой и вычислим координаты точки M1 :
|
|
x1 7, |
y1 0, |
z1 3. |
|
|
||
Ответ: M1(7, 0, 3). |
|
|
|
|
|
|||
Задача 3.12. Найти координаты точки M 2 , симметричной |
точке |
|||||||
M0 (1, 2, 1) |
относительно плоскости P : 3x y 2z 27 0 . |
|
||||||
M0 |
Решение. Воспользуемся результатом решения предыду- |
|||||||
щей задачи. Точка |
M1(7, 0, 3) – проекция точки M0 на |
|||||||
|
|
|||||||
|
|
плоскость. Координаты точки M2 (x2, y2, z2 ) можно найти, |
||||||
M1 |
используясоотношения: |
|
|
|
||||
(x0 x2) 2 x1, |
( y0 y2) 2 y1, |
(z0 z2) 2 z1 |
||||||
|
|
|||||||
M2 |
(рис. 3.9). Следовательно, |
|
|
|
||||
x2 2x1 x0 13, |
y2 2 y1 y0 2, |
z2 2z1 z0 |
7. |
|||||
Рис. 3.9 |
|
|||||||
|
Ответ: M 2 |
(13, |
2, |
7). |
|
|
||
|
|
|
|
|||||
28

Задача3.13. Найтикоординатыпроекции M1 точки M0 |
(0, |
2, 1) напрямую |
||||||
|
|
L : x 4 |
y 1 |
z 2 . |
|
|
|
|
|
|
2 |
1 |
3 |
|
|
|
|
Решение. Найдем уравнение плоскости P , перпен- |
|
|
|
|||||
дикулярной прямой |
L |
и проходящей |
через |
точку |
|
|
N |
|
M0 (0, 2, 1) . В качестве нормального вектора N плос- |
|
|
||||||
|
M0 |
|
||||||
кости P можно выбрать направляющий вектор |
s пря- |
|
s |
|||||
|
|
|||||||
мой L , т. е. положить N s(2, 1, |
3) (рис. 3.10). Тогда |
|
|
|||||
|
M1 |
L |
||||||
уравнение плоскости |
|
|
|
|
|
|
||
|
|
|
|
|
|
|
|
|
P : 2x ( y 2) 3(z 1) 0, |
|
|
|
P |
|
|||
или |
|
|
|
|
|
|
Рис. 3.10 |
|
2x y 3z 1 0.
Параметрические уравнения прямой L имеют вид
x 4 2t,y 1 t,
z 2 3t.
Далее решаем аналогично задаче 3.11. Координаты точки M1 находим с
помощью формулы (3.3). Получаем t1 1, |
x1 2, y1 0, z1 1. |
|
||||||||||||
Ответ: M1(2, 0, 1). |
|
|
|
|
|
|
|
|
|
|
||||
Задача 3.14. Найти координаты точки M 2 |
, симмет- |
M0 |
||||||||||||
ричной точке M0 (0, 2, 1) относительно прямой |
||||||||||||||
M1 |
|
|||||||||||||
L : |
|
x 4 |
|
y 1 |
z 2 |
. |
|
|
|
|||||
2 |
|
1 |
3 |
|
|
|
L |
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Решение. Воспользуемся результатом |
задачи 3.13. |
|
M2 |
|||||||||||
|
Рис. 3.11 |
|||||||||||||
Точка M1(2, 0, 1) |
проекция точки M0 на прямую L . |
|
||||||||||||
|
|
|||||||||||||
Координаты точки M 2 (x2, y2, z2 ) можно найти, используя соотношения: |
||||||||||||||
(x0 x2) 2 x1, ( y0 y2) 2 y1, (z0 z2) 2 z1 |
|
|||||||||||||
(рис. 3.11). Следовательно, |
|
|
|
|
|
|
|
|
||||||
x2 2x1 x0 4, |
y2 2 y1 y0 2, |
z2 2z1 z0 3. |
||||||||||||
Ответ: M 2 (4, 2, 3). |
|
|
|
|
|
|
|
|
||||||
29
Задача 3.15. Найти расстояние между параллельными прямыми
|
|
L : |
|
x 2 |
|
y 3 |
|
z 1 |
; |
L : |
x 5 |
|
y |
|
z 25 |
. |
|
||
|
|
1 |
3 |
2 |
|
2 |
2 |
3 |
2 |
|
2 |
|
|||||||
|
|
|
|
|
|
|
|||||||||||||
M1 |
L1 |
|
|
Решение. |
|
|
Нужно |
|
|
|
вычислить |
длину |
|||||||
s |
перпендикуляра d , |
опущенного из точки M1(2, 3, 1) , |
|||||||||||||||||
|
|
|
|||||||||||||||||
d |
|
|
через которую проходит прямая L1, на прямую L2 . Для |
||||||||||||||||
M2 |
s |
L2 |
этого построим параллелограмм со сторонами |
|
|||||||||||||||
|
M1M2 и |
||||||||||||||||||
Рис. 3.12 |
|
s (рис. 3.12). Здесь M 2 (5, 0, 25) – точка, через которую |
|||||||||||||||||
|
|
|
проходит прямая L2 , а s |
направляющий вектор пря- |
|||||||||||||||
мых (так как прямые параллельны, то s1 s2 s (3, 2, 2) ). Площадь S па-
раллелограмма вычисляется с помощью векторного произведения векторов |
|||||||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
M1M2 (3, 3, 24) и s(3, 2, 2) : |
|
|
|
|
|
|
|
k |
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
i |
|
j |
|
k |
|
|
|
|
|
|
i |
|
j |
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||||||||
M1M2 s |
3 |
3 |
24 |
3 |
|
1 |
1 |
8 |
|
3(18i 22 j 5k ), |
|||||||||||||||||||||
|
|
|
|
|
3 |
|
2 |
2 |
|
|
|
|
|
3 |
2 |
|
2 |
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
S |
M1M 2 |
|
3 |
|
324 484 25 3 |
833 . |
|
|
|||||||||||||||||||||
стороныРасстояние| s |d: |
получим, разделив площадь параллелограмма S на длину его |
||||||||||||||||||||||||||||||
| s | |
|
9 4 4 |
|
17, |
|
|
d S | s | 3 |
833 17 3 |
49 21. |
||||||||||||||||||||||
Ответ: d 21. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
Полезная формула. |
Если заданы две параллельные прямые (L1 || L2 ) |
||||||||||||||||||||||||||||||
L : |
|
x x1 |
|
y y1 |
|
z z1 |
; |
L : |
x x2 |
|
y y2 |
|
|
z z2 |
, |
||||||||||||||||
|
l |
|
|
|
|
|
|
|
|
||||||||||||||||||||||
1 |
|
|
|
|
|
m |
|
|
|
n |
|
|
|
|
2 |
|
l |
m |
|
n |
|||||||||||
то расстояние d между ними вычисляется по формуле |
|
|
|
|
|
||||||||||||||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
d |
|
M1M2 s |
, |
|
|
|
|
|
|
|
|
|
|||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
s |
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||
где M1(x1, y1, z1) и |
M2 (x2, |
y2, z2) точки, через которые проходят прямые |
|||||||||||||||||||||||||||||
L1 и L2 соответственно, |
s s1 |
s2 |
их направляющий вектор. |
||||||||||||||||||||||||||||
30
