sb000253

МИНОБРНАУКИ РОССИИ

–––––––––––––––––––––––––––––––––––––

Санкт-Петербургский государственный электротехнический университет «ЛЭТИ»

–––––––––––––––––––––––––––––––––––––

СИНТЕЗ ОПТИМАЛЬНОЙ СИСТЕМЫ УПРАВЛЕНИЯ

Методические указания к курсовому расчету

Санкт-Петербург Издательство СПбГЭТУ «ЛЭТИ»

2014

УДК 681.51. 681.3

Синтез оптимальной системы управления: методические указания к курсовому расчету / сост.: А. С. Ветчинкин, В. А. Зуев СПб.: Изд-во СПбГЭТУ

«ЛЭТИ», 2014. 24 с.

Содержат базовые теоретические сведения по процедурам проектирования оптимальных систем управления. Приведены практические рекомендации к построению оптимальных алгоритмов управления.

Предназначены для студентов, обучающихся по направлению 220400.68 «Управление в технических системах».

Утверждено редакционно-издательским советом университета

в качестве методических указаний

© СПбГЭТУ«ЛЭТИ», 2014

2

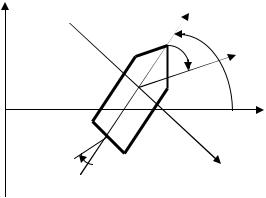
Курсовой расчет предназначен для ознакомления студентов с процессом проектирования алгоритма управления динамическим объектом на примере водоизмещающего судна.

Как известно [1], проектирование алгоритма управления состоит из следующих этапов:

1)математическое описание объекта управления;

2)математическая формулировка цели управления;

3)выбор метода решения поставленной оптимизационной задачи;

4)оценка вариантов решения задачи.

ОПИСАНИЕ ОБЪЕКТА УПРАВЛЕНИЯ

Динамика судна, как и любого физического тела, подчиняется второму закону Ньютона. Силы и моменты, действующие на судно, в свою очередь, описываются законами гидродинамики. Соотношения между кинематическими параметрами движения ( φ – угол рыскания, ωy – угловая скорость

рыскания, β – угол дрейфа, δ – угол перекладки руля, v – линейная скорость судна) показаны на рис. 1.

δ

Рис. 1

В общем случае зависимость сил и моментов, действующих на судно, от параметров движения носит нелинейный характер. Однако предположение о малых значениях угла дрейфа и угловой скорости рыскания и постоянстве линейной скорости движения судна позволяют линеаризовать эти зависимости. При этом динамика судна будет описываться системой линейных дифференциальных уравнений относительно углов рыскания, дрейфа, угловой скорости рыскания, угла перекладки руля и одного нелинейного соотношения, отражающего тот факт, что руль не может поворачиваться на произ-

3

вольный угол при произвольном сигнале управления. Для большинства современных судов максимальный угол перекладки руля равен 35°. Упомянутые соотношения, записанные относительно нормированного времени (τ) , имеют вид:

b11 = −s31Ω2, b21 = −s21Ω.

Значение нормирующей частоты Ω = vL0 вычисляется по данным прил. 1,

содержащего варианты параметров математических моделей судов.

МАТЕМАТИЧЕСКАЯ ФОРМУЛИРОВКА ЦЕЛИ УПРАВЛЕНИЯ

При выполнении настоящей курсовой работы требуется спроектировать алгоритм управления рулем судна, который обеспечивает минимальное время выполнения устранения начального значения рассогласования по углу рыскания 10°.

Другими словами, требуется спроектировать оптимальный по быстродействию алгоритм выполнения градусной поправки 10°.

4

ВЫБОР МЕТОДА РЕШЕНИЯ ОПТИМИЗАЦИОННОЙ ЗАДАЧИ

В рамках настоящего курсового расчета студентам предлагается выполнить проектирование алгоритма управления тремя методами (двумя прямыми и одним из двух косвенных).

Прямые методы:

∙метод, основанным на теореме об N интервалах,

∙метод параметрической оптимизации линейного закона управления. Косвенные методы:

∙минимизация интегрального квадратичного функционала,

∙метод стандартного полинома.

Метод, основанный на теореме об N интервалах, заключается в определении (N–1)- го момента переключения знака управляющего воз-действия и момента выключения управления, таких, которые обеспечивают перевод

судна из начального ( φ = 10 , β = 0 , ωy = 0 ) в конечное ( φ = 0 , β = 0 , ωy = 0 ) состояние к моменту времени выключения управления, где N – поря-док дифференциального уравнения (или системы уравнений), описывающего объект управления.

В рассматриваемом случае теорема об N интервалах применима, так как система уравнений, описывающих судно, имеет вещественные корни.

Задачу определения моментов переключения (t1, t2) и момента выключения (T ) предлагается решать поисковым методом.

Для реализации поиска целесообразно использовать функцию FMINSEARCH из пакета MATLAB.

При выполнении расчетов необходимо учесть, что поисковые методы не могут обеспечить точное решение за конечное количество шагов. В связи с этим целесообразно смягчить поставленную задачу, потребовав минимизировать отклонение состояния объекта от требуемого в момент выключения управления.

Известно, что результат, получаемый с помощью поисковых методов, может существенно зависеть от выбора начальной точки поиска. В связи с этим при проектировании алгоритма управления на основании теоремы об N интервалах рекомендуется выполнять мероприятия, направленные на определение начальной комбинации искомых параметров.

5

Поскольку уравнения по угловой скорости рыскания и углу дрейфа для рассматриваемого объекта управления не зависят от угла рыскания, то первое приближение для набора искомых параметров можно определить с помощью решения промежуточной задачи пониженного порядка.

В качестве промежуточной удобно рассмотреть задачу перевода судна из состояния ωy = 0 , β = 0 в состояние ωy = 0 , β = 0 за счет выполнения двух

переключений знака угла перекладки руля.

При выборе произвольного значения для первого момента переключения соответствующие значения для второго момента переключения и момента выключения могут быть определены графическим методом на основе построения линии переключения в плоскости ωyβ . В результате решения про-

межуточной задачи определяется набор параметров (t1, t2, T ) , которые соответствуют переводу судна из заданного начального состояния в состояние промежуточного финиша φ(T ) = φ f , которое отличается от заданного конеч-

ного состояния φ(T ) = 0 . Определение окончательного набора параметров может быть организовано в виде итеративной процедуры поиска

минимума функции Ji = (φ(T ) − φ fi )2 + ω2y + β2 .

На каждом шаге итеративной процедуры в качестве начального набора параметров (t1, t2, T ) при поиске функции минимума Ji используется результат предыдущего шага, а значение φ fi систематически приближается к за-

данному конечному значению угла рыскания φ(T ) = 0 .

В качестве примера применения теоремы об N интервалах рассмотрим задачу, приведенную в прил. 4.

Метод параметрической оптимизации линейного закона управления заключается в поиске таких значений параметров линейного закона управления, которые обеспечивают перевод объекта управления в заданное состояние за минимальное время и последующее удержание объекта в этом состоянии.

Одним из достоинств этого метода является возможность включения в закон управления только тех переменных состояния, которые соответствуют достаточно точно измеряемым физическим величинам. В случае водоизмещающего судна наиболее точно из принятых в рассмотрение физических величин измеряются угол рыскания и угловая скорость рыскания.

6

С математической точки зрения задача параметрической оптимизации заключается в том, чтобы для алгоритма управления δ = −K1φ − K2ωy найти

такие значения параметров K1 и K2 , при которых время перевода судна из начальной точки в конечную минимально.

Поскольку в рассматриваемом случае изменение состояния судна вблизи целевой точки носит экспоненциальный характер, то теоретически время перехода в целевое состояние не ограничено. В связи с этим предлагается принимать за окончание процесса управления момент времени, после которого абсолютное значение угла рыскания не превышает 5 % от начального значения.

Очевидно, что для решения этой задачи удобно использовать MATLABфункцию FMINSEARCH, которая возвращает искомые значения параметров алгоритма управления в виде вектора, а в процессе поиска вызывает процедуру определения времени переходного процесса, соответствующего текущим значениям искомых параметров. В свою очередь, реализация процедуры определения времени переходного процесса может быть основана на применении MATLAB-функции ODE45, обеспечивающей получение решения дифференциальных уравнений замкнутой системы управления в виде массива значений φ(t) . Кроме вызова функции ODE45 для определения длительности переходного процесса необходимо выполнить обработку массива значений φ(t) . Пример решения задачи параметрической оптимизации при-

веден в прил. 5.

Минимизация интегрального квадратичного функционала

∞

J = ∫ (λφ2 + δ2)dt

0

в общем случае не эквивалентна минимизации времени переходного процесса. Однако можно показать, что переходные процессы в системах, оптимальных по интегральным квадратичным функционалам, ускоряются при увеличении значений весовых множителей. Следовательно, можно приблизиться к задаче максимального быстродействия, решив задачу поиска такого весового множителя, при котором практическое время переходного процесса имеет минимальное значение.

Для вычисления параметров алгоритма управления целесообразно использовать MATLAB-функцию LQR.

7

В том случае, когда объект управления описывается линейным матричным дифференциальным уравнением, имеющим вид

dX = AX + BU, dt

где X – вектор состояния объекта управления; U – вектор управляющих воздействий, а функционал качества имеет вид:

J = ∞∫(XТQX + UТRU)dt.

0

где Q и R – весовые матрицы, и алгоритм управления имеет вид:

U = KX,

где: K – искомая матрица параметров алгоритма управления, которая вычисляется путем выполнения следующей строки MATLAB-скрипта:

K = lqr (A, B, Q, R).

Общий алгоритм решения задачи синтеза алгоритма управления, основанный на минимизации квадратичного функционала, является процедурой одномерного поиска значения весового множителя и может быть реализован с помощью MATLAB-функции FMINSEARCH.

Для обеспечения решения задачи FMINSEARCH должна ссылаться на функцию, которая по заданному значению весового множителя определяет время переходного процесса. Для его вычисления первоначально с помощью LQR определяются параметры линейного алгоритма управления, соответствующие текущему значению весового множителя, затем формируется математическая модель замкнутой системы и с помощью ODE45 выполняется расчет массива значений, соответствующих переходному процессу по углу рыскания. Искомое значение времени переходного процесса определяется на основе обработки массива значений угла рыскания.

Стоит отметить следующее: на этапе вычисления параметров алгоритма управления предполагается, что движение судна полностью описывается линейными уравнениями, а на этапе вычисления времени переходного процесса учитывается ограничение на значение перекладки руля.

Пример решения линейной квадратичной задачи оптимизации приведен в прил. 6.

Подобно минимизации интегрального квадратичного функционала задача назначения заданного расположения собственных чисел системы управления (задача модального управления) не эквивалентна задаче макси-мального быстродействия. Однако и в этом случае возможно приближение к основной

8

задаче за счет поиска соответствующего значения нормирующей частоты выбранного стандартного полинома.

Таким образом, задача модального управления рассматривается как задача поиска такого значения нормирующей частоты выбранного стандартного полинома, которое соответствует минимуму времени переходного процесса по углу рыскания (задача одномерной оптимизации) и может быть решена с помощью MATLAB-функции FMINSEARCH.

Для решения задачи FMINSEARCH должна ссылаться на функцию, которая вычисляет время переходного процесса, соответствующее текущему значению нормирующей частоты стандартного полинома. Для вычисления времени переходного процесса первоначально вычисляются коэффициенты стандартного полинома, соответствующие текущему значению нормирующей частоты. Затем вычисляются корни полученного полинома, которые рассматриваются в дальнейшем как желаемые корни замкнутой системы управления. Операция вычисления корней может быть выполнена с помощью MATLAB-функции ROOTS. Затем по известной математической модели объекта управления и желаемым корням характеристического уравнения замкнутой системы вычисляются параметры линейного алгоритма управления. Последняя операция может быть выполнена с помощью MATLAB-функции ACKER. На последнем этапе с помощью ODE45 вычисляется массив значений угла рыскания и с помощью обработки массива значений угла рыскания

– время переходного процесса.

Пример решения задачи модального управления приведен в прил. 7. Поскольку задача проектирования решается относительно прибли-

женной математической модели объекта управления, представляется целесообразным проанализировать чувствительность полученных различными методами алгоритмов управления к изменению параметров объекта управления. Эту операцию предлагается выполнить методом моделирования.

Последним этапом курсового расчета является выбор одного из полученных алгоритмов для практической реализации с помощью сравнения по следующим показателям:

∙степень достижения поставленной цели (время переходного процесса);

∙сложность задач, решаемых на этапе проектирования;

∙сложность реализации алгоритма управления;

9

∙ чувствительность основного показателя качества (времени переходного процесса) к изменению параметров математической модели объекта управления.

Список литературы

Лукомский Ю. А., Корчанов В. М. Управление морскими подвижными объектами: учеб. СПб.: Элмор, 1996. 320 с.; ил.

10